(北师大版)2022-2023学年度第一学期七年级数学1.3 截一个几何体 同步测试
试卷更新日期:2022-07-10 类型:同步测试
一、单选题
-
1. 如图,用一个平面去截圆锥,得到的截面是( )
 A、
A、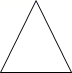 B、
B、 C、
C、 D、
D、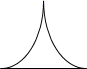 2. 用一个平面去截一个几何体,若截面的形状是长方形,则原来的几何体不可能是( )A、正方体 B、直棱柱 C、圆柱 D、圆锥3. 用一个平面去截一个几何体,截面可能都是圆的几何体是( )A、球、棱柱 B、球、圆锥、圆柱 C、球、正方体 D、圆锥、棱柱4. 用刀子去截一块长方体形的豆腐块,截面的形状不可能是( )A、四边形 B、五边形 C、六边形 D、七边形5. 用一平面去截下列几何体,其截面可能是长方形的有( )
2. 用一个平面去截一个几何体,若截面的形状是长方形,则原来的几何体不可能是( )A、正方体 B、直棱柱 C、圆柱 D、圆锥3. 用一个平面去截一个几何体,截面可能都是圆的几何体是( )A、球、棱柱 B、球、圆锥、圆柱 C、球、正方体 D、圆锥、棱柱4. 用刀子去截一块长方体形的豆腐块,截面的形状不可能是( )A、四边形 B、五边形 C、六边形 D、七边形5. 用一平面去截下列几何体,其截面可能是长方形的有( )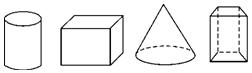 A、1个 B、2个 C、3个 D、4个6. 用平面去截正方体,在所得的截面中,边数最多的截面是( )A、六边形 B、五边形 C、四边形 D、三角形7. 如图,是将一个长方体截去一个角后所得的几何体,该几何体棱的条数共有( )
A、1个 B、2个 C、3个 D、4个6. 用平面去截正方体,在所得的截面中,边数最多的截面是( )A、六边形 B、五边形 C、四边形 D、三角形7. 如图,是将一个长方体截去一个角后所得的几何体,该几何体棱的条数共有( ) A、11 B、12 C、13 D、148. 如图是一个正方体,小敏同学经过研究得到如下5个结论,正确的结论有( )个.
A、11 B、12 C、13 D、148. 如图是一个正方体,小敏同学经过研究得到如下5个结论,正确的结论有( )个.①用剪刀沿着它的棱剪开这个纸盒,至少要剪7刀,才能展开成平面图形;②用一平面去截这个正方体得到的截面是三角形ABC,则∠ABC=45°;③一只蚂蚁在一个实心正方体木块P点处想沿着表面爬到C点最近的路只有4条;④用一平面去截这个正方体得到的截面可能是八边形;⑤正方体平面展开图有11种不同的图形.
 A、1 B、2 C、3 D、49. 下列说法,不正确的是( )A、用一个平面去截长方体,截面可能是正方形 B、用一个平面去截正方体,截面可能是等腰梯形 C、用一个平面去截圆锥,截面可能是梯形 D、用一个平面去截正方体,截面可能是等边三角形10. 如图,一个有盖的圆柱形玻璃杯中装有半杯水,若任意放置这个水杯,则水面的形状不可能是( )
A、1 B、2 C、3 D、49. 下列说法,不正确的是( )A、用一个平面去截长方体,截面可能是正方形 B、用一个平面去截正方体,截面可能是等腰梯形 C、用一个平面去截圆锥,截面可能是梯形 D、用一个平面去截正方体,截面可能是等边三角形10. 如图,一个有盖的圆柱形玻璃杯中装有半杯水,若任意放置这个水杯,则水面的形状不可能是( )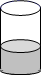 A、
A、 B、
B、 C、
C、 D、
D、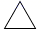
二、填空题
-
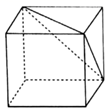
11. 如图,一个正方体截去一个角后,剩下的几何体有条棱.
 12. 用一个平面去截一个正方体,得到的截面的形状可能是:①圆,②三角形,③长方形,④五边形,⑤六边形,⑥七边形其中的 .13. 下列几何体:①圆柱;②正方体;③棱柱;④球;在这些几何体中截面可能是圆的有 . (只填写序号即可)14. 用不同的方法将长方体截去一个角,在剩下的几何体中,最少有个顶点.15. 用一个平面截一个几何体,所截出的面出现了如图所示的四种形式,试猜想,该几何体可能是 .
12. 用一个平面去截一个正方体,得到的截面的形状可能是:①圆,②三角形,③长方形,④五边形,⑤六边形,⑥七边形其中的 .13. 下列几何体:①圆柱;②正方体;③棱柱;④球;在这些几何体中截面可能是圆的有 . (只填写序号即可)14. 用不同的方法将长方体截去一个角,在剩下的几何体中,最少有个顶点.15. 用一个平面截一个几何体,所截出的面出现了如图所示的四种形式,试猜想,该几何体可能是 .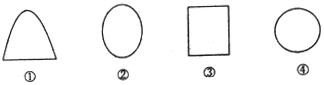
三、解答题
-
16. 分别指出图中几何体的截面形状的标号:
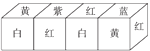
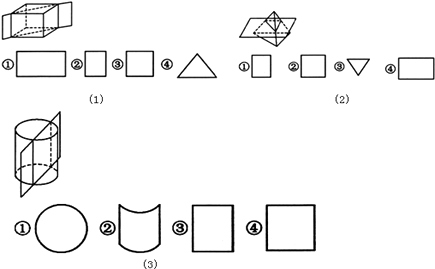 (1)、中截面形状的标号:;(2)、中截面形状的标号:;(3)、中截面形状的标号: .17. 把正方体的六个面分别涂上六种不同的颜色,并画上朵数不等的花,各面上的颜色与花的朵数情况见下表:
(1)、中截面形状的标号:;(2)、中截面形状的标号:;(3)、中截面形状的标号: .17. 把正方体的六个面分别涂上六种不同的颜色,并画上朵数不等的花,各面上的颜色与花的朵数情况见下表:颜色
红
黄
蓝
白
紫
绿
花的朵数
1
2
3
4
5
6
现将上述大小相同,颜色.花朵分布也完全相同的四个正方体拼成一个水平放置的长方体,如图所示.问:长方体的下底面共有多少朵花?
 18. 如图所示,一个长方体的长.宽.高分别是 10cm,8cm,6cm,有一只蚂蚁从点 A 出发沿棱爬行,每条棱不允许重复,则蚂蚁回到点 A 时,最多爬行多远?并把蚂蚁所爬行的路线用字母按顺序表示出来.
18. 如图所示,一个长方体的长.宽.高分别是 10cm,8cm,6cm,有一只蚂蚁从点 A 出发沿棱爬行,每条棱不允许重复,则蚂蚁回到点 A 时,最多爬行多远?并把蚂蚁所爬行的路线用字母按顺序表示出来.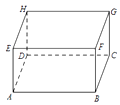 19. 如图所示的正方体被竖直截取了一部分,求被截取的那一部分的体积.(棱柱的体积等于底面积乘高)
19. 如图所示的正方体被竖直截取了一部分,求被截取的那一部分的体积.(棱柱的体积等于底面积乘高)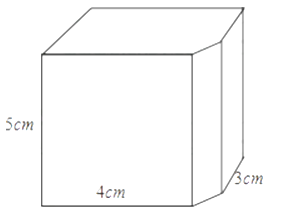 20.
20.将如图中几何体的截面用阴影部分表示出来,并分别指出它们的形状.
 21. 如图所示的正方体被竖直截取了一部分,求被截取的那一部分的体积.(棱柱的体积等于底面积乘高)
21. 如图所示的正方体被竖直截取了一部分,求被截取的那一部分的体积.(棱柱的体积等于底面积乘高) 22.
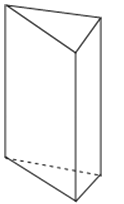
22.如图所示的是一个三棱柱,用一个平面先后三次截这个三棱柱.
(1)截得的截面能否是三个与该三棱柱的底面大小相同的三角形?若能,画图说明你的截法.
(2)截得的截面能否是三个长相等的长方形?若能,画图说明你的截法;
(3)截得的截面能否是梯形?若能.画图说明你的一种截法.
 23. 如图①,从大正方体上截去一个小正方体之后,可以得到图②的几何体.
23. 如图①,从大正方体上截去一个小正方体之后,可以得到图②的几何体.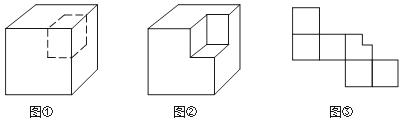
(1)设原大正方体的表面积为S,图②中几何体的表面积为S1 , 那么S1与S的大小关系是
A.S1>S B.S1=S C.S1<S D.无法确定
(2)小明说:“设图①中大正方体各棱的长度之和为l,图②中几何体各棱的长度之和为l1 , 那么l1比l正好多出大正方体3条棱的长度.”你认为这句话对吗?为什么?
(3)如果截去的小正方体的棱长为大正方体棱长的一半,那么图③是图②中几何体的表面展开图吗?如有错误,请予修正.