(人教版)2022-2023学年度第一学期九年级数学第22章 二次函数 单元测试
试卷更新日期:2022-07-08 类型:单元试卷
一、单选题
-
1. 下列函数中是二次函数的是( )A、 B、 C、 D、2. 用长为2米的绳子围成一个矩形,它的一边长为x米,设它的面积为S平方米,则S与x的函数关系为( )A、正比例函数关系 B、反比例函数关系 C、一次函数关系 D、二次函数关系3. 设A( , ),B( , ),C(3, )是抛物线 上的三点,则 , , 的大小关系为( )A、 B、 C、 D、4. 二次函数y=3(x-1)2+2图象的顶点坐标是( )A、(2,1) B、(-2,-1) C、(-1,2) D、(1,2)5. 抛物线 共有的性质是( )A、开口向上 B、都有最高点 C、对称轴是 轴 D、 随 的增大而减小6. 二次函数y=﹣x²-3x+1的图象的顶点在( )A、第四象限 B、第三象限 C、第二象限 D、第一象限7. 对于二次函数y=x2 4x 1的图象,下列叙述正确的是( )A、开口向下 B、对称轴为直线x=2 C、顶点坐标为( 2, 5) D、当x≥2时,y随x增大而减小8. 抛物线y=ax2+bx+c(a≠0)的部分图象如图所示,关于x的一元二次方程ax2+bx+c=0的解分别为x1 , x2 , 则x1+x2的值为( )
 A、2 B、1 C、﹣1 D、﹣29. 已知二次函数与轴的交点是(1,0)和(3,0),关于的方程(其中)的两个解分别是和5,关于的方程(其中)也有两个整数解,这两个整数解分别是( )A、1和4 B、2和5 C、0和4 D、0和510. 如图,四边形ABCD中,AB=AD , CE⊥BD , CE= BD . 若△ABD的周长为20cm,则△BCD的面积S(cm2)与AB的长x(cm)之间的函数关系式可以是( )
A、2 B、1 C、﹣1 D、﹣29. 已知二次函数与轴的交点是(1,0)和(3,0),关于的方程(其中)的两个解分别是和5,关于的方程(其中)也有两个整数解,这两个整数解分别是( )A、1和4 B、2和5 C、0和4 D、0和510. 如图,四边形ABCD中,AB=AD , CE⊥BD , CE= BD . 若△ABD的周长为20cm,则△BCD的面积S(cm2)与AB的长x(cm)之间的函数关系式可以是( )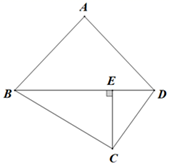 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
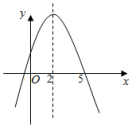
11. 若二次函数y=2x2-3的图象上有两个点A(1,m),B(2,n),则mn(填“<”“=”或“>”).12. 如果抛物线的对称轴是轴,那么顶点坐标为13. 如果抛物线的顶点在轴上,那么常数m的值是14. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则关于x的方程ax2+bx+c=0(a≠0)的解为 .
 15. 某件商品的销售利润y(元)与商品销售单价x(元)之间满足 , 不考虑其他因素,销售一件该商品的最大利润为元.
15. 某件商品的销售利润y(元)与商品销售单价x(元)之间满足 , 不考虑其他因素,销售一件该商品的最大利润为元.三、解答题
-
16. 若函数y=(a-1)x(b+1)+x2+1是二次函数,试讨论a、b的取值范围。
17. 在同一坐标系中,画出函数y1=2x2 , y2=2(x-2)2与y3=2(x+2)2的图象,并说明y2 , y3的图象与y1=2x2的图象的关系.18. 用配方法把二次函数 化为 的形式,再指出该函数图象的开口方向、对称轴和顶点坐标.19. 把抛物线y=ax2+bx+c先向右平移3个单位长度,再向下平移2个单位长度,所得抛物线是y=x2﹣3x+5,求a+b+c的值.20. 用配方法把二次函数y= x2﹣4x+5化为y=a(x﹣m)2+k的形式,并写出该函数图象的顶点坐标.21. 已知二次函数y=kx2﹣2x﹣1的图像与x轴有两个不同的交点,求实数k的取值范围.
