(人教版)2022-2023学年度第一学期九年级数学22.3 实际问题与二次函数 同步测试
试卷更新日期:2022-07-08 类型:同步测试
一、单选题
-
1. 拱桥的形状是抛物线,其函数关系式为 , 当水面离桥顶的高度为m时,水面的宽度为( )米.
 A、8 B、9 C、10 D、112. 竖直向上发射的小球的高度关于运动时间的函数表达式为 , 其图象如图所示,若小球发射后第2秒与第6秒时的高度相等,则下列时刻中小球的高度最高的是( )
A、8 B、9 C、10 D、112. 竖直向上发射的小球的高度关于运动时间的函数表达式为 , 其图象如图所示,若小球发射后第2秒与第6秒时的高度相等,则下列时刻中小球的高度最高的是( ) A、第3秒 B、第3.5秒 C、第4秒 D、第4.5秒3. 一位运动员在离篮筐水平距离4m处起跳投篮,球运行路线可看作抛物线,当球离开运动员的水平距离为1m时,它与篮筐同高,球运行中的最大高度为3.5m,最后准确落入篮筐,已知篮筐到地面的距离为3.05m,该运动员投篮出手点距离地面的高度为( )
A、第3秒 B、第3.5秒 C、第4秒 D、第4.5秒3. 一位运动员在离篮筐水平距离4m处起跳投篮,球运行路线可看作抛物线,当球离开运动员的水平距离为1m时,它与篮筐同高,球运行中的最大高度为3.5m,最后准确落入篮筐,已知篮筐到地面的距离为3.05m,该运动员投篮出手点距离地面的高度为( ) A、1.5m B、2m C、2.25m D、2.5m4. 如图所示,一座抛物线形的拱桥在正常水位时,水而AB宽为20米,拱桥的最高点O到水面AB的距离为4米.如果此时水位上升3米就达到警戒水位CD,那么CD宽为( )
A、1.5m B、2m C、2.25m D、2.5m4. 如图所示,一座抛物线形的拱桥在正常水位时,水而AB宽为20米,拱桥的最高点O到水面AB的距离为4米.如果此时水位上升3米就达到警戒水位CD,那么CD宽为( ) A、米 B、10米 C、米 D、12米5. 如图,一个矩形的长比宽多3cm,矩形的面积是Scm2 . 设矩形的宽为xcm,当x在一定范围内变化时,S随x的变化而变化,则S与x满足的函数关系是( )
A、米 B、10米 C、米 D、12米5. 如图,一个矩形的长比宽多3cm,矩形的面积是Scm2 . 设矩形的宽为xcm,当x在一定范围内变化时,S随x的变化而变化,则S与x满足的函数关系是( ) A、S=4x+6 B、S=4x-6 C、S=x2+3x D、S=x2-3x6. 一个球从地面竖直向上弹起时的速度为8米/秒,经过t秒时球的高度为h米,h和t满足公式:
A、S=4x+6 B、S=4x-6 C、S=x2+3x D、S=x2-3x6. 一个球从地面竖直向上弹起时的速度为8米/秒,经过t秒时球的高度为h米,h和t满足公式: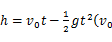 表示球弹起时的速度,g表示重力系数,取 米/秒 ,则球不低于3米的持续时间是( ) A、 秒 B、 秒 C、 秒 D、1秒7. 竖直向上发射的小球的高度 关于运动时间 的函数表达式为 ,其图象如图所示,若小球发射后第2秒与第6秒时的高度相等,则下列时刻中小球的高度最高的是( )
表示球弹起时的速度,g表示重力系数,取 米/秒 ,则球不低于3米的持续时间是( ) A、 秒 B、 秒 C、 秒 D、1秒7. 竖直向上发射的小球的高度 关于运动时间 的函数表达式为 ,其图象如图所示,若小球发射后第2秒与第6秒时的高度相等,则下列时刻中小球的高度最高的是( ) A、第3秒 B、第3.5秒 C、第4秒 D、第6秒8. 如图,要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管的长为( )
A、第3秒 B、第3.5秒 C、第4秒 D、第6秒8. 如图,要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管的长为( ) A、 B、 C、 D、9. 如图,在中, , , , 动点从点开始沿边向以的速度移动(不与点重合),动点从点开始沿边向以的速度移动(不与点重合).如果、分别从、同时出发,那么经过( )秒,四边形的面积最小.
A、 B、 C、 D、9. 如图,在中, , , , 动点从点开始沿边向以的速度移动(不与点重合),动点从点开始沿边向以的速度移动(不与点重合).如果、分别从、同时出发,那么经过( )秒,四边形的面积最小. A、0.5 B、1.5 C、3 D、410. 某种商品的价格是 元,准备进行两次降价.如果每次降价的百分率都是 ,经过两次降价后的价格 (单位:元)随每次降价的百分率 的变化而变化,则 关于 的函数解析式是( )A、 B、 C、 D、
A、0.5 B、1.5 C、3 D、410. 某种商品的价格是 元,准备进行两次降价.如果每次降价的百分率都是 ,经过两次降价后的价格 (单位:元)随每次降价的百分率 的变化而变化,则 关于 的函数解析式是( )A、 B、 C、 D、二、填空题
-
11. 用长12m的铝合金条制成矩形窗框(如图所示),那么这个窗户的最大透光面积是(中间横框所占的面积忽略不计)
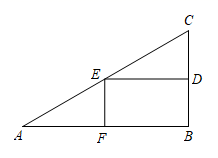
 12. 如图,在矩形 ABCD 中,AD=3,点E是AD边上的动点,连结CE,以CE为边向右上方作正方形CEFG,过点F作 FH⊥AD,垂足为H,连结AF. 在整个变化过程中,△AEF 面积的最大值是 .
12. 如图,在矩形 ABCD 中,AD=3,点E是AD边上的动点,连结CE,以CE为边向右上方作正方形CEFG,过点F作 FH⊥AD,垂足为H,连结AF. 在整个变化过程中,△AEF 面积的最大值是 . 13. 中国跳水队在第三十二届夏季奥林匹克运动会上获得7金5银12枚奖牌的好成绩.某跳水运动员从起跳至人水的运动路线可以看作是抛物线的一部分.如图所示,该运动员起跳点A距离水面10m,运动过程中的最高点B距池边2.5m,入水点C距池边4m,根据上述信息,可推断出点B距离水面m.
13. 中国跳水队在第三十二届夏季奥林匹克运动会上获得7金5银12枚奖牌的好成绩.某跳水运动员从起跳至人水的运动路线可以看作是抛物线的一部分.如图所示,该运动员起跳点A距离水面10m,运动过程中的最高点B距池边2.5m,入水点C距池边4m,根据上述信息,可推断出点B距离水面m.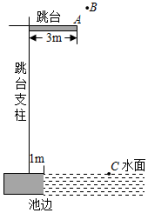 14. 据了解,某蔬菜种植基地2019年的蔬菜产量为100万吨,2021年的蔬菜产量为万吨,如果2019年至2021年蔬菜产量的年平均增长率为 , 那么y关于x的函数解析式为 .15. 如图,有一矩形养鸡场,养鸡场的一边靠墙(墙足够长),另三边用米的长篱笆围成,则矩形面积的最大值是平方米.
14. 据了解,某蔬菜种植基地2019年的蔬菜产量为100万吨,2021年的蔬菜产量为万吨,如果2019年至2021年蔬菜产量的年平均增长率为 , 那么y关于x的函数解析式为 .15. 如图,有一矩形养鸡场,养鸡场的一边靠墙(墙足够长),另三边用米的长篱笆围成,则矩形面积的最大值是平方米.
三、解答题
-
16. 如图,人工喷泉有一个竖直的喷水枪AB,喷水口A距地面2.25m,喷泉水流的运动路线是抛物线,水流的最高点P到喷水枪AB所在直线的距离为1m,且到地面的距离为3m,以B点为原点,地面水平线和AB所在的直线为x,y轴建立平面直角坐标系,求水流的落地点C到水枪底部B的距离.
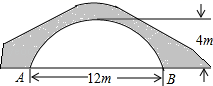
 17. 如图是抛物线形拱桥,当水面宽为4米时,拱顶距离水面2米;当水面高度下降1米时,水面宽度为多少米?请你以点D为原点、 所在直线为x轴建立平面直角坐标系,解决这个实际问题.
17. 如图是抛物线形拱桥,当水面宽为4米时,拱顶距离水面2米;当水面高度下降1米时,水面宽度为多少米?请你以点D为原点、 所在直线为x轴建立平面直角坐标系,解决这个实际问题. 18. 如图,矩形绿地的长、宽各增加 ,写出扩充后的绿地的面积y与x的关系式.
18. 如图,矩形绿地的长、宽各增加 ,写出扩充后的绿地的面积y与x的关系式. 19. 在体育课掷实心球活动中,小华通过研究发现:实心球所经过的路线是一条抛物线的一部分,如果球出手处点 距离地面的高度为 ,当球运行的水平距离为 时,达到最大高度 的 处(如图),问实心球的落地点 与出手处点 的水平距离是多少?(结果保留根号)
19. 在体育课掷实心球活动中,小华通过研究发现:实心球所经过的路线是一条抛物线的一部分,如果球出手处点 距离地面的高度为 ,当球运行的水平距离为 时,达到最大高度 的 处(如图),问实心球的落地点 与出手处点 的水平距离是多少?(结果保留根号) 20. 某民俗旅游村为接待游客住宿需要,开设了有100张床位的旅馆,当每张床位每天收费80元时,床位可全部租出,若每张床位每天收费提高10元,则相应的减少了10张床位租出,如果每张床位每天以10元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天应提高多少元?21. 某幢建筑物,从5米高的窗口 用水管向外喷水,喷出的水呈抛物线状(抛物线所在的平面与墙面垂直,如图所示),如果抛物线的最高点 离墙1米,此时高度为10米.如图,在所示的平面直角坐标系中,求水流落地点 离墙距离 .(结果保留根号)
20. 某民俗旅游村为接待游客住宿需要,开设了有100张床位的旅馆,当每张床位每天收费80元时,床位可全部租出,若每张床位每天收费提高10元,则相应的减少了10张床位租出,如果每张床位每天以10元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天应提高多少元?21. 某幢建筑物,从5米高的窗口 用水管向外喷水,喷出的水呈抛物线状(抛物线所在的平面与墙面垂直,如图所示),如果抛物线的最高点 离墙1米,此时高度为10米.如图,在所示的平面直角坐标系中,求水流落地点 离墙距离 .(结果保留根号)