(人教版)2022-2023学年度第一学期九年级数学22.2 二次函数与一元二次方程 同步测试
试卷更新日期:2022-07-08 类型:同步测试
一、单选题
-
1. 已知函数 的对称轴为直线 .若 是方程 的两个根,且 ,则下列说法正确的是( )
 A、 B、 C、 D、2. “如果二次函数 的图像与 轴有两个交点,那么一元二次方程 有两个不相等的实数根.”请根据这句话的理解,解决以下问题;若 、 是关于 的方程 的两根,且 ,则 , , , 的大小关关系是( )A、 B、 C、 D、3. 在二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表,则方程ax2+bx+c=0的一个解x的范围是( )
A、 B、 C、 D、2. “如果二次函数 的图像与 轴有两个交点,那么一元二次方程 有两个不相等的实数根.”请根据这句话的理解,解决以下问题;若 、 是关于 的方程 的两根,且 ,则 , , , 的大小关关系是( )A、 B、 C、 D、3. 在二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表,则方程ax2+bx+c=0的一个解x的范围是( )x
…
1
1.1
1.2
1.3
1.4
…
y
…
1
0.49
0.04
0.59
1.16
…
A、1<x<1.1 B、1.1<x<1.2 C、1.2<x<1.3 D、1.3<x<1.44. 已知一元二次方程2x2+bx 1=0的一个根是1,若二次函数y=2x2+bx 1的图象上有三个点(0,y1)、( 1,y2)、( y3),则y1 , y2 , y3的大小关系为( )A、y1<y2<y3 B、y2<y1<y3 C、y1<y3<y2 D、y3<y1<y25. 根据以下表格中二次函数y=ax2+bx+c的自变量x与函数值y的对应值,可以判断方程ax2+bx+c=0的一个解x的范围是( )x
0
0.5
1
1.5
2
y=ax2+bx+c
-1
-0.5
1
3.5
7
A、0<x<0.5 B、0.5<x<1 C、1<x<1.5 D、1.5<x<26. 在求解方程时,先在平面直角坐标系中画出函数的图象,观察图象与x轴的两个交点,这两个交点的横坐标可以看作是方程的近似解,分析右图中的信息,方程的近似解是( ) A、 , B、 , C、 , D、 ,7. 二次函数图象经过点 , 且图象对称轴为直线 , 则方程的解为( )A、 B、 , C、 , D、 ,8. 如图,二次函数y=ax2+bx+c(a<0)的图象经过原点O,与x轴另一个交点为A点,则方程ax2+bx+c=0的解是( )
A、 , B、 , C、 , D、 ,7. 二次函数图象经过点 , 且图象对称轴为直线 , 则方程的解为( )A、 B、 , C、 , D、 ,8. 如图,二次函数y=ax2+bx+c(a<0)的图象经过原点O,与x轴另一个交点为A点,则方程ax2+bx+c=0的解是( )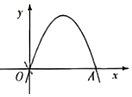 A、两个正根 B、两个负根 C、一个正根,一个负根 D、0和一个正根9. 若二次函数的对称轴是x=4,则关于x的方程的解为( )A、x1=0,x2=8 B、x1=1,x2=9 C、x1=1,x2=﹣9 D、x1=﹣1,x2=910. 已知抛物线在平面直角坐标系中的位置如图,则下列结论中正确的是( )
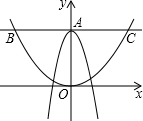
A、两个正根 B、两个负根 C、一个正根,一个负根 D、0和一个正根9. 若二次函数的对称轴是x=4,则关于x的方程的解为( )A、x1=0,x2=8 B、x1=1,x2=9 C、x1=1,x2=﹣9 D、x1=﹣1,x2=910. 已知抛物线在平面直角坐标系中的位置如图,则下列结论中正确的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 已知二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,则关于x的一元二次方程ax2+bx+c=0的解为 .
 12. 如图,将二次函数(其中)的图象在轴下方的部分沿轴翻折,图象的其余部分保持不变,形成新的图象记为 , 另有一次函数的图象记为 , 若与恰有两个交点时,则的范围是.
12. 如图,将二次函数(其中)的图象在轴下方的部分沿轴翻折,图象的其余部分保持不变,形成新的图象记为 , 另有一次函数的图象记为 , 若与恰有两个交点时,则的范围是. 13. 二次函数y=ax2+bx+4的图象如图所示,则关于x的方程a(x+1)2+b(x+1)=﹣4的根为 .
13. 二次函数y=ax2+bx+4的图象如图所示,则关于x的方程a(x+1)2+b(x+1)=﹣4的根为 .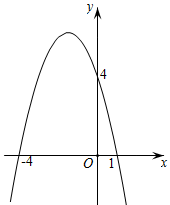 14. 若关于x的一元二次方程 (t为实数)在 的范围内有解,则t的取值范围是 .15. 已知抛物线 的图像与x轴分别交于点 , ,则关于x的方程 的根为 .
14. 若关于x的一元二次方程 (t为实数)在 的范围内有解,则t的取值范围是 .15. 已知抛物线 的图像与x轴分别交于点 , ,则关于x的方程 的根为 .三、解答题
-
16. 若二次函数的对称轴为直线 , 求关于x的方程的解.17. 二次函数y=x2﹣2x﹣3的图象与x轴交于A、B两点,已知点A在点B的左侧,求点A和点B的坐标.18. 已知二次函数 .求证:不论 为何实数,此二次函数的图象与 轴都有两个不同交点.19. 由数形结合思想知:解方程可以看成是求两个函数交点的横坐标。例如:解方程2x+3=-x-6可看成是求直线y=2x+3和直线y=-x-6的交点横坐标。利用这一思想方法,借助函数图象,判断方程: 的实数根有几个。20. 抛物线y=x2+2x+m与x轴有两个不同的交点,求m的取值范围.