（人教版）2022-2023学年度第一学期九年级数学22.1.3 二次函数y=a（x-h）2+k的图像和性质同步测试

试卷更新日期：2022-07-08 类型：同步测试

进入出卷网下载

一、单选题

1. 点P（x₁ ， y₁），Q（x₂ ， y₂）在抛物线y＝ax²-4ax＋2（a＞0）上，若对于t＜x₁＜t＋1，t＋2＜x₂＜t＋3，都有y₁≠y₂ ，则t的取值范围是（）

A、t≥1 B、t≤0 C、t≥1或t≤0 D、t≥1或t≤-1

查看试题解析
2. 已知抛物线 $y = 2 {(x - 3)}^{2} - 5$ ，其对称轴是（）

A、直线 $x = - 3$ B、直线 $x = 3$ C、直线 $x = - 5$ D、直线 $x = 5$

查看试题解析
3. 抛物线 $y = - 2 {(x - 1)}^{2} + 2$ 的对称轴是直线（）

A、 $x = - 1$ B、 $x = 1$ C、 $x = - 2$ D、 $x = 2$

查看试题解析
4. 二次函数 $y = 2 {(x - 3)}^{2}$ 的顶点坐标为（）．

A、 $(3 ， 0)$ B、 $(- 3 ， 0)$ C、 $(0 ， - 3)$ D、 $(0 ， 3)$

查看试题解析
5. 下列关于二次函数 $y = - (x - m)^{2} + m^{2} - 2$ （m为常数）的结论：①该函数的图象与函数 $y = - x^{2}$ 的图象形状相同；②该函数的图象一定经过点 $(0 ， - 2)$ ；③当 $x < 0$ 时，y随x的增大而增大；④该函数的图象与函数 $y = 2 x^{2} - 4 m x - 1$ 的图象的对称轴相同．其中所有正确结论的序号是（）

A、①② B、①②④ C、①③④ D、②④

查看试题解析
6. 下列二次函数的图象中，顶点在第二象限的是（）

A、 $y = {(x - 1)}^{2} + 3$ B、 $y = {(x - 1)}^{2} - 3$ C、 $y = {(x + 1)}^{2} + 3$ D、 $y = {(x + 1)}^{2} - 3$

查看试题解析
7. 二次函数 $y = {(x - 1)}^{2} - 3$ 的最小值是（）

A、－3 B、3 C、0 D、 $1$

查看试题解析
8. 关于二次函数y=-（x -2）²＋3，以下说法正确的是（）

A、当x＞-2时，y随x增大而减小 B、当x＞-2时，y随x增大而增大 C、当x＞2时，y随x增大而减小 D、当x＞2时，y随x增大而增大

查看试题解析
9. 对于二次函数 $y = - 4 (x + 6)^{2} - 5$ 的图象，下列说法正确的是（）

A、图象与y轴交点的坐标是 $(0 ， - 5)$ B、对称轴是直线 $x = 6$ C、顶点坐标为 $(- 6 ， 5)$ D、当 $x < - 6$ 时，y随x的增大而增大

查看试题解析
10. 对于二次函数 $y = - (x - 1)^{2}$ 的图象，下列说法错误的是（）

A、开口向下 B、对称轴是直线 $x = 1$ C、顶点坐标为（1，0） D、当 $x < 1$ 时，y随x的增大而减小

查看试题解析

二、填空题

11. 抛物线 $y = - \frac{1}{2} {(x - 2)}^{2} + 5$ 的顶点坐标是.

查看试题解析
12. 二次函数y＝（x﹣1）² ，当x＜1时，y随x的增大而（填“增大”或“减小”）．

查看试题解析
13. 已知点 $A (x_{1} ， y_{1})$ 、 $B (x_{2} ， y_{2})$ 为函数 $y = - 2 {(x - 1)}^{2} + 3$ 的图象上的两点，若 $x_{1} < x_{2} < 0$ ，则 $y_{1}$ $y_{2}$ （填“>”、“=”或“<”）．

查看试题解析
14. 如果抛物线 $y = {(x - 2)}^{2} + k$ 不经过第三象限，那么k的值可以是．（只需写一个）

查看试题解析
15. 已知二次函数y＝3（x﹣5）² ，当x分别取x₁ ， x₂（x₁≠x₂）时，函数值相等，则当x＝ $\frac{x_{1} + x_{2}}{2}$ 时，函数值为．

查看试题解析

三、解答题

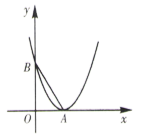
16. 已知二次函数 $y = 2 {(x - 1)}^{2}$ 的图象如图所示，求 $△ A B O$ 的面积.

查看试题解析
17. 当﹣2≤x≤1时，二次函数y＝﹣（x﹣m）²+m²+1有最大值4，求实数m的值.

查看试题解析
18. 已知关于x的方程x²﹣2mx+3+4m²﹣6=0的两根为α，β，
试求（α﹣1）²+（β﹣1）²的最大值与最小值．

查看试题解析
19. 画出函数的图象，写出它的开口方向，对称轴和顶点，并说明当y随x的增大而增大时，x的取值范围．

查看试题解析
20. 已知关于x的一元二次方程x²+2x+k﹣1=0有实数根，k为正整数．
（1）求k的值；
（2）当此方程有两个非零的整数根时，求关于x的二次函数y=x²+2x+k﹣1的图象的对称轴和顶点坐标．

查看试题解析
21. 求二次函数y=﹣2（x﹣3）²﹣5的顶点坐标．

查看试题解析
22. 在同一坐标系内，画出函数y=2x²和y=2（x-1）²+1的图象，并说出它们的相同点和不同点．

查看试题解析
23. 用配方法把二次函数 $y = - 2 x^{2} + 6 x + 4$ 化为 $y = a {(x + m)}^{2} + k$ 的形式，再指出该函数图象的开口方向、对称轴和顶点坐标.

查看试题解析

（人教版）2022-2023学年度第一学期九年级数学22.1.3 二次函数y=a（x-h）2+k的图像和性质 同步测试

一、单选题

二、填空题

三、解答题

（人教版）2022-2023学年度第一学期九年级数学22.1.3 二次函数y=a（x-h）2+k的图像和性质同步测试