（人教版）2022-2023学年度第一学期九年级数学22.1.1 二次函数同步测试

试卷更新日期：2022-07-08 类型：同步测试

进入出卷网下载

一、单选题

1. 下列函数表达式中，一定为二次函数的是（）

A、 $y = 5 x - 1$ B、 $y = a x^{2} + b x + c$ C、 $y = 3 x^{2} + 1$ D、 $y = x^{2} + \frac{1}{x}$

查看试题解析
2. 正方形的面积y与它的周长x满足的函数关系是（）

A、正比例函数 B、一次函数 C、二次函数 D、反比例函数

查看试题解析
3. 在下列关于x的函数中，一定是二次函数的是（）

A、 $y = - 3 x$ B、 $x y = 2$ C、 $y = a x^{2} + b x + c$ D、 $y = 2 x^{2} + 5$

查看试题解析
4. 若函数 $y = (3 - 2 m) x^{m^{2} - 7} - x + 1$ 是二次函数，则m的值为（）

A、3 B、-3 C、 $\pm 3$ D、9

查看试题解析
5. 若函数 $y = (1 + m) x^{m^{2} - 2 m - 1}$ 是关于x的二次函数，则m的值是（）

A、2 B、-1或3 C、3 D、-1± $\sqrt{2}$

查看试题解析
6. 若y=(a+1)x^la+3l-x+3是关于x的二次函数，则a的值是（）

A、1 B、-5 C、-1 D、-5或-1

查看试题解析
7. 已知 $y = (m + 1) x^{| m - 1 |} + 2 m$ 是y关于x的二次函数，则m的值为（）

A、 $- 1$ B、 $3$ C、 $- 1$ 或 $3$ D、 $0$

查看试题解析
8. 若 $y = (m - 2) x^{2} - x + 1$ 是二次函数，则（）

A、 $m \neq 0$ B、 $m > 2$ C、 $m < 2$ D、 $m \neq 2$

查看试题解析
9. 已知y=(m+ 1)x^|m-1|+2m是y关于x的二次函数，则m的值为（）

A、-1 B、3 C、-1或3 D、0

查看试题解析
10. 某商品的进价为每件20元，现在的售价为每件40元，每星期可卖出200件．市场调查反映：如调整价格，每涨价1元，每星期要少卖出5件．则每星期售出商品的利润y（单位：元）与每件涨价x（单位：元）之间的函数关系式是（）

A、y＝（200﹣5x）（40﹣20＋x） B、y＝（200＋5x）（40﹣20﹣x） C、y＝200（40﹣20﹣x） D、y＝200﹣5x

查看试题解析

二、填空题

11. 若 $y = (m^{2} + m) x^{m^{2} + 1} - x + 3$ 是关于x的二次函数，则m= ．

查看试题解析
12. 若关于x的函数y＝（1﹣a）x²﹣x是二次函数，则a的取值范围是

查看试题解析
13. 已知函数 $y = (m - 1) x^{m^{2} + 1} + 5 x - 3$ 的图象是抛物线，则m=.

查看试题解析
14. 已知y＝（k－2）x^|k|＋2x－3是二次函数，则实数k＝

查看试题解析
15. 如果函数 $y = (k - 3) x^{k^{2} - 3 k + 2} + k x + 1$ 是二次函数，那么k的值一定是．

查看试题解析

三、解答题

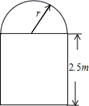
16. 当m为何值时，函数 $y = (m + 1) x^{m^{2} - 2 m - 1} + 8 x - 1$ 是二次函数．

查看试题解析
17. 一条隧道的横截面如图所示，它的上部是一个半圆，下部是一个矩形，矩形的一边长为 $2.5$ 米．如果隧道下部的宽度大于 $5$ 米但不超过 $10$ 米，求隧道横截面积 $S$ （平方米）关于上部半圆半径 $r$ （米）的函数解析式及函数的定义域．

查看试题解析
18. 已知y=(m-2) $x^{m^{2} -m}$ +3x+6是二次函数，求m的值，并判断此抛物线的开口方向，写出对称轴及顶点坐标.

查看试题解析
19. 如图，在四边形ABCD中，∠BAD＝∠ACB＝90°，AB＝AD，AC＝4BC，设CD的长为x，四边形ABCD的面积为y，求y与x之间的函数表达式．

查看试题解析
20. 已知函数y=（9k²﹣1）x²+2kx+3是关于x的二次函数，求不等式 $\frac{k - 1}{2} \geq \frac{4 k + 1}{3} - 1$ 的解集．

查看试题解析
21. 已知y=（m﹣1）x $^{m^{2} + 2 m - 1}$ 是关于x的二次函数，求m的值．

查看试题解析
22. 某种产品的年产量不超过1 000t，该产品的年产量（t）与费用（万元）之间的函数关系如图（1）；该产品的年销售量（t）与每吨销售价（万元）之间的函数关系如图（2）．若生产出的产品都能在当年销售完，则年产量为多少吨时，当年可获得7500万元毛利润？（毛利润=销售额﹣费用）

查看试题解析
23. 已知关于x的一元二次方程x²+2x+ $\frac{k - 1}{2}$ =0有实数根，k为正整数．
（1）求k的值；
（2）当此方程有两个非零的整数根时，将关于x的二次函数y=x²+2x+ $\frac{k - 1}{2}$ 的图象向下平移9个单位，求平移后的图象的表达式；
（3）在（2）的条件下，平移后的二次函数的图象与x轴交于点A，B（点A在点B左侧），直线y=kx+b（k＞0）过点B，且与抛物线的另一个交点为C，直线BC上方的抛物线与线段BC组成新的图象，当此新图象的最小值大于﹣5时，求k的取值范围．

查看试题解析

（人教版）2022-2023学年度第一学期九年级数学22.1.1 二次函数 同步测试

一、单选题

二、填空题

三、解答题

（人教版）2022-2023学年度第一学期九年级数学22.1.1 二次函数同步测试