2022年高考数学真题分类汇编专题12：统计与概率

试卷更新日期：2022-07-08 类型：二轮复习

进入出卷网下载

一、单选题

1. 有甲乙丙丁戊5名同学站成一排参加文艺汇演，若甲不站在两端，丙和丁相邻的不同排列方式有多少种（）

A、12种 B、24种 C、36种 D、48种

查看试题解析
2. 分别统计了甲、乙两位同学16周的各周课外体育运动时长（单位：h），得如下茎叶图：

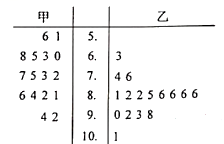
则下列结论中错误的是（）

A、甲同学周课外体育运动时长的样本中位数为7.4 B、乙同学周课外体育运动时长的样本平均数大于8 C、甲同学周课外体育运动时长大于8的概率的估计值大于0.4 D、乙同学周课外体育运动时长大于8的概率的估计值大于0.6

查看试题解析
3. 某社区通过公益讲座以普及社区居民的垃圾分类知识．为了解讲座效果，随机抽取10位社区居民，让他们在讲座前和讲座后各回答一份垃圾分类知识问卷，这10位社区居民在讲座前和讲座后问卷答题的正确率如下图：

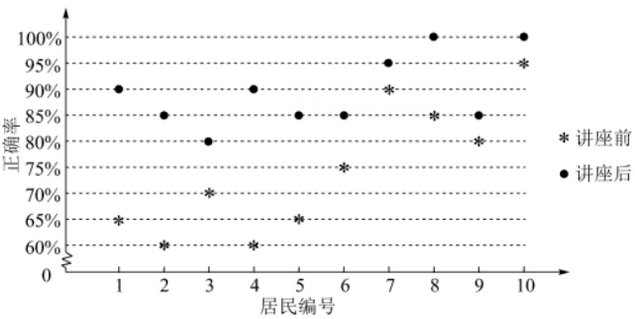
则（）

A、讲座前问卷答题的正确率的中位数小于70% B、讲座后问卷答题的正确率的平均数大于85% C、讲座前问卷答题的正确率的标准差小于讲座后正确率的标准差 D、讲座后问卷答题的正确率的极差大于讲座前正确率的极差

查看试题解析
4. 从分别写有1，2，3，4，5，6的6张卡片中无放回随机抽取2张，则抽到的2张卡片上的数字之积是4的倍数的概率为（）

A、 $\frac{1}{5}$ B、 $\frac{1}{3}$ C、 $\frac{2}{5}$ D、 $\frac{2}{3}$

查看试题解析
5. 某棋手与甲、乙、丙三位棋手各比赛一盘，各盘比赛结果相互独立．已知该棋手与甲、乙、丙比赛获胜的概率分别为 $p_{1} ， p_{2} ， p_{3}$ ，且 $p_{3} > p_{2} > p_{1} > 0$ ．记该棋手连胜两盘的概率为p，则（）

A、p与该棋手和甲、乙、丙的此赛次序无关 B、该棋手在第二盘与甲比赛，p最大 C、该棋手在第二盘与乙比赛，p最大 D、该棋手在第二盘与丙比赛，p最大

查看试题解析
6. 若 ${(2 x - 1)}^{4} = a_{4} x^{4} + a_{3} x^{3} + a_{2} x^{2} + a_{1} x + a_{0}$ ，则 $a_{0} + a_{2} + a_{4} =$ （）

A、40 B、41 C、-40 D、-41

查看试题解析
7. 从2至8的7个整数中随机取2个不同的数，则这2个数互质的概率为（）

A、 $\frac{1}{6}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析

二、填空题

8. 现有7张卡片，分别写上数字1，2，2，3，4，5，6．从这7张卡片中随机抽取3张，记所抽取卡片上数字的最小值为 $ξ$ ，则 $P (ξ = 2) =$ ， $E (ξ) =$ ．

查看试题解析
9. 已知多项式 $(x + 2) {(x - 1)}^{4} = a_{0} + a_{1} x + a_{2} x^{2} + a_{3} x^{3} + a_{4} x^{4} + a_{5} x^{5}$ ，则 $a_{2} =$ ， $a_{1} + a_{2} + a_{3} + a_{4} + a_{5} =$ ．

查看试题解析
10. 已知随机变量X服从正态分布 $N (2 ， σ^{2})$ ，且 $P (2 < X \leq 2.5) = 0.36$ ，则 $P (X > 2.5) =$ ．

查看试题解析
11. 从正方体的8个顶点中任选4个，则这4个点在同一个平面的概率为．

查看试题解析
12. 从甲、乙等5名同学中随机选3名参加社区服务工作，则甲、乙都入选的概率为．

查看试题解析
13. $(1 - \frac{y}{x}) {(x + y)}^{8}$ 的展开式中 $x^{2} y^{6}$ 的系数为 (用数字作答).

查看试题解析
14. 在 ${(x^{3} + \frac{1}{x})}^{12}$ 的展开式中，含 $\frac{1}{x^{4}}$ 项的系数为

查看试题解析
15. 已知有1、2、3、4四个数字组成无重复数字，则比2134大的四位数的个数为

查看试题解析

三、解答题

16. 在某地区进行流行病调查，随机调查了100名某种疾病患者的年龄，得到如下的样本数据频率分布直方图．

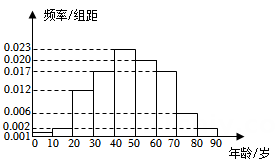(1)、估计该地区这种疾病患者的平均年龄（同一组中的数据用该组区间的中点值作代表）；

(2)、估计该地区一人患这种疾病年龄在区间 $[20 ， 70)$ 的概率；

(3)、已知该地区这种疾病的患病率为0.1%，该地区年龄位于区间 $[40 ， 50)$ 的人口占该地区总人口的16%，从该地区任选一人，若此人年龄位于区间 $[40 ， 50)$ ，求此人患该种疾病的概率．（样本数据中的患者年龄位于各区间的频率作为患者年龄位于该区间的概率，精确到0.0001）

查看试题解析
17. 甲、乙两个学校进行体育比赛，比赛共设三个项目，每个项目胜方得10分，负方得0分，没有平局．三个项目比赛结束后，总得分高的学校获得冠军．已知甲学校在三个项目中获胜的概率分别为0.5，0.4，0.8，各项目的比赛结果相互独立．

(1)、求甲学校获得冠军的概率；

(2)、用X表示乙学校的总得分，求X的分布列与期望．

查看试题解析
18. 甲、乙两城之间的长途客车均由A和B两家公司运营，为了解这两家公司长途客车的运行情况，随机调查了甲、乙两城之间的500个班次，得到下面列联表：

准点班次数

未准点班次数

A

240

20

B

210

30

附： $K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，

$P (K^{2} ⩾ k)$

0.100

0.050

0.010

$k$

2.706

3.841

6.635

(1)、根据上表，分别估计这两家公司甲、乙两城之间的长途客车准点的概率；

(2)、能否有90%的把握认为甲、乙两城之间的长途客车是否准点与客车所属公司有关？

查看试题解析

19. 某地经过多年的环境治理，已将荒山改造成了绿水青山．为估计一林区某种树木的总材积量，随机选取了10棵这种树木，测量每棵树的根部横截面积（单位：

m^{2}

）和材积量（单位：

m^{3}

），得到如下数据：

样本号i	1	2	3	4	5	6	7	8	9	10	总和
根部横截面积 $x_{i}$	0.04	0.06	0.04	0.08	0.08	0.05	0.05	0.07	0.07	0.06	0.6
材积量 $y_{i}$	0.25	0.40	0.22	0.54	0.51	0.34	0.36	0.46	0.42	0.40	3.9

并计算得 $\sum_{i=1}^{10} x_{i}^{2} = 0.038 ， \sum_{i=1}^{10} y_{i}^{2} = 1.6158 ， \sum_{i=1}^{10} x_{i} y_{i} = 0.2474$ ．

附：相关系数 $r = \frac{\sum_{i =1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sqrt{\sum_{i =1}^{n} {(x_{i} - \bar{x})}^{2} \sum_{i =1}^{n} {(y_{i} - \bar{y})}^{2}}} ， \sqrt{1.896} \approx 1.377$ ．

(1)、估计该林区这种树木平均一棵的根部横截面积与平均一棵的材积量；

(2)、求该林区这种树木的根部横截面积与材积量的样本相关系数（精确到0.01）；

(3)、现测量了该林区所有这种树木的根部横截面积，并得到所有这种树木的根部横截面积总和为

{186m}^{2}

．已知树木的材积量与其根部横截面积近似成正比．利用以上数据给出该林区这种树木的总材积量的估计值．

查看试题解析

20. 在校运动会上，只有甲、乙、丙三名同学参加铅球比赛，比赛成绩达到9.50m以上（含9.50m）的同学将获得优秀奖，为预测获得优秀奖的人数及冠军得主，收集了甲、乙、丙以往的比赛成绩，并整理得到如下数据（单位：m）：
甲：9.80， 9.70， 9.55， 9.54， 9.48， 9.42， 9.40， 9.35， 9.30， 9.25；

乙：9.78， 9.56， 9.51， 9.36， 9.32， 9.23；

丙：9.85， 9.65， 9.20， 9.16．

假设用频率估计概率，且甲、乙、丙的比赛成绩相互独立

（I）估计甲在校运动会铅球比赛中获得优秀奖的概率；

（II）设X是甲、乙、丙在校运动会铅球比赛中获得优秀奖的总人数，估计 $X$ 的数学期望 $E X$ ；

（III）在校运动会铅球比赛中，甲、乙、丙谁获得冠军的概率估计值最大？（结论不要求证明）

查看试题解析
21. 一医疗团队为研究某地的一种地方性疾病与当地居民的卫生习惯(卫生习惯分为良好和不够良好两类)的关系，在己患该疾病的病例中随机调查了100例(称为病例组)，同时在未患该疾病的人群中随机调查了100人(称为对照组)，得到如下数据：

不够良好良好

病例组 40 60

对照组 10 90

附： $K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$

P(K² ≥ k)

0.050

0.010

0.001

K

3.841

6.635

10.828

(1)、能否有99%的把握认为患该疾病群体与未患该疾病群体的卫生习惯有差异?

(2)、从该地的人群中任选一人，A表示事件“选到的人卫生习惯不够良好”，B表示事件“选到的人患有该疾病”， $\frac{P (B ∣ A)}{P (\bar{B} ∣ A)}$ 与 $\frac{P (B ∣ \bar{A})}{P (\bar{B} ∣ \bar{A})}$ 的比值是卫生习惯不够良好对患该
疾病风险程度的一项度量指标，记该指标为R.

(i)证明： $R = \frac{P (A ∣ B)}{P (\bar{A} ∣ B)} \cdot \frac{P (\bar{A} ∣ \bar{B})}{P (A ∣ \bar{B})} ；$

(ii)利用该调查数据，给出 $P (A | B) ， P (A ∣ \bar{B})$ 的估计值，并利用(i)的结果给出R的估计值.

查看试题解析

	准点班次数	未准点班次数
A	240	20
B	210	30

$P (K^{2} ⩾ k)$	0.100	0.050	0.010
$k$	2.706	3.841	6.635

	不够良好	良好
病例组	40	60
对照组	10	90

P(K² ≥ k)	0.050	0.010	0.001
K	3.841	6.635	10.828