2022年高考数学真题分类汇编专题11:立体几何
试卷更新日期:2022-07-08 类型:二轮复习
一、单选题
-
1. 某几何体的三视图如图所示(单位: ),则该几何体的体积(单位: )是( )
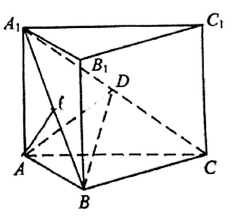
 A、 B、 C、 D、2. 如图,已知正三棱柱 ,E,F分别是棱 上的点.记 与 所成的角为 , 与平面 所成的角为 ,二面角 的平面角为 ,则( )
A、 B、 C、 D、2. 如图,已知正三棱柱 ,E,F分别是棱 上的点.记 与 所成的角为 , 与平面 所成的角为 ,二面角 的平面角为 ,则( ) A、 B、 C、 D、3. 正三棱台高为1,上下底边长分别为 和 ,所有顶点在同一球面上,则球的表面积是( )A、100π B、128π C、144π D、192π4. 如图,网格纸上绘制的是一个多面体的三视图,网格小正方形的边长为1,则该多面体的体积为( )
A、 B、 C、 D、3. 正三棱台高为1,上下底边长分别为 和 ,所有顶点在同一球面上,则球的表面积是( )A、100π B、128π C、144π D、192π4. 如图,网格纸上绘制的是一个多面体的三视图,网格小正方形的边长为1,则该多面体的体积为( )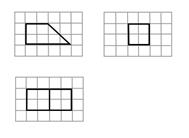 A、8 B、12 C、16 D、205. 甲、乙两个圆锥的母线长相等,侧面展开图的圆心角之和为 ,侧面积分别为 和 ,体积分别为 和 .若 ,则 ( )A、 B、 C、 D、6. 在长方体 中,已知 与平面 和平面 所成的角均为 ,则( )A、 B、AB与平面 所成的角为 C、 D、 与平面 所成的角为7. 在正方体 中,E,F分别为 的中点,则( )A、平面 平面 B、平面 平面 C、平面 平面 D、平面 平面8. 已知球O的半径为1,四棱锥的顶点为O,底面的四个顶点均在球O的球面上,则当该四棱锥的体积最大时,其高为( )A、 B、 C、 D、9. 已知正三棱锥 的六条棱长均为6, 是 及其内部的点构成的集合,设集合 ,则 表示的区域的面积为( )A、 B、 C、 D、10. 已知正四棱锥的侧棱长为 ,其各顶点都在同一球面上.若该球的体积为36 ,且 则该正四棱锥体积的取值范围是( )A、 B、 C、 D、[18,27]11. 南水北调工程缓解了北方一些地区水资源短缺问题,其中一部分水蓄入某水库。知该水库水位为海拔148.5m时,相应水面的面积为 水位为海拔157.5m时,相应水面的面积为 将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔148.5m上升到157.5m时,增加的水量约为( )A、 B、 C、 D、12. 某几何体的三视图如图所示,则这个几何体可能是()
A、8 B、12 C、16 D、205. 甲、乙两个圆锥的母线长相等,侧面展开图的圆心角之和为 ,侧面积分别为 和 ,体积分别为 和 .若 ,则 ( )A、 B、 C、 D、6. 在长方体 中,已知 与平面 和平面 所成的角均为 ,则( )A、 B、AB与平面 所成的角为 C、 D、 与平面 所成的角为7. 在正方体 中,E,F分别为 的中点,则( )A、平面 平面 B、平面 平面 C、平面 平面 D、平面 平面8. 已知球O的半径为1,四棱锥的顶点为O,底面的四个顶点均在球O的球面上,则当该四棱锥的体积最大时,其高为( )A、 B、 C、 D、9. 已知正三棱锥 的六条棱长均为6, 是 及其内部的点构成的集合,设集合 ,则 表示的区域的面积为( )A、 B、 C、 D、10. 已知正四棱锥的侧棱长为 ,其各顶点都在同一球面上.若该球的体积为36 ,且 则该正四棱锥体积的取值范围是( )A、 B、 C、 D、[18,27]11. 南水北调工程缓解了北方一些地区水资源短缺问题,其中一部分水蓄入某水库。知该水库水位为海拔148.5m时,相应水面的面积为 水位为海拔157.5m时,相应水面的面积为 将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔148.5m上升到157.5m时,增加的水量约为( )A、 B、 C、 D、12. 某几何体的三视图如图所示,则这个几何体可能是() A、棱柱 B、圆柱 C、圆台 D、球13. 如图,正方体 中,N是棱 的中点,则直线CN与平面 所成角的正弦值等于( )
A、棱柱 B、圆柱 C、圆台 D、球13. 如图,正方体 中,N是棱 的中点,则直线CN与平面 所成角的正弦值等于( )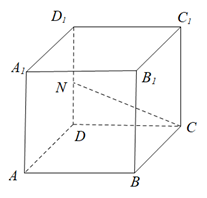 A、 B、 C、 D、14. 如图,上海海关大楼的上面可以看作一个正四棱柱,四个侧面有四个时钟,则相邻两个时钟的时针从0时转到12时(含0时不含12时)的过程中,能够相互垂直( )次
A、 B、 C、 D、14. 如图,上海海关大楼的上面可以看作一个正四棱柱,四个侧面有四个时钟,则相邻两个时钟的时针从0时转到12时(含0时不含12时)的过程中,能够相互垂直( )次 A、0 B、2 C、4 D、12
A、0 B、2 C、4 D、12二、多选题
-
15. 如图,四边形 为正方形, 平面 , ,记三棱锥 , , 的体积分别为 ,则( )
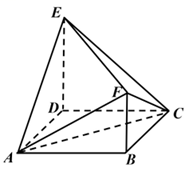 A、 B、 C、 D、16. 已知正方体 则( )A、直线 与 所成的角为 B、直线 与 所成的角为 C、直线 与平面 所成的角为 D、直线 与平面ABCD所成的角为
A、 B、 C、 D、16. 已知正方体 则( )A、直线 与 所成的角为 B、直线 与 所成的角为 C、直线 与平面 所成的角为 D、直线 与平面ABCD所成的角为三、填空题
-
17. 如图,E,F分别是三棱锥V-ABC两条棱AB,VC上的动点,且满足 则 的最小值为.

四、解答题
-
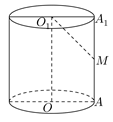
18. 如图,已知 和 都是直角梯形, , , , , , ,二面角 的平面角为 .设M,N分别为 的中点.
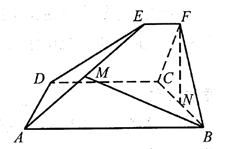
(Ⅰ)证明: ;
(Ⅱ)求直线 与平面 所成角的正弦值.
19. 如图, 是三棱锥 的高, , ,E是 的中点.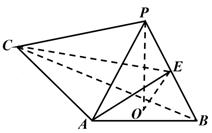 (1)、求证: 平面 ;(2)、若 , , ,求二面角 的正弦值.20. 如图,四面体 中, ,E为AC的中点.
(1)、求证: 平面 ;(2)、若 , , ,求二面角 的正弦值.20. 如图,四面体 中, ,E为AC的中点.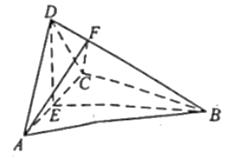 (1)、证明:平面 平面ACD;(2)、设 ,点F在BD上,当 的面积最小时,求三棱锥 的体积.21. 在四棱锥 中, 底面 .
(1)、证明:平面 平面ACD;(2)、设 ,点F在BD上,当 的面积最小时,求三棱锥 的体积.21. 在四棱锥 中, 底面 .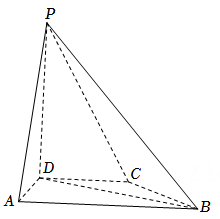 (1)、证明: ;(2)、求PD与平面 所成的角的正弦值.22. 小明同学参加综合实践活动,设计了一个封闭的包装盒,包装盒如图所示:底面 是边长为8(单位:cm)的正方形, 均为正三角形,且它们所在的平面都与平面 垂直.
(1)、证明: ;(2)、求PD与平面 所成的角的正弦值.22. 小明同学参加综合实践活动,设计了一个封闭的包装盒,包装盒如图所示:底面 是边长为8(单位:cm)的正方形, 均为正三角形,且它们所在的平面都与平面 垂直.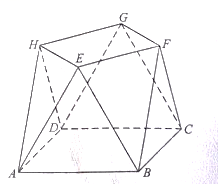 (1)、证明: 平面 ;(2)、求该包装盒的容积(不计包装盒材料的厚度).23. 如图,四面体 中, ,E为 的中点.
(1)、证明: 平面 ;(2)、求该包装盒的容积(不计包装盒材料的厚度).23. 如图,四面体 中, ,E为 的中点. (1)、证明:平面 平面 ;(2)、设 ,点F在 上,当 的面积最小时,求 与平面 所成的角的正弦值.24. 如图,在三棱柱 中,侧面 为正方形,平面 平面 , , 分别为 , 的中点.
(1)、证明:平面 平面 ;(2)、设 ,点F在 上,当 的面积最小时,求 与平面 所成的角的正弦值.24. 如图,在三棱柱 中,侧面 为正方形,平面 平面 , , 分别为 , 的中点.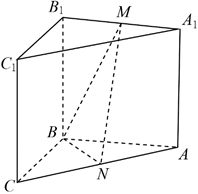
(I)求证: 平面 ;
(II)再从条件①、条件②这两个条件中选择一个作为已知,求
直线 与平面 所成角的正弦值。
条件①: ;
条件②: .
注:如果选择条件①和条件②分别解答,按第一个解答计分。
-