（人教版）2022-2023学年度第一学期九年级数学21.2.2 解一元二次方程---公式法同步测试

试卷更新日期：2022-07-08 类型：同步测试

进入出卷网下载

一、单选题

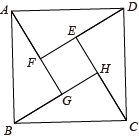
1. 一元二次方程 $x^{2} + x - 3 = 0$ 的根的情况是（）

A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根

查看试题解析
2. 下列方程有两个相等的实数根的是（）

A、x²﹣2x+1＝0 B、x²﹣3x+2＝0 C、x²﹣2x+3＝0 D、x²﹣9＝0

查看试题解析
3. 直线y= $x$ +a不经过第四象限，则关于 $x$ 的方程a $x^{2}$ -2 $x$ -1=0的实数解的个数是（）

A、0个 B、1个 C、2个 D、1个或2个

查看试题解析
4. 若一元二次方程x²＋mx＋4＝0有两个相等的实数根，则m的值是（）

A、2 B、±2 C、±4 D、±2 $\sqrt{2}$

查看试题解析
5. 已知关于x的方程 $x^{2} - 2 x - 1 = 0$ ，则下列关于该方程根的判断，正确的是（）

A、没有实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、不能确定

查看试题解析
6. 关于x的一元二次方程mx²+（2m﹣4）x+（m﹣2）＝0有两个实数根，则m的取值范围（）

A、m≥2 B、m≤2 C、m≥2且m≠0 D、m≤2且m≠0

查看试题解析
7. 下列方程中没有实数根的是（）

A、 $x^{2} - 2 x + 2 = 0$ B、 $x^{2} - 4 x + 4 = 0$ C、 $x (x - 2) = 0$ D、 ${(x - 1)}^{2} = 3$

查看试题解析
8. 2002年国际数学家大会在北京召开，大会的会标是我国古代数学家赵爽画的“弦图”（如图），体现了数学研究的继承和发展，弦图中四边形ABCD与EFGH均为正方形，若 $A G = B H = C E = D F = a ，$ $A F = B G = C H = D E = b ，$ 且正方形EFGH的面积为正方形ABCD的面积的一半，则a：b的值为（）

A、 $2 - \sqrt{3}$ B、 $\sqrt{2}$ C、2 D、 $2 + \sqrt{3}$

查看试题解析
9. 若关于x的一元二次方程ax²﹣4x＋2＝0有两个实数根，则a的取值范围是（）

A、a≤2 B、a≤2且a≠0 C、a＜2 D、a＜2且a≠0

查看试题解析
10. 关于x的一元二次方程 $x^{2} - 3 x + n = 0$ 没有实数根，则实数n的值可以为（）

A、0 B、1 C、2 D、3

查看试题解析

二、填空题

11. 若关于 $x$ 的一元二次方程 $x^{2} - 2 x + m = 0$ 有两个不相等的实数根，则实数 $m$ 的取值范围是.

查看试题解析
12. 若关于x的一元二次方程 $x^{2} + 2 x + a = 0$ 有两个不相等实数根，则实数a的取值范围是．

查看试题解析
13. 若一元二次方程x²-4x+k+2=0有两个不相等的实数根，则k的取值范围是.

查看试题解析
14. 已知关于x的方程x²＋2（m﹣1）x＋m²＝0有实数根，则m的最大整数值是．

查看试题解析
15. 若关于 x 的一元二次方程x²-2x+b=0有两个相等的实数根，则 b 的值为.

查看试题解析

三、解答题

16. 等腰三角形的三边长分别为 $a$ 、 $b$ 、 $c$ ，若 $a = 6$ ， $b$ 与 $c$ 是方程 $x^{2} - (3 m + 1) x + 2 m^{2} + 2 m = 0$ 的两根，求此三角形的周长．

查看试题解析
17. 关于x的方程x²﹣（k+1）x+k＝0有两个相等的实数根，求k的值．

查看试题解析
18. 已知关于x的方程x²+kx+k-2＝0，证明不论k为什么实数，这个方程总有两个不相等实数根．

查看试题解析
19. 如果关于 $x$ 的方程 $m x^{2} - 2 (m + 2) x + m + 5 = 0$ 没有实数根，试判断关于 $x$ 的方程 $(m - 5) x^{2} - 2 (m - 1) x + m = 0$ 的根的情况.

查看试题解析
20. 已知：关于x的一元二次方程x²+kx﹣1=0，求证：方程有两个不相等的实数根．

查看试题解析
21. 已知关于 $x$ 的一元二次方程 $x^{2} - 3 x + m - 2 = 0$ 有两实数根 $x_{1} ， x_{2}$ ，求 $m$ 的取值范围

查看试题解析
22. 已知：关于x的一元二次方程（k﹣1）x²+2x﹣1＝0有两个不相等的实数根．求：k的最小整数解．

查看试题解析
23. 关于 $x$ 的方程 $x^{2} - 2 x + 2 m - 1 = 0$ 有实数根，且 $m$ 为正整数，求 $m$ 的值．

查看试题解析

（人教版）2022-2023学年度第一学期九年级数学21.2.2 解一元二次方程---公式法 同步测试

一、单选题

二、填空题

三、解答题

（人教版）2022-2023学年度第一学期九年级数学21.2.2 解一元二次方程---公式法同步测试