2020--2022年三年全国高考物理真题汇编:动量
试卷更新日期:2022-07-08 类型:二轮复习
一、单选题
-
1. 一质点做曲线运动,在前一段时间内速度大小由v增大到2v,在随后的一段时间内速度大小由2v增大到5v。前后两段时间内,合外力对质点做功分别为W1和W2 , 合外力的冲量大小分别为I1和I2。下列关系式一定成立的是( )A、W2=3W1 , I2≤3I1 , B、W2=3W1 , I2≥I1 C、W2=7W1 , I2≤3I1 , D、W2=7W1 , I2≥I12. 风力发电已成为我国实现“双碳”目标的重要途经之一。如图所示,风力发电机是一种将风能转化为电能的装置。某风力发电机在风速为9m/s时,输出电功率为405kW,风速在5~10m/s范围内,转化效率可视为不变。该风机叶片旋转一周扫过的面积为A,空气密度为ρ,风场风速为v,并保持风正面吹向叶片。下列说法正确的是( )
 A、该风力发电机的输出电功率与风速成正比 B、单位时间流过面积A的流动空气动能为 C、若每天平均有1.0×108kW的风能资源,则每天发电量为2.4×109kW·h D、若风场每年有5000h风速在6~10m/s的风能资源,则该发电机年发电量至少为6.0×105kW·h3. 1932年,查德威克用未知射线轰击氢核,发现这种射线是由质量与质子大致相等的中性粒子(即中子)组成。如图,中子以速度 分别碰撞静止的氢核和氮核,碰撞后氢核和氮核的速度分别为 和 。设碰撞为弹性正碰,不考虑相对论效应,下列说法正确的是( )
A、该风力发电机的输出电功率与风速成正比 B、单位时间流过面积A的流动空气动能为 C、若每天平均有1.0×108kW的风能资源,则每天发电量为2.4×109kW·h D、若风场每年有5000h风速在6~10m/s的风能资源,则该发电机年发电量至少为6.0×105kW·h3. 1932年,查德威克用未知射线轰击氢核,发现这种射线是由质量与质子大致相等的中性粒子(即中子)组成。如图,中子以速度 分别碰撞静止的氢核和氮核,碰撞后氢核和氮核的速度分别为 和 。设碰撞为弹性正碰,不考虑相对论效应,下列说法正确的是( )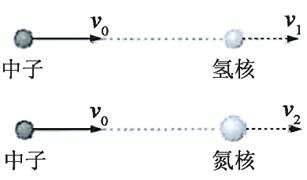 A、碰撞后氮核的动量比氢核的小 B、碰撞后氮核的动能比氢核的小 C、 大于 D、 大于4. 抗日战争时期,我军缴获不少敌军武器武装自己,其中某轻机枪子弹弹头质量约8 g,出膛速度大小约750 m/s。某战士在使用该机枪连续射击1分钟的过程中,机枪所受子弹的平均反冲力大小约12 N,则机枪在这1分钟内射出子弹的数量约为( )A、40 B、80 C、120 D、1605. 物体的运动状态可用位置 和动量 描述,称为相,对应 图像中的一个点。物体运动状态的变化可用 图像中的一条曲线来描述,称为相轨迹。假如一质点沿 轴正方向做初速度为零的匀加速直线运动,则对应的相轨迹可能是( )A、
A、碰撞后氮核的动量比氢核的小 B、碰撞后氮核的动能比氢核的小 C、 大于 D、 大于4. 抗日战争时期,我军缴获不少敌军武器武装自己,其中某轻机枪子弹弹头质量约8 g,出膛速度大小约750 m/s。某战士在使用该机枪连续射击1分钟的过程中,机枪所受子弹的平均反冲力大小约12 N,则机枪在这1分钟内射出子弹的数量约为( )A、40 B、80 C、120 D、1605. 物体的运动状态可用位置 和动量 描述,称为相,对应 图像中的一个点。物体运动状态的变化可用 图像中的一条曲线来描述,称为相轨迹。假如一质点沿 轴正方向做初速度为零的匀加速直线运动,则对应的相轨迹可能是( )A、 B、
B、 C、
C、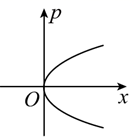 D、
D、 6. 如图,光滑水平地面上有一小车,一轻弹簧的一端与车厢的挡板相连,另一端与滑块相连,滑块与车厢的水平底板间有摩擦。用力向右推动车厢使弹簧压缩,撤去推力时滑块在车厢底板上有相对滑动。在地面参考系(可视为惯性系)中,从撤去推力开始,小车、弹簧和滑块组成的系统( )
6. 如图,光滑水平地面上有一小车,一轻弹簧的一端与车厢的挡板相连,另一端与滑块相连,滑块与车厢的水平底板间有摩擦。用力向右推动车厢使弹簧压缩,撤去推力时滑块在车厢底板上有相对滑动。在地面参考系(可视为惯性系)中,从撤去推力开始,小车、弹簧和滑块组成的系统( )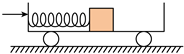 A、动量守恒,机械能守恒 B、动量守恒,机械能不守恒 C、动量不守恒,机械能守恒 D、动量不守恒,机械能不守恒7. 已知普朗克常量 ,电子的质量为 ,一个电子和一滴直径约为 的油滴具有相同动能,则电子与油滴的德布罗意波长之比的数量级为( )A、 B、 C、 D、8. 行驶中的汽车如果发生剧烈碰撞,车内的安全气囊会被弹出并瞬间充满气体。若碰撞后汽车的速度在很短时间内减小为零,关于安全气囊在此过程中的作用,下列说法正确的是( )A、增加了司机单位面积的受力大小 B、减少了碰撞前后司机动量的变化量 C、将司机的动能全部转换成汽车的动能 D、延长了司机的受力时间并增大了司机的受力面积9. 在同一竖直平面内,3个完全相同的小钢球(1号、2号、3号)悬挂于同一高度;静止时小球恰能接触且悬线平行,如图所示。在下列实验中,悬线始终保持绷紧状态,碰撞均为对心正碰。以下分析正确的是( )
A、动量守恒,机械能守恒 B、动量守恒,机械能不守恒 C、动量不守恒,机械能守恒 D、动量不守恒,机械能不守恒7. 已知普朗克常量 ,电子的质量为 ,一个电子和一滴直径约为 的油滴具有相同动能,则电子与油滴的德布罗意波长之比的数量级为( )A、 B、 C、 D、8. 行驶中的汽车如果发生剧烈碰撞,车内的安全气囊会被弹出并瞬间充满气体。若碰撞后汽车的速度在很短时间内减小为零,关于安全气囊在此过程中的作用,下列说法正确的是( )A、增加了司机单位面积的受力大小 B、减少了碰撞前后司机动量的变化量 C、将司机的动能全部转换成汽车的动能 D、延长了司机的受力时间并增大了司机的受力面积9. 在同一竖直平面内,3个完全相同的小钢球(1号、2号、3号)悬挂于同一高度;静止时小球恰能接触且悬线平行,如图所示。在下列实验中,悬线始终保持绷紧状态,碰撞均为对心正碰。以下分析正确的是( ) A、将1号移至高度 释放,碰撞后,观察到2号静止、3号摆至高度 。若2号换成质量不同的小钢球,重复上述实验,3号仍能摆至高度 B、将1、2号一起移至高度 释放,碰撞后,观察到1号静止,2、3号一起摆至高度 ,释放后整个过程机械能和动量都守恒 C、将右侧涂胶的1号移至高度 释放,1、2号碰撞后粘在一起,根据机械能守恒,3号仍能摆至高度 D、将1号和右侧涂胶的2号一起移至高度 释放,碰撞后,2、3号粘在一起向右运动,未能摆至高度 ,释放后整个过程机械能和动量都不守恒
A、将1号移至高度 释放,碰撞后,观察到2号静止、3号摆至高度 。若2号换成质量不同的小钢球,重复上述实验,3号仍能摆至高度 B、将1、2号一起移至高度 释放,碰撞后,观察到1号静止,2、3号一起摆至高度 ,释放后整个过程机械能和动量都守恒 C、将右侧涂胶的1号移至高度 释放,1、2号碰撞后粘在一起,根据机械能守恒,3号仍能摆至高度 D、将1号和右侧涂胶的2号一起移至高度 释放,碰撞后,2、3号粘在一起向右运动,未能摆至高度 ,释放后整个过程机械能和动量都不守恒二、多选题
-
10. 球形飞行器安装了可提供任意方向推力的矢量发动机,总质量为 。飞行器飞行时受到的空气阻力大小与其速率平方成正比(即 , 为常量)。当发动机关闭时,飞行器竖直下落,经过一段时间后,其匀速下落的速率为 ;当发动机以最大推力推动飞行器竖直向上运动,经过一段时间后,飞行器匀速向上的速率为 。重力加速度大小为 ,不考虑空气相对于地面的流动及飞行器质量的变化,下列说法正确的是( )A、发动机的最大推力为 B、当飞行器以 匀速水平飞行时,发动机推力的大小为 C、发动机以最大推力推动飞行器匀速水平飞行时,飞行器速率为 D、当飞行器以 的速率飞行时,其加速度大小可以达到11. 质量为 的物块在水平力F的作用下由静止开始在水平地面上做直线运动,F与时间t的关系如图所示。已知物块与地面间的动摩擦因数为0.2,重力加速度大小取 。则( )
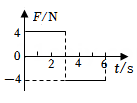 A、 时物块的动能为零 B、 时物块回到初始位置 C、 时物块的动量为 D、 时间内F对物块所做的功为12. 如图(a),质量分别为mA、mB的A、B两物体用轻弹簧连接构成一个系统,外力 作用在A上,系统静止在光滑水平面上(B靠墙面),此时弹簧形变量为 。撤去外力并开始计时,A、B两物体运动的 图像如图(b)所示, 表示0到 时间内 的 图线与坐标轴所围面积大小, 、 分别表示 到 时间内A、B的 图线与坐标轴所围面积大小。A在 时刻的速度为 。下列说法正确的是( )
A、 时物块的动能为零 B、 时物块回到初始位置 C、 时物块的动量为 D、 时间内F对物块所做的功为12. 如图(a),质量分别为mA、mB的A、B两物体用轻弹簧连接构成一个系统,外力 作用在A上,系统静止在光滑水平面上(B靠墙面),此时弹簧形变量为 。撤去外力并开始计时,A、B两物体运动的 图像如图(b)所示, 表示0到 时间内 的 图线与坐标轴所围面积大小, 、 分别表示 到 时间内A、B的 图线与坐标轴所围面积大小。A在 时刻的速度为 。下列说法正确的是( ) A、0到 时间内,墙对B的冲量等于mAv0 B、mA > mB C、B运动后,弹簧的最大形变量等于 D、13. 水平桌面上,一质量为m的物体在水平恒力F拉动下从静止开始运动,物体通过的路程等于 时,速度的大小为 ,此时撤去F,物体继续滑行 的路程后停止运动,重力加速度大小为g,则( )A、在此过程中F所做的功为 B、在此过中F的冲量大小等于 C、物体与桌面间的动摩擦因数等于 D、F的大小等于物体所受滑动摩擦力大小的2倍14. 如图所示,载有物资的热气球静止于距水平地面H的高处,现将质量为m的物资以相对地面的速度 水平投出,落地时物资与热气球的距离为d。已知投出物资后热气球的总质量为M , 所受浮力不变,重力加速度为g , 不计阻力,以下判断正确的是( )
A、0到 时间内,墙对B的冲量等于mAv0 B、mA > mB C、B运动后,弹簧的最大形变量等于 D、13. 水平桌面上,一质量为m的物体在水平恒力F拉动下从静止开始运动,物体通过的路程等于 时,速度的大小为 ,此时撤去F,物体继续滑行 的路程后停止运动,重力加速度大小为g,则( )A、在此过程中F所做的功为 B、在此过中F的冲量大小等于 C、物体与桌面间的动摩擦因数等于 D、F的大小等于物体所受滑动摩擦力大小的2倍14. 如图所示,载有物资的热气球静止于距水平地面H的高处,现将质量为m的物资以相对地面的速度 水平投出,落地时物资与热气球的距离为d。已知投出物资后热气球的总质量为M , 所受浮力不变,重力加速度为g , 不计阻力,以下判断正确的是( ) A、投出物资后热气球做匀加速直线运动 B、投出物资后热气球所受合力大小为 C、 D、15. 水平冰面上有一固定的竖直挡板,一滑冰运动员面对挡板静止在冰面上,他把一质量为4.0 kg的静止物块以大小为5.0 m/s的速度沿与挡板垂直的方向推向挡板,运动员获得退行速度;物块与挡板弹性碰撞,速度反向,追上运动员时,运动员又把物块推向挡板,使其再一次以大小为5.0 m/s的速度与挡板弹性碰撞。总共经过8次这样推物块后,运动员退行速度的大小大于5.0 m/s,反弹的物块不能再追上运动员。不计冰面的摩擦力,该运动员的质量可能为( )A、48 kg B、53 kg C、58 kg D、63 kg
A、投出物资后热气球做匀加速直线运动 B、投出物资后热气球所受合力大小为 C、 D、15. 水平冰面上有一固定的竖直挡板,一滑冰运动员面对挡板静止在冰面上,他把一质量为4.0 kg的静止物块以大小为5.0 m/s的速度沿与挡板垂直的方向推向挡板,运动员获得退行速度;物块与挡板弹性碰撞,速度反向,追上运动员时,运动员又把物块推向挡板,使其再一次以大小为5.0 m/s的速度与挡板弹性碰撞。总共经过8次这样推物块后,运动员退行速度的大小大于5.0 m/s,反弹的物块不能再追上运动员。不计冰面的摩擦力,该运动员的质量可能为( )A、48 kg B、53 kg C、58 kg D、63 kg三、综合题
-
16. 如图,光滑水平面上有两个等高的滑板A和B,质量分别为 和 ,A右端和B左端分别放置物块C、D,物块质量均为 ,A和C以相同速度 向右运动,B和D以相同速度 向左运动,在某时刻发生碰撞,作用时间极短,碰撞后C与D粘在一起形成一个新滑块,A与B粘在一起形成一个新滑板,物块与滑板之间的动摩擦因数均为 。重力加速度大小取 。
 (1)、若 ,求碰撞后瞬间新物块和新滑板各自速度的大小和方向;(2)、若k=0.5 ,从碰撞后到新滑块与新滑板相对静止时,求两者相对位移的大小。17. 打桩机是基建常用工具。某种简易打桩机模型如图所示,重物A、B和C通过不可伸长的轻质长绳跨过两个光滑的等高小定滑轮连接,C与滑轮等高(图中实线位置)时,C到两定滑轮的距离均为L。重物A和B的质量均为m,系统可以在如图虚线位置保持静止,此时连接C的绳与水平方向的夹角为60°。某次打桩时,用外力将C拉到图中实线位置,然后由静止释放。设C的下落速度为 时,与正下方质量为2m的静止桩D正碰,碰撞时间极短,碰撞后C的速度为零,D竖直向下运动 距离后静止(不考虑C、D再次相碰)。A、B、C、D均可视为质点。
(1)、若 ,求碰撞后瞬间新物块和新滑板各自速度的大小和方向;(2)、若k=0.5 ,从碰撞后到新滑块与新滑板相对静止时,求两者相对位移的大小。17. 打桩机是基建常用工具。某种简易打桩机模型如图所示,重物A、B和C通过不可伸长的轻质长绳跨过两个光滑的等高小定滑轮连接,C与滑轮等高(图中实线位置)时,C到两定滑轮的距离均为L。重物A和B的质量均为m,系统可以在如图虚线位置保持静止,此时连接C的绳与水平方向的夹角为60°。某次打桩时,用外力将C拉到图中实线位置,然后由静止释放。设C的下落速度为 时,与正下方质量为2m的静止桩D正碰,碰撞时间极短,碰撞后C的速度为零,D竖直向下运动 距离后静止(不考虑C、D再次相碰)。A、B、C、D均可视为质点。 (1)、求C的质量;(2)、若D在运动过程中受到的阻力F可视为恒力,求F的大小;(3)、撤掉桩D,将C再次拉到图中实线位置,然后由静止释放,求A、B、C的总动能最大时C的动能。18. 如图所示,“L”型平板B静置在地面上,小物块A处于平板B上的 点, 点左侧粗糙,右侧光滑。用不可伸长的轻绳将质量为M的小球悬挂在 点正上方的O点,轻绳处于水平拉直状态。将小球由静止释放,下摆至最低点与小物块A发生碰撞,碰后小球速度方向与碰前方向相同,开始做简谐运动(要求摆角小于 ),A以速度 沿平板滑动直至与B右侧挡板发生弹性碰撞。一段时间后,A返回到O点的正下方时,相对于地面的速度减为零,此时小球恰好第一次上升到最高点。已知A的质量 ,B的质量 ,A与B的动摩擦因数 ,B与地面间的动摩擦因数 ,取重力加速度 。整个过程中A始终在B上,所有碰撞时间忽略不计,不计空气阻力,求:
(1)、求C的质量;(2)、若D在运动过程中受到的阻力F可视为恒力,求F的大小;(3)、撤掉桩D,将C再次拉到图中实线位置,然后由静止释放,求A、B、C的总动能最大时C的动能。18. 如图所示,“L”型平板B静置在地面上,小物块A处于平板B上的 点, 点左侧粗糙,右侧光滑。用不可伸长的轻绳将质量为M的小球悬挂在 点正上方的O点,轻绳处于水平拉直状态。将小球由静止释放,下摆至最低点与小物块A发生碰撞,碰后小球速度方向与碰前方向相同,开始做简谐运动(要求摆角小于 ),A以速度 沿平板滑动直至与B右侧挡板发生弹性碰撞。一段时间后,A返回到O点的正下方时,相对于地面的速度减为零,此时小球恰好第一次上升到最高点。已知A的质量 ,B的质量 ,A与B的动摩擦因数 ,B与地面间的动摩擦因数 ,取重力加速度 。整个过程中A始终在B上,所有碰撞时间忽略不计,不计空气阻力,求: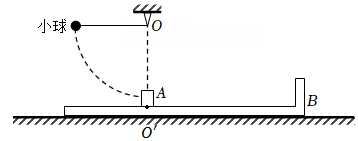 (1)、A与B的挡板碰撞后,二者的速度大小 与 ;(2)、B光滑部分的长度d;(3)、运动过程中A对B的摩擦力所做的功 ;(4)、实现上述运动过程, 的取值范围(结果用 表示)。19. 如图(a),质量为m的篮球从离地H高度处由静止下落,与地面发生一次非弹性碰撞后反弹至离地h的最高处。设篮球在运动过程中所受空气阻力的大小是篮球所受重力的 倍( 为常数且 ),且篮球每次与地面碰撞的碰后速率与碰前速率之比相同,重力加速度大小为g。
(1)、A与B的挡板碰撞后,二者的速度大小 与 ;(2)、B光滑部分的长度d;(3)、运动过程中A对B的摩擦力所做的功 ;(4)、实现上述运动过程, 的取值范围(结果用 表示)。19. 如图(a),质量为m的篮球从离地H高度处由静止下落,与地面发生一次非弹性碰撞后反弹至离地h的最高处。设篮球在运动过程中所受空气阻力的大小是篮球所受重力的 倍( 为常数且 ),且篮球每次与地面碰撞的碰后速率与碰前速率之比相同,重力加速度大小为g。 (1)、求篮球与地面碰撞的碰后速率与碰前速率之比;(2)、若篮球反弹至最高处h时,运动员对篮球施加一个向下的压力F,使得篮球与地面碰撞一次后恰好反弹至h的高度处,力F随高度y的变化如图(b)所示,其中 已知,求 的大小;(3)、篮球从H高度处由静止下落后,每次反弹至最高点时,运动员拍击一次篮球(拍击时间极短),瞬间给其一个竖直向下、大小相等的冲量I,经过N次拍击后篮球恰好反弹至H高度处,求冲量I的大小。20. 某同学受自动雨伞开伞过程的启发,设计了如图12所示的物理模型。竖直放置在水平桌面上的滑杆上套有一个滑块,初始时它们处于静止状态。当滑块从A处以初速度 为 向上滑动时,受到滑杆的摩擦力f为 ,滑块滑到B处与滑杆发生完全非弹性碰撞,带动滑杆离开桌面一起竖直向上运动。已知滑块的质量 ,滑杆的质量 ,A、B间的距离 ,重力加速度g取 ,不计空气阻力。求:
(1)、求篮球与地面碰撞的碰后速率与碰前速率之比;(2)、若篮球反弹至最高处h时,运动员对篮球施加一个向下的压力F,使得篮球与地面碰撞一次后恰好反弹至h的高度处,力F随高度y的变化如图(b)所示,其中 已知,求 的大小;(3)、篮球从H高度处由静止下落后,每次反弹至最高点时,运动员拍击一次篮球(拍击时间极短),瞬间给其一个竖直向下、大小相等的冲量I,经过N次拍击后篮球恰好反弹至H高度处,求冲量I的大小。20. 某同学受自动雨伞开伞过程的启发,设计了如图12所示的物理模型。竖直放置在水平桌面上的滑杆上套有一个滑块,初始时它们处于静止状态。当滑块从A处以初速度 为 向上滑动时,受到滑杆的摩擦力f为 ,滑块滑到B处与滑杆发生完全非弹性碰撞,带动滑杆离开桌面一起竖直向上运动。已知滑块的质量 ,滑杆的质量 ,A、B间的距离 ,重力加速度g取 ,不计空气阻力。求: (1)、滑块在静止时和向上滑动的过程中,桌面对滑杆支持力的大小 和 ;(2)、滑块碰撞前瞬间的速度大小v;(3)、滑杆向上运动的最大高度h。21. 如图(a),一质量为m的物块A与轻质弹簧连接,静止在光滑水平面上:物块B向A运动, 时与弹簧接触,到 时与弹簧分离,第一次碰撞结束,A、B的 图像如图(b)所示。已知从 到 时间内,物块A运动的距离为 。A、B分离后,A滑上粗糙斜面,然后滑下,与一直在水平面上运动的B再次碰撞,之后A再次滑上斜面,达到的最高点与前一次相同。斜面倾角为 ,与水平面光滑连接。碰撞过程中弹簧始终处于弹性限度内。求
(1)、滑块在静止时和向上滑动的过程中,桌面对滑杆支持力的大小 和 ;(2)、滑块碰撞前瞬间的速度大小v;(3)、滑杆向上运动的最大高度h。21. 如图(a),一质量为m的物块A与轻质弹簧连接,静止在光滑水平面上:物块B向A运动, 时与弹簧接触,到 时与弹簧分离,第一次碰撞结束,A、B的 图像如图(b)所示。已知从 到 时间内,物块A运动的距离为 。A、B分离后,A滑上粗糙斜面,然后滑下,与一直在水平面上运动的B再次碰撞,之后A再次滑上斜面,达到的最高点与前一次相同。斜面倾角为 ,与水平面光滑连接。碰撞过程中弹簧始终处于弹性限度内。求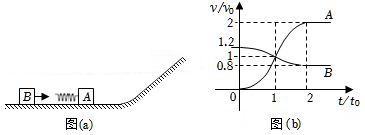 (1)、第一次碰撞过程中,弹簧弹性势能的最大值;(2)、第一次碰撞过程中,弹簧压缩量的最大值;(3)、物块A与斜面间的动摩擦因数。22. 一玩具以初速度 从水平地面竖直向上抛出,达到最高点时,用遥控器将玩具内压缩的轻弹簧弹开,该玩具沿水平方向分裂成质量之比为1∶4的两部分,此时它们的动能之和与玩具从地面抛出时的动能相等。弹簧弹开的时间极短,不计空气阻力。求(1)、玩具上升到最大高度 时的速度大小;(2)、两部分落地时速度大小之比。23. 如图所示,一圆心为O、半径为R的光滑半圆弧轨道固定在竖直平面内,其下端与光滑水平面在Q点相切。在水平面上,质量为m的小物块A以某一速度向质量也为m的静止小物块B运动。A、B发生正碰后,B到达半圆弧轨道最高点时对轨道压力恰好为零,A沿半圆弧轨道运动到与O点等高的C点时速度为零。已知重力加速度大小为g,忽略空气阻力。
(1)、第一次碰撞过程中,弹簧弹性势能的最大值;(2)、第一次碰撞过程中,弹簧压缩量的最大值;(3)、物块A与斜面间的动摩擦因数。22. 一玩具以初速度 从水平地面竖直向上抛出,达到最高点时,用遥控器将玩具内压缩的轻弹簧弹开,该玩具沿水平方向分裂成质量之比为1∶4的两部分,此时它们的动能之和与玩具从地面抛出时的动能相等。弹簧弹开的时间极短,不计空气阻力。求(1)、玩具上升到最大高度 时的速度大小;(2)、两部分落地时速度大小之比。23. 如图所示,一圆心为O、半径为R的光滑半圆弧轨道固定在竖直平面内,其下端与光滑水平面在Q点相切。在水平面上,质量为m的小物块A以某一速度向质量也为m的静止小物块B运动。A、B发生正碰后,B到达半圆弧轨道最高点时对轨道压力恰好为零,A沿半圆弧轨道运动到与O点等高的C点时速度为零。已知重力加速度大小为g,忽略空气阻力。 (1)、求B从半圆弧轨道飞出后落到水平面的位置到Q点的距离;(2)、当A由C点沿半圆弧轨道下滑到D点时,OD与OQ夹角为θ,求此时A所受力对A做功的功率;(3)、求碰撞过程中A和B损失的总动能。24. 算盘是我国古老的计算工具,中心带孔的相同算珠可在算盘的固定导杆上滑动,使用前算珠需要归零,如图所示,水平放置的算盘中有甲、乙两颗算珠未在归零位置,甲靠边框b,甲、乙相隔 ,乙与边框a相隔 ,算珠与导杆间的动摩擦因数 。现用手指将甲以 的初速度拨出,甲、乙碰撞后甲的速度大小为 ,方向不变,碰撞时间极短且不计,重力加速度g取 。
(1)、求B从半圆弧轨道飞出后落到水平面的位置到Q点的距离;(2)、当A由C点沿半圆弧轨道下滑到D点时,OD与OQ夹角为θ,求此时A所受力对A做功的功率;(3)、求碰撞过程中A和B损失的总动能。24. 算盘是我国古老的计算工具,中心带孔的相同算珠可在算盘的固定导杆上滑动,使用前算珠需要归零,如图所示,水平放置的算盘中有甲、乙两颗算珠未在归零位置,甲靠边框b,甲、乙相隔 ,乙与边框a相隔 ,算珠与导杆间的动摩擦因数 。现用手指将甲以 的初速度拨出,甲、乙碰撞后甲的速度大小为 ,方向不变,碰撞时间极短且不计,重力加速度g取 。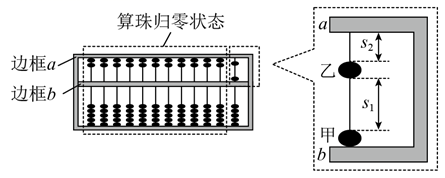 (1)、通过计算,判断乙算珠能否滑动到边框a;(2)、求甲算珠从拨出到停下所需的时间。25. 如图,一长木板在光滑的水平面上以速度v0向右做匀速直线运动,将一小滑块无初速地轻放在木板最右端。已知滑块和木板的质量分别为m和2m,它们之间的动摩擦因数为μ,重力加速度为g。
(1)、通过计算,判断乙算珠能否滑动到边框a;(2)、求甲算珠从拨出到停下所需的时间。25. 如图,一长木板在光滑的水平面上以速度v0向右做匀速直线运动,将一小滑块无初速地轻放在木板最右端。已知滑块和木板的质量分别为m和2m,它们之间的动摩擦因数为μ,重力加速度为g。 (1)、滑块相对木板静止时,求它们的共同速度大小;(2)、某时刻木板速度是滑块的2倍,求此时滑块到木板最右端的距离;(3)、若滑块轻放在木板最右端的同时,给木板施加一水平向右的外力,使得木板保持匀速直线运动,直到滑块相对木板静止,求此过程中滑块的运动时间以及外力所做的功。26. 如图,一滑雪道由 和 两段滑道组成,其中 段倾角为 , 段水平, 段和 段由一小段光滑圆弧连接,一个质量为 的背包在滑道顶端A处由静止滑下,若 后质量为 的滑雪者从顶端以 的初速度、 的加速度匀加速追赶,恰好在坡底光滑圆弧的水平处追上背包并立即将其拎起,背包与滑道的动摩擦因数为 ,重力加速度取 , , ,忽略空气阻力及拎包过程中滑雪者与背包的重心变化,求:
(1)、滑块相对木板静止时,求它们的共同速度大小;(2)、某时刻木板速度是滑块的2倍,求此时滑块到木板最右端的距离;(3)、若滑块轻放在木板最右端的同时,给木板施加一水平向右的外力,使得木板保持匀速直线运动,直到滑块相对木板静止,求此过程中滑块的运动时间以及外力所做的功。26. 如图,一滑雪道由 和 两段滑道组成,其中 段倾角为 , 段水平, 段和 段由一小段光滑圆弧连接,一个质量为 的背包在滑道顶端A处由静止滑下,若 后质量为 的滑雪者从顶端以 的初速度、 的加速度匀加速追赶,恰好在坡底光滑圆弧的水平处追上背包并立即将其拎起,背包与滑道的动摩擦因数为 ,重力加速度取 , , ,忽略空气阻力及拎包过程中滑雪者与背包的重心变化,求: (1)、滑道AB段的长度;(2)、滑雪者拎起背包时这一瞬间的速度。27. 如图所示,水平地面上有一高 的水平台面,台面上竖直放置倾角 的粗糙直轨道 、水平光滑直轨道 、四分之一圆周光滑细圆管道 和半圆形光滑轨道 ,它们平滑连接,其中管道 的半径 、圆心在 点,轨道 的半径 、圆心在 点, 、D、 和F点均处在同一水平线上。小滑块从轨道 上距台面高为h的P点静止下滑,与静止在轨道 上等质量的小球发生弹性碰撞,碰后小球经管道 、轨道 从F点竖直向下运动,与正下方固定在直杆上的三棱柱G碰撞,碰后速度方向水平向右,大小与碰前相同,最终落在地面上Q点,已知小滑块与轨道 间的动摩擦因数 , , 。(1)、若小滑块的初始高度 ,求小滑块到达B点时速度 的大小;(2)、若小球能完成整个运动过程,求h的最小值 ;(3)、若小球恰好能过最高点E,且三棱柱G的位置上下可调,求落地点Q与F点的水平距离x的最大值 。
(1)、滑道AB段的长度;(2)、滑雪者拎起背包时这一瞬间的速度。27. 如图所示,水平地面上有一高 的水平台面,台面上竖直放置倾角 的粗糙直轨道 、水平光滑直轨道 、四分之一圆周光滑细圆管道 和半圆形光滑轨道 ,它们平滑连接,其中管道 的半径 、圆心在 点,轨道 的半径 、圆心在 点, 、D、 和F点均处在同一水平线上。小滑块从轨道 上距台面高为h的P点静止下滑,与静止在轨道 上等质量的小球发生弹性碰撞,碰后小球经管道 、轨道 从F点竖直向下运动,与正下方固定在直杆上的三棱柱G碰撞,碰后速度方向水平向右,大小与碰前相同,最终落在地面上Q点,已知小滑块与轨道 间的动摩擦因数 , , 。(1)、若小滑块的初始高度 ,求小滑块到达B点时速度 的大小;(2)、若小球能完成整个运动过程,求h的最小值 ;(3)、若小球恰好能过最高点E,且三棱柱G的位置上下可调,求落地点Q与F点的水平距离x的最大值 。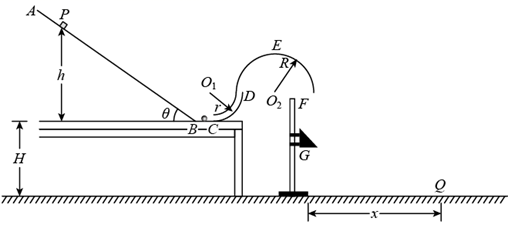 28. 在一柱形区域内有匀强电场,柱的横截面积是以O为圆心,半径为R的圆,AB为圆的直径,如图所示。质量为m,电荷量为q(q>0)的带电粒子在纸面内自A点先后以不同的速度进入电场,速度方向与电场的方向垂直。已知刚进入电场时速度为零的粒子,自圆周上的C点以速率v0穿出电场,AC与AB的夹角θ=60°。运动中粒子仅受电场力作用。
28. 在一柱形区域内有匀强电场,柱的横截面积是以O为圆心,半径为R的圆,AB为圆的直径,如图所示。质量为m,电荷量为q(q>0)的带电粒子在纸面内自A点先后以不同的速度进入电场,速度方向与电场的方向垂直。已知刚进入电场时速度为零的粒子,自圆周上的C点以速率v0穿出电场,AC与AB的夹角θ=60°。运动中粒子仅受电场力作用。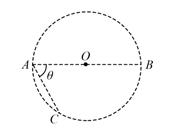 (1)、求电场强度的大小;(2)、为使粒子穿过电场后的动能增量最大,该粒子进入电场时的速度应为多大?(3)、为使粒子穿过电场前后动量变化量的大小为mv0 , 该粒子进入电场时的速度应为多大?29. 长为l的轻绳上端固定,下端系着质量为 的小球A,处于静止状态。A受到一个水平瞬时冲量后在竖直平面内做圆周运动,恰好能通过圆周轨迹的最高点。当A回到最低点时,质量为 的小球B与之迎面正碰,碰后A、B粘在一起,仍做圆周运动,并能通过圆周轨迹的最高点。不计空气阻力,重力加速度为g,求(1)、A受到的水平瞬时冲量I的大小;(2)、碰撞前瞬间B的动能 至少多大?30. 如图所示,一倾角为 的固定斜面的底端安装一弹性挡板,P、Q两物块的质量分别为m和4m,Q静止于斜面上A处。某时刻,P以沿斜面向上的速度v0与Q发生弹性碰撞。Q与斜面间的动摩擦因数等于 ,设最大静摩擦力等于滑动摩擦力。P与斜面间无摩擦,与挡板之间的碰撞无动能损失。两物块均可以看作质点,斜面足够长,Q的速度减为零之前P不会与之发生碰撞。重力加速度大小为g。
(1)、求电场强度的大小;(2)、为使粒子穿过电场后的动能增量最大,该粒子进入电场时的速度应为多大?(3)、为使粒子穿过电场前后动量变化量的大小为mv0 , 该粒子进入电场时的速度应为多大?29. 长为l的轻绳上端固定,下端系着质量为 的小球A,处于静止状态。A受到一个水平瞬时冲量后在竖直平面内做圆周运动,恰好能通过圆周轨迹的最高点。当A回到最低点时,质量为 的小球B与之迎面正碰,碰后A、B粘在一起,仍做圆周运动,并能通过圆周轨迹的最高点。不计空气阻力,重力加速度为g,求(1)、A受到的水平瞬时冲量I的大小;(2)、碰撞前瞬间B的动能 至少多大?30. 如图所示,一倾角为 的固定斜面的底端安装一弹性挡板,P、Q两物块的质量分别为m和4m,Q静止于斜面上A处。某时刻,P以沿斜面向上的速度v0与Q发生弹性碰撞。Q与斜面间的动摩擦因数等于 ,设最大静摩擦力等于滑动摩擦力。P与斜面间无摩擦,与挡板之间的碰撞无动能损失。两物块均可以看作质点,斜面足够长,Q的速度减为零之前P不会与之发生碰撞。重力加速度大小为g。 (1)、求P与Q第一次碰撞后瞬间各自的速度大小vP1、vQ1;(2)、求第n次碰撞使物块Q上升的高度hn;(3)、求物块Q从A点上升的总高度H;(4)、为保证在Q的速度减为零之前P不会与之发生碰撞,求A点与挡板之间的最小距离s。
(1)、求P与Q第一次碰撞后瞬间各自的速度大小vP1、vQ1;(2)、求第n次碰撞使物块Q上升的高度hn;(3)、求物块Q从A点上升的总高度H;(4)、为保证在Q的速度减为零之前P不会与之发生碰撞,求A点与挡板之间的最小距离s。