(人教版)2022-2023学年度第一学期八年级数学第12章 全等三角形 同步测试
试卷更新日期:2022-07-08 类型:同步测试
一、单选题
-
1. 如图所示, ≌ ,下面四个结论中,不一定成立的是( ).
 A、 和 的面积相等 B、 和 的周长相等 C、 D、2. 已知图中的两个三角形全等,则 等于( )
A、 和 的面积相等 B、 和 的周长相等 C、 D、2. 已知图中的两个三角形全等,则 等于( ) A、 B、 C、 D、3. 如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD , 正方形EFGH , 正方形MNPQ的面积分别为S1 , S2 , S3 , 若S1+S2+S3=60,则S2的值是( )
A、 B、 C、 D、3. 如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD , 正方形EFGH , 正方形MNPQ的面积分别为S1 , S2 , S3 , 若S1+S2+S3=60,则S2的值是( ) A、12 B、15 C、20 D、254. 如图,在△DEC和△BFA中,点A,E,F,C在同一直线上,已知AB∥CD,且AB=CD,若利用“ASA”证明△DEC≌△BFA,则需添加的条件是( )
A、12 B、15 C、20 D、254. 如图,在△DEC和△BFA中,点A,E,F,C在同一直线上,已知AB∥CD,且AB=CD,若利用“ASA”证明△DEC≌△BFA,则需添加的条件是( ) A、EC=FA B、∠A=∠C C、∠D=∠B D、BF=DE5. 将三根木条钉成一个三角形木架,这个三角形木架具有稳定性.解释这个现象的数学原理是( )A、SSS B、SAS C、ASA D、AAS6. 如图,已知AC=DB,添加下列条件,仍不能判断△ABC≌△DCB的是( )
A、EC=FA B、∠A=∠C C、∠D=∠B D、BF=DE5. 将三根木条钉成一个三角形木架,这个三角形木架具有稳定性.解释这个现象的数学原理是( )A、SSS B、SAS C、ASA D、AAS6. 如图,已知AC=DB,添加下列条件,仍不能判断△ABC≌△DCB的是( )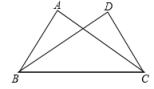 A、∠A=∠D=90° B、∠ABC=∠DCB C、∠ACB=∠DBC D、AB=DC7. 如图,已知∠1=∠2,要说明△ABD≌△ACD,还需从下列条件中选一个,不正确的选法是( )
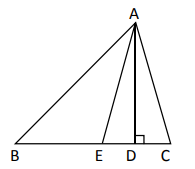
A、∠A=∠D=90° B、∠ABC=∠DCB C、∠ACB=∠DBC D、AB=DC7. 如图,已知∠1=∠2,要说明△ABD≌△ACD,还需从下列条件中选一个,不正确的选法是( ) A、∠ADB=∠ADC B、∠B=∠C C、DB=DC D、AB=AC8. 如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D.若S△ACD=6,AC=6,则点D到AB的距离为( )
A、∠ADB=∠ADC B、∠B=∠C C、DB=DC D、AB=AC8. 如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D.若S△ACD=6,AC=6,则点D到AB的距离为( ) A、1 B、2 C、3 D、49. 如图, AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC长是( )
A、1 B、2 C、3 D、49. 如图, AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC长是( ) A、6 B、5 C、4 D、310. 如图,已知 , 求作射线 , 使平分 , 那么作法的合理顺序是( )
A、6 B、5 C、4 D、310. 如图,已知 , 求作射线 , 使平分 , 那么作法的合理顺序是( )①作射线;②在射线和上分别截取、 , 使;③分别以、为圆心,大于的长为半径在内作弧,两弧交于点 .
 A、①②③ B、②①③ C、②③① D、③①②
A、①②③ B、②①③ C、②③① D、③①②二、填空题
-
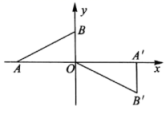
11. 如图,在平面直角坐标系中,的顶点坐标分别是 , 若点在x轴上,则点的坐标是 .
 12. 如图,在△ABC和△DEF中,∠B=∠DEF,∠A=∠D,请你添加一个条件 , 使△ABC≌△DEF(图形中不再增加其他字母).
12. 如图,在△ABC和△DEF中,∠B=∠DEF,∠A=∠D,请你添加一个条件 , 使△ABC≌△DEF(图形中不再增加其他字母).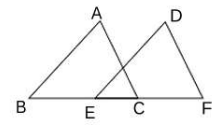 13. 如图,A,B两点分别位于一个假山的两端,小明想用绳子测量A、B间的距离,首先在地面上取一个可以直接到达A点和B点的点C,连接AC并延长到点D,使CD=AC,连接BC并延长到点E,使CE=CB,连接DE并测量出它的长度为8m,则AB间的距离为 .
13. 如图,A,B两点分别位于一个假山的两端,小明想用绳子测量A、B间的距离,首先在地面上取一个可以直接到达A点和B点的点C,连接AC并延长到点D,使CD=AC,连接BC并延长到点E,使CE=CB,连接DE并测量出它的长度为8m,则AB间的距离为 . 14. 如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,DF⊥AC于点F,S△ABC=21,DE=3,AB=9,则AC长是 .
14. 如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,DF⊥AC于点F,S△ABC=21,DE=3,AB=9,则AC长是 . 15. 如图,在△ABC中,∠C=90°,AD平分∠BAC,点D到AB的距离为7cm,CD=cm.
15. 如图,在△ABC中,∠C=90°,AD平分∠BAC,点D到AB的距离为7cm,CD=cm.
三、解答题
-
16. 如图,AB=AD,BC=DC,点E在AC上.求证:BE=DE.
 17. 如图,已知∆ABE≌∆ACD , 求证:∠BAD=∠CAE .
17. 如图,已知∆ABE≌∆ACD , 求证:∠BAD=∠CAE . 18. 如图,AD与BC相交于点O,AB=CD, , EB=ED,求证: .
18. 如图,AD与BC相交于点O,AB=CD, , EB=ED,求证: . 19. 如图,已知∠A=∠C,AE、CF分别与BD交于点E、F.请你从下面三项中再选出两个作为条件,另一个作为结论,写出一个真命题,并加以证明.①AB∥DC;②AE∥CF;③DE=BF.
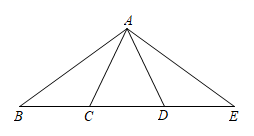
19. 如图,已知∠A=∠C,AE、CF分别与BD交于点E、F.请你从下面三项中再选出两个作为条件,另一个作为结论,写出一个真命题,并加以证明.①AB∥DC;②AE∥CF;③DE=BF. 20. 如图,点C、D在BE上,BC=ED,AC=AD,求证:AB=AE.
20. 如图,点C、D在BE上,BC=ED,AC=AD,求证:AB=AE.