(人教版)2022-2023学年度第一学期八年级数学12.3角的平分线的性质 同步测试
试卷更新日期:2022-07-08 类型:同步测试
一、单选题
-
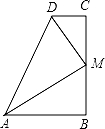
1. 点P在∠AOB的平分线上(不与点O重合),PC⊥OA于点C,D是OB边上任意一点,连接PD.若PC=3,则下列关于线段PD的说法一定正确的是( )A、PD=PO B、PD<3 C、存在无数个点D使得PD=PC D、PD≥32. 如图所示,P为平分线上的点,于D, , 则点P到OB的距离为( )
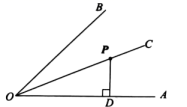 A、5cm B、4cm C、3cm D、2cm3. 如图,Rt△ABC中,B=90,点P在边AB上,CP平分∠ACB,PB=3cm,AC=10cm,则△APC的面积是( )
A、5cm B、4cm C、3cm D、2cm3. 如图,Rt△ABC中,B=90,点P在边AB上,CP平分∠ACB,PB=3cm,AC=10cm,则△APC的面积是( ) A、15cm2 B、22.5cm2 C、30cm2 D、45cm24. 如图,在等腰中, , , BD平分 , 交AC于点D, , 若cm,则的周长为( )
A、15cm2 B、22.5cm2 C、30cm2 D、45cm24. 如图,在等腰中, , , BD平分 , 交AC于点D, , 若cm,则的周长为( ) A、8cm B、10cm C、12cm D、14cm5. 如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,∠ACB的平分线与∠ABC的外角的平分线交于E点,连接AE,则∠AEC的度数是( )
A、8cm B、10cm C、12cm D、14cm5. 如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,∠ACB的平分线与∠ABC的外角的平分线交于E点,连接AE,则∠AEC的度数是( ) A、45° B、40° C、35° D、30°6. 如图,点O在内,且到三边的距离相等,∠A=64°,则∠BOC的度数为( )
A、45° B、40° C、35° D、30°6. 如图,点O在内,且到三边的距离相等,∠A=64°,则∠BOC的度数为( ) A、58° B、64° C、122° D、124°7. 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画圆弧,分别交AB、AC于点D、E,再分别以点D、E为圆心,大于DE长为半径画圆弧,两弧交于点F,作射线AF交边BC于点G,若CG=3,AB=10,则△ABG的面积是( )
A、58° B、64° C、122° D、124°7. 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画圆弧,分别交AB、AC于点D、E,再分别以点D、E为圆心,大于DE长为半径画圆弧,两弧交于点F,作射线AF交边BC于点G,若CG=3,AB=10,则△ABG的面积是( ) A、3 B、10 C、15 D、308. 如图,直线l1、l2、l3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则供选择的地址有( )
A、3 B、10 C、15 D、308. 如图,直线l1、l2、l3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则供选择的地址有( )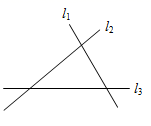 A、1处 B、2处 C、3处 D、4处9. 用两把完全相同的长方形直尺按如图方式摆放,一把直尺压住射线OB交射线OA于点M,另一把直尺压住射线OA交第一把直尺于点P,作射线OP.若∠BOP=28°,则∠AMP的大小为( )
A、1处 B、2处 C、3处 D、4处9. 用两把完全相同的长方形直尺按如图方式摆放,一把直尺压住射线OB交射线OA于点M,另一把直尺压住射线OA交第一把直尺于点P,作射线OP.若∠BOP=28°,则∠AMP的大小为( )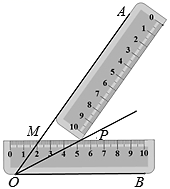 A、46° B、52° C、56° D、62°10. 如图,若OP平分 , , , 垂足分别是C、D,则下列结论中错误的是
A、46° B、52° C、56° D、62°10. 如图,若OP平分 , , , 垂足分别是C、D,则下列结论中错误的是 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,在锐角三角形ABC中,AB=4,△ABC的面积为10,BD平分∠ABC,若M、N分别是BD、BC上的动点,则CM+MN的最小值为
 12. 小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”小明的做法,其理论依据是
12. 小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”小明的做法,其理论依据是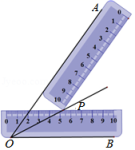 13. 如图,在中,AD是的平分线, , , 则 .
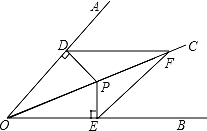
13. 如图,在中,AD是的平分线, , , 则 . 14. 如图,在中,AD为BC边上的中线,于点E,AD与CE交于点F,连接BF.若BF平分 , , , 则的面积为 .
14. 如图,在中,AD为BC边上的中线,于点E,AD与CE交于点F,连接BF.若BF平分 , , , 则的面积为 . 15. 如图,在中, , 三角形的两个外角和的平分线交于点E.则 .
15. 如图,在中, , 三角形的两个外角和的平分线交于点E.则 .
三、解答题
-
16. 如图,点D、B分别在∠A的两边上,C是∠A内一点,AB = AD,BC = CD,CE⊥AD于E,CF⊥AF于F.求证:CE = CF.
 17. 如图,CE是 ABC的外角∠ACD的平分线,且CE交BA的延长线于点E,AF是△ABC的高,∠B=30°,∠E=40°,求∠ECD和∠FAC的度数.
17. 如图,CE是 ABC的外角∠ACD的平分线,且CE交BA的延长线于点E,AF是△ABC的高,∠B=30°,∠E=40°,求∠ECD和∠FAC的度数. 18. 如图,∠ABC=∠DCB,BD、CA分别平分∠ABC、∠DCB.求证:AC=DB.
18. 如图,∠ABC=∠DCB,BD、CA分别平分∠ABC、∠DCB.求证:AC=DB. 19. 已知:如图,AD是△ABC的角平分线,DE∥AC,DE交AB于点E,DF∥AB,DF交AC于点F.求证:DA平分∠EDF.
19. 已知:如图,AD是△ABC的角平分线,DE∥AC,DE交AB于点E,DF∥AB,DF交AC于点F.求证:DA平分∠EDF. 20. 如图,在 中,D是 边的中点, 于点E , 于点F , 且 .
20. 如图,在 中,D是 边的中点, 于点E , 于点F , 且 .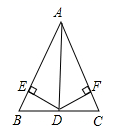
求证: 平分 .