（人教版）2022-2023学年度第一学期八年级数学12.1全等三角形 同步测试
试卷更新日期：2022-07-08 类型：同步测试
一、单选题
-
1. 如图，点 ， 在 的边 上， ≌ ，其中 ， 为对应顶点， ， 为对应顶点，下列结论不一定成立的是（ ）
A、 B、 C、 D、2. 如图，点D在AC上，点B在AE上， ABC≌ DBE ． 若∠A：∠C=5：3，则∠DBC的度数为（ ）
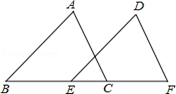
A、12° B、24° C、20° D、36°3. 如图 ABC≌ ，边 过点A且平分∠BAC交BC于点D ， ∠B=26°， =94°，则 的度数为（ ）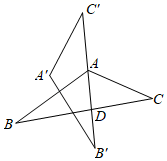
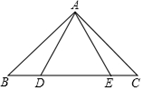
A、34° B、40° C、45° D、60°4. 如图， ABC≌ DEC ， B ， C ， D三点在同一直线上，若CE=6，AC=9，则BD的长为（ ）
A、3 B、9 C、12 D、155. 如图，已知△ABC中，AB=AC=24cm，∠B=∠C ， BC=16cm，点D为AB的中点，如果点P在线段BC上以4cm/s的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动，当点Q的运动速度为（ ）cm/s时，能够在某一时刻使△BPD与△CQP全等．
A、4 B、3 C、4或3 D、4或66. 如图，△ABC≌△AED ， 点E在线段BC上，∠1＝44°，则∠AED的大小为（ ）
A、70° B、68° C、64° D、62°7. 如图，△ABC≌△DEC，B、C、D在同一直线上，且CE＝5，AC＝7，则BD长（ ）
A、12 B、7 C、2 D、148. 下列图形是全等图形的是（ ）A、
B、
C、
D、
9. 如图，已知 ，下列结论中错误的是（ ）
A、 B、 C、 D、10. 如图，若△ABC≌△DEF，EF=8， EC=5，则BE的长为（ ）
A、1 B、2 C、3 D、4二、填空题
-
11. 在平面直角坐标系中，已知 ， ， ， 若 ， 则点D的坐标为.12. 如图，△ABC≌△DEF，若∠A=65° ，则∠EDC的度数为.
13. 如图是两个全等的三角形，图中字母表示三角形的边长，则∠的度数为°.
14. 如图，在平面直角坐标系xOy中，点A（-3，0），B（3，0），C（3，2），如果△ABC与△ABD全等，那么点D的坐标可以是（写出一个即可）．
15. 如图，在中， ， 一条线段 ， P，Q两点分别在线段和的垂线上移动，若以A、B、C为顶点的三角形与以A、P、Q为顶点的三角形全等，则的长为 ．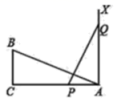
三、解答题
-
16. 如图，点C在线段BD上，AB⊥BD于B，ED⊥BD于D，∠ACE＝90°.如果AC＝5cm，CE＝6cm；点P以2cm/s的速度沿A→C→E向终点E运动，同时点Q以3cm/s的速度从E开始，在线段EC上往返运动（即沿E→C→E→C→…运动），当点P到达终点时，P、Q同时停止运动.过P、Q分别作BD的垂线，垂足为M、N.设运动时间为ts，当以P、C、M为顶点的三角形与△QCN全等时，求t的值.
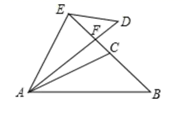
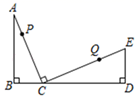17. 如图，△ABO≌△CDO，点B在CD上，AO∥CD，∠BOD＝30°，求∠A的度数．
18. 如图， ， ， ，求 的度数．
19. 如图，△EFG≌△NMH，E，H，G，N在同一条直线上，EF和NM，FG和MH是对应边，若EH＝1.1cm，NH＝3.3cm．求线段HG的长．
20. 已知：如图，在△AOB和△COD中，OA=OB，OC=OD．，若∠AOB=∠COD=60°，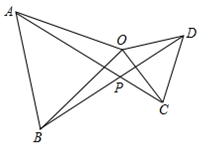
①求证：AC=BD；
②求∠APB的度数．
