2022年高考数学真题分类汇编专题06：数列

试卷更新日期：2022-07-07 类型：二轮复习

进入出卷网下载

一、单选题

1. 已知数列 ${a_{n}}$ 满足 $a_{1} = 1 ， a_{n + 1} = a_{n} - \frac{1}{3} a_{n}^{2} (n \in N^{*})$ ，则（）

A、 $2 < 100 a_{100} < \frac{5}{2}$ B、 $\frac{5}{2} < 100 a_{100} < 3$ C、 $3 < 100 a_{100} < \frac{7}{2}$ D、 $\frac{7}{2} < 100 a_{100} < 4$

查看试题解析
2. 中国的古建筑不仅是挡风遮雨的住处，更是美学和哲学的体现．如图是某古建筑物的剖面图， $D D_{1} ， C C_{1} ， B B_{1} ， A A_{1}$ 是举， $O D_{1} ， D C_{1} ， C B_{1} ， B A_{1}$ 是相等的步，相邻桁的举步之比分别为 $\frac{D D_{1}}{O D_{1}} = 0.5 ， \frac{C C_{1}}{D C_{1}} = k_{1} ， \frac{B B_{1}}{C B_{1}} = k_{2} ， \frac{A A_{1}}{B A_{1}} = k_{3}$ ，若 $k_{1} ， k_{2} ， k_{3}$ 是公差为0.1的等差数列，且直线 $O A$ 的斜率为0.725，则 $k_{3} =$ （）

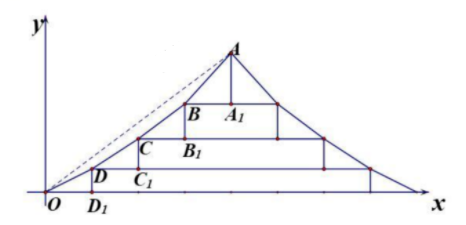A、0.75 B、0.8 C、0.85 D、0.9

查看试题解析
3. 已知等比数列 ${a_{n}}$ 的前3项和为168， $a_{2} - a_{5} = 42$ ，则 $a_{6} =$ （）

A、14 B、12 C、6 D、3

查看试题解析
4. 嫦娥二号卫星在完成探月任务后，继续进行深空探测，成为我国第一颗环绕太阳飞行的人造行星，为研究嫦娥二号绕日周期与地球绕日周期的比值，用到数列 ${b_{n}}$ ： $b_{1} = 1 + \frac{1}{α_{1}}$ ， $b_{2} = 1 + \frac{1}{α_{1} + \frac{1}{α_{2}}}$ ， $b_{3} = 1 + \frac{1}{α_{1} + \frac{1}{α_{2} + \frac{1}{α_{3}}}}$ ，…，依此类推，其中 $α_{k} \in N^{*} (k = 1 ， 2 ， \dots)$ ．则（）

A、 $b_{1} < b_{5}$ B、 $b_{3} < b_{8}$ C、 $b_{6} < b_{2}$ D、 $b_{4} < b_{7}$

查看试题解析
5. 通过以下操作得到一系列数列：第1次，在2，3之间插入2与3的积6，得到数列2，6，3；第2次，在2，6，3每两个相邻数之间插入它们的积，得到数列2，12，6，18，3；类似地，第3次操作后，得到数列：2，24，12，72，6，108，18，54，3.按上述这样操作11次后，得到的数列记为 ${a_{n}}$ ，则 $a_{1025}$ 的值是（）

A、6 B、12 C、18 D、108

查看试题解析
6. 已知 ${a_{n}}$ 为等比数列， ${a_{n}}$ 的前n项和为 $S_{n}$ ，前n项积为 $T_{n}$ ，则下列选项中正确的是（）

A、若 $S_{2022} > S_{2021}$ ，则数列 ${a_{n}}$ 单调递增 B、若 $T_{2022} > T_{2021}$ ，则数列 ${a_{n}}$ 单调递增 C、若数列 ${S_{n}}$ 单调递增，则 $a_{2022} \geq a_{2021}$ D、若数列 ${T_{n}}$ 单调递增，则 $a_{2022} \geq a_{2021}$

查看试题解析

二、填空题

7. 记 $S_{n}$ 为等差数列 ${a_{n}}$ 的前n项和．若 $2 S_{3} = 3 S_{2} + 6$ ，则公差 $d =$ ．

查看试题解析
8. 已知数列 ${a_{n}}$ 的各项均为正数，其前 $n$ 项和 $S_{n}$ ，满足 $a_{n} \cdot S_{n} = 9 (n = 1 ， 2 ， \dots)$ 给出下列四个结论：
① ${a_{n}}$ 的第2项小于3； ② ${a_{n}}$ 为等比数列；

③ ${a_{n}}$ 为递减数列； ④ ${a_{n}}$ 中存在小于 $\frac{1}{100}$ 的项。

其中所有正确结论的序号是．

查看试题解析
9. 若数列 ${a_{n}}$ 通项公式为 $a_{n} = 2 n$ ，记前n项和为 $S_{n}$ ，则 $a_{2} =$ ； $S_{4} =$ .

查看试题解析

三、解答题

10. 已知等差数列 ${a_{n}}$ 的首项 $a_{1} = - 1$ ，公差 $d > 1$ ．记 ${a_{n}}$ 的前n项和为 $S_{n} (n \in N^{*})$ ．
（Ⅰ）若 $S_{4} - 2 a_{2} a_{3} + 6 = 0$ ，求 $S_{n}$ ；

（Ⅱ）若对于每个 $n \in N^{*}$ ，存在实数 $c_{n}$ ，使 $a_{n} + c_{n} ， a_{n + 1} + 4 c_{n} ， a_{n + 2} + 15 c_{n}$ 成等比数列，求d的取值范围．

查看试题解析
11. 已知 ${a_{n}}$ 为等差数列， ${b_{n}}$ 是公比为2的等比数列，且 $a_{2} - b_{2} = a_{3} - b_{3} = b_{4} - a_{4}$ ．

(1)、证明： $a_{1} = b_{1}$ ；

(2)、求集合 ${k | b_{k} = a_{m} + a_{1} ， 1 \leq m \leq 500}$ 中元素个数．

查看试题解析
12. 记 $S_{n}$ 为数列 ${a_{n}}$ 的前n项和．已知 $\frac{2 S_{n}}{n} + n = 2 a_{n} + 1$ ．

(1)、证明： ${a_{n}}$ 是等差数列；

(2)、若 $a_{4} ， a_{7} ， a_{9}$ 成等比数列，求 $S_{n}$ 的最小值．

查看试题解析
13. 已知 $Q ： a_{1} ， a_{2} ， \dots ， a_{k}$ 为有穷整数数列．给定正整数 $m$ ，若对任意的 $n \in {1 ， 2 ， \dots ， m}$ ，在 $Q$ 中存在 $a_{1} ， a_{i + 1} ， a_{i + 2} ， \dots ， a_{i + j} (j ⩾ 0)$ ，使得 $a_{i} + a_{i + 1} + a_{i + 2} + \dots + a_{i + j} = n$ ，则称 $Q$ 为 $m -$ 连续可表数列．
（Ⅰ）判断 $Q ： 2 ， 1 ， 4$ 是否为5-连续可表数列？是否为 $6 -$ 连续可表数列？说明理由；

（Ⅱ）若 $Q ： a_{1} ， a_{2} ， \dots ， a_{k}$ 为 $8 -$ 连续可表数列，求证： $k$ 的最小值为4；

（Ⅲ）若 $Q ： a_{1} ， a_{2} ， \dots ， a_{k}$ 为 $20 -$ 连续可表数列， $a_{1} + a_{2} + \dots + a_{k} < 20$ ，求证： $k \geq 7$ ．

查看试题解析
14. 记 $S_{n}$ 为数列 ${a_{n}}$ 的前n项和，已知 $a_{1} = 1 ， {\frac{S_{n}}{a_{n}}}$ 是公差为 $\frac{1}{3}$ ，的等差数列.

(1)、求 ${a_{n}}$ 的通项公式；

(2)、证明： $\frac{1}{a_{1}} + \frac{1}{a_{2}} + \dots + \frac{1}{a_{n}} < 2$

查看试题解析
15. 已知函数 $f (x) = e^{x} - a x$ 和 $g (x) = a x - ln x$ 有相同的最小值.

(1)、求a；

(2)、证明：存在直线 $y = b ，$ ，其与两条曲线 $y = f (x)$ 和 $y = g (x)$ 共有三个不同的交点，并且从左到右的三个交点的横坐标成等差数列．

查看试题解析
16. 已知数列 ${a_{n}}$ ， $a_{2} = 1$ ， ${a_{n}}$ 的前n项和为 $S_{n}$ .

(1)、若 ${a_{n}}$ 为等比数列， $S_{2} = 3$ ，求 $\lim_{n \to \infty} S_{n}$ ；

(2)、若 ${a_{n}}$ 为等差数列，公差为d，对任意 $n \in N^{*}$ ，均满足 $S_{2 n} \geq n$ ，求d的取值范围.

查看试题解析