2022年高考数学真题分类汇编专题05:不等式
试卷更新日期:2022-07-07 类型:二轮复习
一、单选题
-
1. 若实数x,y满足约束条件 则 的最大值是( )A、20 B、18 C、13 D、62. 若x , y满足约束条件 则 的最大值是( )A、 B、4 C、8 D、123. 设全集 ,集合 ,则 ( )A、 B、 C、 D、4. 已知 ,则( )A、 B、 C、 D、5. 设 则( )A、 B、 C、 D、6. 若集合 则 =( )A、 B、 C、 D、7. 不等式 的解集是()A、 B、 C、 D、8. 不等式组 表示的平面区域是()A、
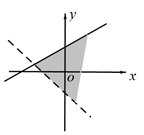 B、
B、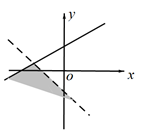 C、
C、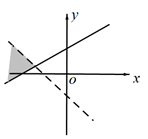 D、
D、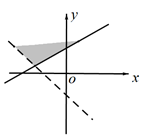 9. 若 对任意 恒成立,则 的取值范围是()A、 B、 C、 D、10. 已知 ,下列选项中正确的是( )A、 B、 C、 D、
9. 若 对任意 恒成立,则 的取值范围是()A、 B、 C、 D、10. 已知 ,下列选项中正确的是( )A、 B、 C、 D、二、多选题
-
11. 对任意x,y, ,则( )A、 B、 C、 D、
三、填空题
-
12. 已知 中,点D在边BC上, .当 取得最小值时, .13. 若曲线 有两条过坐标原点的切线,则a的取值范围是.14. 不等式 的解集为
四、解答题
-
15. 已知a,b,c都是正数,且 ,证明:(1)、 ;(2)、 .16. 记 的内角A,B,C的对边分别为a,b,c,已知(1)、若 求B;(2)、求 的最小值.17. 如图,矩形ABCD区域内,D处有一棵古树,为保护古树,以D为圆心,DA为半径划定圆D作为保护区域,已知 m, m,点E为AB上的动点,点F为CD上的动点,满足EF与圆D相切.
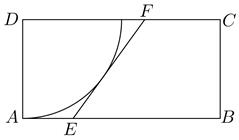 (1)、若∠ADE ,求EF的长;(2)、当点E在AB的什么位置时,梯形FEBC的面积有最大值,最大面积为多少?
(1)、若∠ADE ,求EF的长;(2)、当点E在AB的什么位置时,梯形FEBC的面积有最大值,最大面积为多少?(长度精确到0.1m,面积精确到0.01m²)
18. 已知函数 ,甲变化: ;乙变化: , .(1)、若 , , 经甲变化得到 ,求方程 的解;(2)、若 , 经乙变化得到 ,求不等式 的解集;(3)、若 在 上单调递增,将 先进行甲变化得到 ,再将 进行乙变化得到 ;将 先进行乙变化得到 ,再将 进行甲变化得到 ,若对任意 ,总存在 成立,求证: 在R上单调递增.
-