初中数学暑假作业（人教版：八年级升九年级）：03平行四边形
试卷更新日期：2022-07-07 类型：同步测试
一、单选题
-
1. 如图，直线AB∥CD，P是AB上的动点，当点P的位置变化时，三角形PCD的面积将（ ）
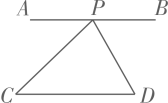A、变大 B、变小 C、不变 D、无法确定2. 如图，在平行四边形ABCD中， ， ， 以点C为圆心，适当长为半径画弧，交BC于点P，交CD于点Q，再分别以点P，Q为圆心，大于的长为半径画弧，两弧相交于点N，射线CN交BA的延长线于点E，则AE的长是（ ）
A、1 B、2 C、3 D、43. 如图，在中，分别取AB、AC的中点D、E，连接DE，过点A作 ， 垂足为F，将分割后拼接成矩形BCHG，若 ， ， 则的面积是（ ）
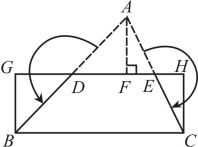A、8 B、10 C、14 D、164. 如图，在Rt△ABC中， ， ， ． 将△ABC沿BC方向向右平移得到△DEF，若四边形ACFD的周长为10，则△ABC平移的距离为（ ）
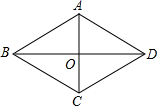
A、1 B、2 C、 D、45. 如果矩形的一个内角的平分线把矩形的一边分成了3cm和5cm的两部分，则矩形的较短边长为（ ）A、3 cm B、5 cm C、3 cm或5 cm D、2 cm或5 cm6. 如图所示，矩形ABCD的两条对角线AC，BD的一个夹角∠AOB=60°，AC=12cm，则这个矩形的一条较短边为（ ）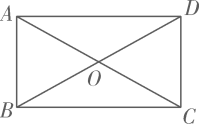
A、12cm B、8cm C、6cm D、5cm7. 如图，菱形ABCD的对角线AC，BD交于点O，∠BAC=52°，则∠CDO的度数是（ ）
A、52° B、44° C、40° D、38°8. 已知四边形ABCD是平行四边形，下列说法：①当 时，它是矩形；② 时，它是菱形；③当 时，它是菱形；④当 时，它是正方形.其中正确的有（ ）A、①② B、②④ C、③④ D、②9. 如图，正方形硬纸片ABCD的边长是4，E.F分别是AB，BC的中点，若沿左下图中的虚线剪开，拼成如下图所示的一座“小别墅”，则图中阴影部分的面积是（ ）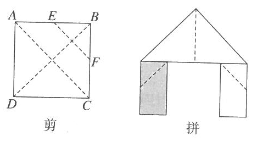
A、2 B、4 C、8 D、1010. 如图是由5个全等的边长为1的正方形拼成的图形，现有两种不同的方式将它沿着虚线剪开，如图甲将它分成三块，如图乙将它分成四块，各自要拼一个面积是5的大正方形，则（ ）
A、甲、乙都可以 B、甲可以，乙不可以 C、甲不可以，乙可以 D、甲、乙都不可以二、填空题
-
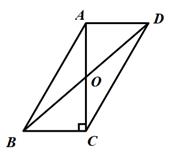
11. 如图，在平行四边形ABCD中，对角线AC，BD交于点O，AC⊥BC，若AB＝8，AD＝4，则BD的长为 ．
12. 如图，EF是△ABC的中位线，O是EF上一点，且满足OE=2OF.则△ABC的面积与△AOC的面积之比为 ．
13. 如图，在△ABC中，BC=8，AC=6，AB=10，它们的中点分别是D、E、F，则CF=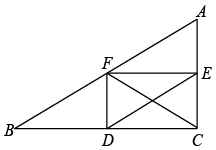
14. 如图，矩形中，对角线的垂直平分线分别交 ， 于点E，F，若 ， ， 则的长为.
15. 如图，点E在正方形ABCD中，△BEC是等边三角形，则∠EAD＝°．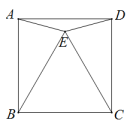
三、解答题
-
16. 如图，在▱ABCD中，点E，F分别在边AB，CD上，BE＝DF，EF与对角线AC相交于点O．求证：OE＝OF．
17. 如图所示，在梯形ABCD中，DC∥AB，点E是BC的中点，连结AE并延长与DC的延长线相交于点F，连结BF，AC。求证：四边形ABFC是平行四边形。
18. 如图，在平行四边形 中， 分别是边 的中点；求证： ∥
19. 如图，在▱ABCD中，过点D作DE⊥AB于点E，点F在边CD上，DF＝BE.求证：四边形BEDF是矩形．
20. 如图，在 中，AF ， BH ， CH ， DF分别是 ， ， 与 的平分线，AF与BH交于点E ， CH与DF交于点G ．求证： ．
