初中数学暑假作业(人教版:八年级升九年级):02勾股定理
试卷更新日期:2022-07-07 类型:同步测试
一、单选题
-
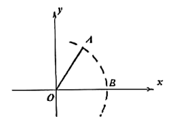
1. 如图,在平面直角坐标系中,已知点O(0,0),A(2,3),以点O为圆心,OA长为半径画弧,交x轴的正半轴于B点,则B点的横坐标介于( )
 A、3和4之间 B、4和5之间 C、5和6之间 D、6和7之间2. 如图,数轴上的点 表示的数是-2,点 表示的数是1, 于点 ,且 ,以点 为圆心, 为半径画弧交数轴于点 ,则点 表示的数为( )
A、3和4之间 B、4和5之间 C、5和6之间 D、6和7之间2. 如图,数轴上的点 表示的数是-2,点 表示的数是1, 于点 ,且 ,以点 为圆心, 为半径画弧交数轴于点 ,则点 表示的数为( ) A、 B、3 C、 D、3. 如图所示,小正方形的边长为1,连结小正方形的三个顶点可得△ABC,则AC边上的高是( )
A、 B、3 C、 D、3. 如图所示,小正方形的边长为1,连结小正方形的三个顶点可得△ABC,则AC边上的高是( ) A、 B、 C、 D、4. 若一个直角三角形的两条直角边长分别为 cm和 cm,那么此直角三角形的斜边长是( )A、3 cm B、3 cm C、9cm D、27 cm5. 如图,由两个全等菱形(菱形ABCD与菱形EFGH)组成的“四叶草”图案,其重叠部分是正八边形(阴影部分),点B,D在EG上,点F,H在AC上,若CF=2,则BD的长为( )
A、 B、 C、 D、4. 若一个直角三角形的两条直角边长分别为 cm和 cm,那么此直角三角形的斜边长是( )A、3 cm B、3 cm C、9cm D、27 cm5. 如图,由两个全等菱形(菱形ABCD与菱形EFGH)组成的“四叶草”图案,其重叠部分是正八边形(阴影部分),点B,D在EG上,点F,H在AC上,若CF=2,则BD的长为( ) A、4 B、2 C、2 D、26. 下列各组数中,以它们为边长的线段能构成直角三角形的是( )A、1,3,4 B、 C、5,12,13 D、7. 已知四个三角形分别满足下列条件:①一个内角等于另两个内角之和;②三个内角度数之比为3∶4∶5;③三边长分别为7,24,25;④三边长之比为5∶12∶13.其中直角三角形有( )A、1个 B、2个 C、3个 D、4个8. 如图,有一个绳索拉直的木马秋干,绳索AB的长度为5米,若将它往水平方向向前推进3米(即DE=3米),且绳索保持拉直的状态,则此时木马上升的高度为( )
A、4 B、2 C、2 D、26. 下列各组数中,以它们为边长的线段能构成直角三角形的是( )A、1,3,4 B、 C、5,12,13 D、7. 已知四个三角形分别满足下列条件:①一个内角等于另两个内角之和;②三个内角度数之比为3∶4∶5;③三边长分别为7,24,25;④三边长之比为5∶12∶13.其中直角三角形有( )A、1个 B、2个 C、3个 D、4个8. 如图,有一个绳索拉直的木马秋干,绳索AB的长度为5米,若将它往水平方向向前推进3米(即DE=3米),且绳索保持拉直的状态,则此时木马上升的高度为( ) A、1米 B、 米 C、2米 D、4米9. 在 中,若 ,则( )A、 B、 C、 D、不能确定10. 如图,“今有竹高两丈五尺,末折抵地,去本五尺,问折者高几何?”意思是:一根竹子,原来高两丈五尺(一丈为十尺),虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子根部五尺远,则折断处离地面的高度为( )
A、1米 B、 米 C、2米 D、4米9. 在 中,若 ,则( )A、 B、 C、 D、不能确定10. 如图,“今有竹高两丈五尺,末折抵地,去本五尺,问折者高几何?”意思是:一根竹子,原来高两丈五尺(一丈为十尺),虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子根部五尺远,则折断处离地面的高度为( ) A、5尺 B、25尺 C、13尺 D、12尺
A、5尺 B、25尺 C、13尺 D、12尺二、填空题
-
11. 《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.《九章算术》中记载:“今有立木,系索其末,委地三尺.引索却行,去本八尺而索尽.问索长几何?”译文是:“今有一竖立着的木柱,在木柱的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有3尺(实际含义是:绳索比木柱长3尺).牵着绳索(绳索头与地面接触)退行,在距木柱根部8尺处时绳索用尽.问绳索长是多少?”设绳索长x尺,根据题意列方程为 .12. 已知P是直角坐标系内一点,若点P的坐标为( , ),则它到原点的距离是13. 如图,在 中, , , ,则 的面积为.
 14. 如图,一木杆在离地面1.5m处折断,木杆顶端落在离木杆底端 处,则木杆折断之前的高(m).
14. 如图,一木杆在离地面1.5m处折断,木杆顶端落在离木杆底端 处,则木杆折断之前的高(m). 15. 如图,在 中, ,在边 上截取 ,连接 ,过点 作 于点 .已知 , ,如果 是边 的中点,连接 ,那么 的长是 .
15. 如图,在 中, ,在边 上截取 ,连接 ,过点 作 于点 .已知 , ,如果 是边 的中点,连接 ,那么 的长是 .
三、解答题
-
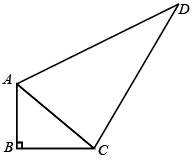
16. 已知CD是的边AB上的高,若 , , , 求AB长.17. 如图,已知∠B=∠ADC=90°,DC=7,AB=20,BC=15,求AD的长.
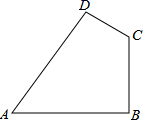 18. 如图,四边形ABCD中, , , , ,求四边形ABCD的面积.
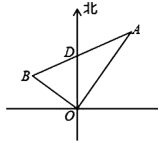
18. 如图,四边形ABCD中, , , , ,求四边形ABCD的面积. 19. 某快递公司为了给客户提供“安全、快速”的优质服务,购置了一台无人机往返A,B,C三地运输货物,如图所示,幸福小区C位于快递站点B的北偏东35°方向,沁苑小区A位于快递站点B的南偏东55°方向,无人机以1千米/分钟的速度配送快递时,从B到C需飞行8分钟,从B到A需飞行15分钟.请求出无人机从幸福小区C与沁苑小区A之间所需要的时间。
19. 某快递公司为了给客户提供“安全、快速”的优质服务,购置了一台无人机往返A,B,C三地运输货物,如图所示,幸福小区C位于快递站点B的北偏东35°方向,沁苑小区A位于快递站点B的南偏东55°方向,无人机以1千米/分钟的速度配送快递时,从B到C需飞行8分钟,从B到A需飞行15分钟.请求出无人机从幸福小区C与沁苑小区A之间所需要的时间。 20. 如图,在△ABC中,CD是高,AD=4,CD=2, BD=1,求证:∠ACB=90°.
20. 如图,在△ABC中,CD是高,AD=4,CD=2, BD=1,求证:∠ACB=90°. 21. 如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子 的长为17米,此人以1米每秒的速度收绳,7秒后船移动到点 的位置,问船向岸边移动了多少米?(假设绳子是直的)
21. 如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子 的长为17米,此人以1米每秒的速度收绳,7秒后船移动到点 的位置,问船向岸边移动了多少米?(假设绳子是直的)