2022年浙教版数学九年级上学期第1章二次函数单元测试

试卷更新日期：2022-07-07 类型：单元试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. 如图，若抛物线 $y = a x^{2} - 2 x + a^{2} - 1$ 经过原点，则抛物线的解析式为（）

A、 $y = - x^{2} - 2 x$ B、 $y = x^{2} - 2 x$ C、 $y = - x^{2} - 2 x + 1$ D、 $y = - x^{2} - 2 x$ 或 $y = x^{2} - 2 x$

查看试题解析
2. 抛物线y＝2x²＋1的对称轴是（）

A、直线 $x = \frac{1}{2}$ B、直线 $x = - \frac{1}{2}$ C、直线 $x = 2$ D、y轴

查看试题解析
3. 抛物线 $y = x^{2} - 4 x + 5$ 的顶点坐标是（）

A、 $(2 ， 1)$ B、 $(2 ， 5)$ C、 $(- 2 ， 1)$ D、 $(- 2 ， - 5)$

查看试题解析
4. 将二次函数 $y = {(x - 5)}^{2} - 24$ 的图象沿x轴向左平移2个单位长度，再沿y轴向上平移3个单位长度，得到的函数表达式是（）

A、 $y = {(x - 7)}^{2} - 27$ B、 $y = {(x - 7)}^{2} - 21$ C、 $y = {(x - 3)}^{2} - 27$ D、 $y = {(x - 3)}^{2} - 21$

查看试题解析
5. 如图，在平面直角坐标系中，将函数y＝x²－2x的图象先沿x轴翻折，再向上平移5个单位长度，得到的抛物线所对应的函数表达式是（）

A、 $y = - x^{2} + 2 x + 5$ B、 $y = - x^{2} + 2 x - 5$ C、 $y = - x^{2} - 2 x + 5$ D、 $y = - x^{2} - 2 x - 5$

查看试题解析
6. 函数y＝﹣x²﹣2x+m的图象上有两点A（1，y₁），B（2，y₂），则（）

A、y₁＜y₂ B、y₁＞y₂ C、y₁＝y₂ D、y₁、y₂的大小不确定

查看试题解析
7. 已知抛物线y＝ax²+bx+c（a，b，c为常数且a≠0）经过P₁（1，y₁），P₂（2，y₂），P₃（3，y₃），P₄（4，y₄）四点．若y₁＜y₂＜y₃ ，则下列说法中正确的是（）

A、若y₄＞y₃ ，则a＞0 B、对称轴不可能是直线x＝2.7 C、y₁＜y₄ D、3a+b＜0

查看试题解析
8. 已知抛物线 $y = x^{2} - 2 x - 3$ 经过A（-2， $y_{1}$ ），B（-1， $y_{2}$ ），C（1， $y_{3}$ ）三点，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是（）

A、 $y_{1} > y_{2} > y_{3}$ B、 $y_{2} > y_{1} > y_{3}$ C、 $y_{1} > y_{3} > y_{2}$ D、 $y_{3} > y_{2} > y_{1}$

查看试题解析
9. 二次函数y=x²﹣x+1的图象与x轴的交点个数是（）

A、0个 B、1个 C、2个 D、不能确定

查看试题解析
10. 一次函数 $y = b x + a (b \neq 0)$ 与二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 在同一平面直角坐标系中的图象可能是（）

A、 B、 C、 D、

查看试题解析

二、填空题（每题4分，共24分）

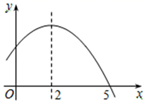
11. 已知抛物线y=2x²-x-1，与 $x$ 轴的一个交点为（m， 0），则代数式-4m²+2m+2022的值为.

查看试题解析
12. 如图是二次函数y=-x²+bx+c的部分图象，若 $y \geq 0$ ，则x的取值范围是.

查看试题解析
13. 已知点P（x₀ ， m），Q（1，n）在二次函数y＝（x+a）（x﹣a﹣1）（a≠0）的图象上，且m＜n下列结论：①该二次函数与x轴交于点（﹣a，0）和（a+1，0）；②该二次函数的对称轴是x＝ $\frac{1}{2}$ ； ③该二次函数的最小值是（a+2）²； ④0＜x₀＜1．其中正确的是．（填写序号）

查看试题解析
14. 将抛物线 $y = x^{2}$ 向上平移3个单位，所得图象的函数表达式是。

查看试题解析
15. 抛物线 $y = - \frac{1}{2} {(x - 2)}^{2} + 5$ 的顶点坐标是.

查看试题解析
16. 二次函数y＝ax²+bx+c（a≠0）的图象如图所示，则关于x的方程ax²+bx+c＝0（a≠0）的解为．

查看试题解析

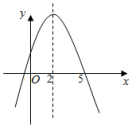
三、解答题（共8题，共66分）

17. 一个二次函数的图象经过 $(- 1 ， 0)$ ， $(0 ， 6)$ ， $(3 ， 0)$ 三点．求：这个二次函数的解析式．

查看试题解析
18. 已知二次函数y＝x²﹣4x+c（c是常数）的图象与x轴只有一个交点，求c的值及这个交点的坐标．

查看试题解析
19. 已知二次函数y＝x²﹣mx+2m﹣4
证明：无论m取任何实数时，该函数图象与x轴总有交点

查看试题解析
20. 某公司今年国庆期间在网络平台上进行直播销售猕猴桃，已知猕猴桃的成本价格为8元／kg，经销售发现：每日销售量y（kg）与销售单价x（元／kg）满足一次函数关系，下表记录的是有关数据，销售单价不低于成本价且不高于24元／kg．设公司销售猕猴桃的日获利为w（元）.

x（元／kg）

9

10

11

y(kg)

2100

2000

1900

(1)、请求出日销售量y与销售单价x之间的函数关系式；

(2)、当销售单价定为多少时，销售这种猕猴桃日获利w最大？最大利润为多少元？

查看试题解析
21. 如图，二次函数y＝x2＋bx＋c的图象与x轴交于A，B两点，与y轴交于点C，且关于直线x＝1对称，点A的坐标为（-1，0）．

(1)、求二次函数的表达式；

(2)、当y＜0时，写出x的取值范围；

(3)、当a≤x≤a＋1时，二次函数y＝x²＋bx＋c的最小值为2a，求a的值．

查看试题解析
22. 如图1，在平面直角坐标系 $x O y$ 中，抛物线 $y = a x^{2} + b x$ 经过点 $(- 2 ， 5)$ ，且与直线 $y = - \frac{1}{2} x$ 在第二象限交于点A，过点A作 $A B ⊥ x$ 轴，垂足为点 $B (- 4 ， 0)$ .若P是直线 $O A$ 上方该抛物线上的一个动点，过点P作 $P C ⊥ x$ 轴于点C，交 $O A$ 于点D，连接 $O P$ ， $P A$ .

(1)、求抛物线的解析式；

(2)、求 $△ A O P$ 的面积S的最大值；

(3)、连接 $P B$ 交 $O A$ 于点E，如图2，线段 $P B$ 与 $A D$ 能否互相平分？若能，请求出点E的坐标；若不能，请说明理由.

查看试题解析
23. 如图，在平面直角坐标系中，抛物线 $y = a x^{2} + b x - 3$ 过点 $A (- 3 ， 0)$ ， $B (1 ， 0)$ ，与y轴交于点C，连接BC，点N是第一象限抛物线上一点，连接NA，交y轴于点E， $∠ N A B = ∠ B C O$ ．

(1)、求抛物线的解析式；

(2)、求线段AN的长；

(3)、若点M在第三象限抛物线上，连接MN， $∠ A N M = 45 °$ ，则这时点M的坐标为（直接写出结果）．

查看试题解析
24. 在平面直角坐标系中，若直线 $l ： y = k x + b (k \neq 0)$ 与函数G的图象有且只有一个交点P.则称该直线l是函数G关于点P的“联络直线”，点P称为“联络点”.

(1)、直线 $y = - x + 1$ 是函数 $y = \frac{1}{x}$ 的“联络直线”吗？请说明理由；

(2)、已知函数 $y = \frac{12}{x}$ ，求该函数关于“联络点” $(3 ， 4)$ 的“联络直线”的解析式；

(3)、若关于x的函数 $y = a x^{2} - 2 a x - 3 a (a > 0)$ 图象与x轴交于A、B两点，与y轴交于点C，点P是y轴上一点，分别过点P作函数 $y = a x^{2} - 2 a x - 3 a$ 关于点M，N的“联络直线”PM、PN.若直线 $y = k x - 1$ 恰好经过M、N两点，请用含a的式子表示线段PC的长.

查看试题解析

x（元／kg）	9	10	11
y(kg)	2100	2000	1900

2022年浙教版数学九年级上学期第1章 二次函数 单元测试

一、单选题（每题3分，共30分）

二、填空题（每题4分，共24分）

三、解答题（共8题，共66分）

2022年浙教版数学九年级上学期第1章二次函数单元测试