河北省保定市2021-2022学年高一下学期数学期末考试试卷
试卷更新日期:2022-07-07 类型:期末考试
一、单选题
-
1. 若 , 则( )A、 B、 C、5-i D、2. 某社区卫生室为了了解该社区居民的身体健康状况,对该社区2000名男性居民和1600名女性居民按性别采用等比例分层随机抽样的方法进行抽样调查,抽取了一个容量为180的样本,则应从女性居民中抽取的人数为( )A、60 B、80 C、90 D、1003. 已知非零向量 , 且与共线,则( )A、-3 B、2 C、3 D、0或34. 如图,已知通过斜二测画法得到的直观图是面积为2的等腰直角三角形,则为( )
 A、面积为的等腰三角形 B、面积为的等腰三角形 C、面积为的直角三角形 D、面积为的直角三角形5. 一艘船航行到点处时,测得灯塔与其相距30海里,如图所示.随后该船以20海里/小时的速度,沿直线向东南方向航行1小时后到达点 , 测得灯塔在其北偏东方向,则( )
A、面积为的等腰三角形 B、面积为的等腰三角形 C、面积为的直角三角形 D、面积为的直角三角形5. 一艘船航行到点处时,测得灯塔与其相距30海里,如图所示.随后该船以20海里/小时的速度,沿直线向东南方向航行1小时后到达点 , 测得灯塔在其北偏东方向,则( )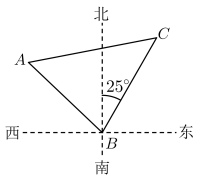 A、 B、 C、 D、6. 已知 , 则( )A、 B、 C、 D、7. 某圆锥的母线长为4,高为3,则该圆锥外接球的表面积为( )A、16π B、 C、24π D、8. 已知向量满足 , 则的最大值为( )A、 B、 C、 D、
A、 B、 C、 D、6. 已知 , 则( )A、 B、 C、 D、7. 某圆锥的母线长为4,高为3,则该圆锥外接球的表面积为( )A、16π B、 C、24π D、8. 已知向量满足 , 则的最大值为( )A、 B、 C、 D、二、多选题
-
9. 在正方体中,分别为的中点,则( )A、与异面 B、平面平面 C、平面平面 D、与所成角的正切值为10. 为了解某地高一学生的期末考试语文成绩,研究人员随机抽取了100名学生对其进行调查,根据所得数据制成如图所示的频率分布直方图(各组区间均为左闭右开),已知不低于90分为及格,则( )
 A、 B、这100名学生期末考试语文成绩的及格率为55% C、 D、这100名学生期末考试语文成绩的及格率为60%11. 中国象棋是中国发明的一种古老的棋类游戏,大约有两千年的历史,是中华文明非物质文化的经典产物.如图,棋盘由边长为1的正方形方格组成,已知“帅”“炮”“马”“兵”分别位于四点,“马”每步只能走“日”字,图中的“马”走动一步到达点 , 则的值可能为( )
A、 B、这100名学生期末考试语文成绩的及格率为55% C、 D、这100名学生期末考试语文成绩的及格率为60%11. 中国象棋是中国发明的一种古老的棋类游戏,大约有两千年的历史,是中华文明非物质文化的经典产物.如图,棋盘由边长为1的正方形方格组成,已知“帅”“炮”“马”“兵”分别位于四点,“马”每步只能走“日”字,图中的“马”走动一步到达点 , 则的值可能为( ) A、-10 B、-12 C、-11 D、-1412. 已知函数在上单调,且 , 则( )A、函数的图象关于原点对称 B、的图象向左平移个单位长度后可能得到的图象 C、的值不可能是整数 D、在上仅有两个零点
A、-10 B、-12 C、-11 D、-1412. 已知函数在上单调,且 , 则( )A、函数的图象关于原点对称 B、的图象向左平移个单位长度后可能得到的图象 C、的值不可能是整数 D、在上仅有两个零点三、填空题
-
13. 河北省九大高峰按照海拔(单位:米)排名依次为小五台山(2882)、驼梁山(2281)、雾灵山(2118)、长城岭(2100)、白石山(2096)、野三坡(1983)、祖山(1428)、天桂山(1270)、狼牙山(1105),则这九大高峰的海拔数据的第70百分位数为.14. 某圆台的上、下底面圆的半径分别为 , 且该圆台的体积为 , 则该圆台的高为.15. 已知函数的图象关于直线对称,且在上单调,则的最大值为.16. 如图,在三棱锥中,平面米,米,与底面所成角的正切值为2.已知蚂蚁从点出发,沿着侧面走到上的一点,再沿着侧面继续走到棱上,则这只蚂蚁从点出发到达棱的最短路程为米,这只蚂蚁的最短路线与的交点到底面的距离为米.

四、解答题
-
17. 已知复数.(1)、求;(2)、若 , 且为纯虚数,求在复平面内对应的点的坐标.18. 在四边形中,.(1)、若 , 证明:四边形为菱形.(2)、已知为的中点,设 , 试用表示.19. 如图,在正方体中,分别为的中点.
 (1)、证明:平面.(2)、若 , 求四棱锥的体积.20. 在中,内角的对边分别为.已知.(1)、求;(2)、若的面积为 , 且为的中点,求线段的长.21. 已知甲工厂生产一种内径为的零件,为了了解零件的生产质量,从该厂的2000件零件中抽出100件,测得其内径尺寸如下(单位:): , , , , , , .注:表示有件尺寸为的零件.(1)、求这100件零件内径尺寸的平均数;(2)、设这100件零件内径尺寸的方差为 , 试估计该厂2000件零件中其内径尺寸(单位:在内的件数;(3)、若乙工厂也生产同种零件,为了了解零件的生产质量,从该厂的2000件零件中抽出100件,测得其内径(单位:)的方差为 , 试比较甲、乙两工厂抽检的100件零件内径尺寸的稳定性.22. 如图,在四棱锥中,平面 , 底面是直角梯形,为的中点.
(1)、证明:平面.(2)、若 , 求四棱锥的体积.20. 在中,内角的对边分别为.已知.(1)、求;(2)、若的面积为 , 且为的中点,求线段的长.21. 已知甲工厂生产一种内径为的零件,为了了解零件的生产质量,从该厂的2000件零件中抽出100件,测得其内径尺寸如下(单位:): , , , , , , .注:表示有件尺寸为的零件.(1)、求这100件零件内径尺寸的平均数;(2)、设这100件零件内径尺寸的方差为 , 试估计该厂2000件零件中其内径尺寸(单位:在内的件数;(3)、若乙工厂也生产同种零件,为了了解零件的生产质量,从该厂的2000件零件中抽出100件,测得其内径(单位:)的方差为 , 试比较甲、乙两工厂抽检的100件零件内径尺寸的稳定性.22. 如图,在四棱锥中,平面 , 底面是直角梯形,为的中点. (1)、证明:平面.(2)、若二面角的正切值为 , 求二面角的正弦值.
(1)、证明:平面.(2)、若二面角的正切值为 , 求二面角的正弦值.