山东省淄博市桓台县2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-07-07 类型:期末考试
一、单选题
-
1. 下列多项式不能用公式法进行因式分解的是( )A、 B、 C、 D、2. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 要使分式有意义,则x的取值应满足( )A、 B、 C、 D、4. 如图,在中,若 , 则的度数为( )
3. 要使分式有意义,则x的取值应满足( )A、 B、 C、 D、4. 如图,在中,若 , 则的度数为( ) A、 B、 C、 D、5. 今年收获一批成熟的果子,选取了5棵果树,采摘后分别称重,每棵果树果子总质量(单位:kg)分别为:90,100,120,110,90.这五个数据的众数和中位数分别是( )A、90,120 B、90,110 C、90,100 D、100,1006. ABC的顶点分别位于格点(网格线的交点)上,建立如图所示的平面直角坐标系,将ABC先沿x轴方向向右平移3个单位长度,再沿y轴方向向下平移2个单位长度,得到 , 则点A的对应点的坐标是( )
A、 B、 C、 D、5. 今年收获一批成熟的果子,选取了5棵果树,采摘后分别称重,每棵果树果子总质量(单位:kg)分别为:90,100,120,110,90.这五个数据的众数和中位数分别是( )A、90,120 B、90,110 C、90,100 D、100,1006. ABC的顶点分别位于格点(网格线的交点)上,建立如图所示的平面直角坐标系,将ABC先沿x轴方向向右平移3个单位长度,再沿y轴方向向下平移2个单位长度,得到 , 则点A的对应点的坐标是( ) A、(0,2) B、(﹣6,6) C、(0,6) D、(﹣6,2)7. 如图,在等腰直角中, , D为内一点,将线段绕点C逆时针旋转90°后得到 , 连接 , 若 , 则是( )
A、(0,2) B、(﹣6,6) C、(0,6) D、(﹣6,2)7. 如图,在等腰直角中, , D为内一点,将线段绕点C逆时针旋转90°后得到 , 连接 , 若 , 则是( ) A、75° B、78° C、80° D、92°8. 如图,将三角形纸片沿折叠,当点A落在四边形的外部时,测量得 , , 则的度数为( )
A、75° B、78° C、80° D、92°8. 如图,将三角形纸片沿折叠,当点A落在四边形的外部时,测量得 , , 则的度数为( ) A、 B、 C、 D、9. 如图,在中, , 点D,E,F分别是三边的中点,且 , 则的长度是( )
A、 B、 C、 D、9. 如图,在中, , 点D,E,F分别是三边的中点,且 , 则的长度是( ) A、 B、 C、 D、10. 如图,桐桐从A点出发,前进3m到点B处后向右转20°,再前进3m到点C处后又向右转20°,…,这样一直走下去,她第一次回到出发点A时,一共走了( )
A、 B、 C、 D、10. 如图,桐桐从A点出发,前进3m到点B处后向右转20°,再前进3m到点C处后又向右转20°,…,这样一直走下去,她第一次回到出发点A时,一共走了( ) A、100m B、90m C、54m D、60m11. 如图,在中, , 将绕点A按顺时针方向旋转得到 . 若点恰好落在边上,且 , 则的度数为( )
A、100m B、90m C、54m D、60m11. 如图,在中, , 将绕点A按顺时针方向旋转得到 . 若点恰好落在边上,且 , 则的度数为( ) A、 B、 C、 D、12. 如图,在中,以A为圆心,长为半径画弧,交于F点,分别以点F,B为圆心,大于为半径画弧,两弧交于点G,作射线交于点E,若 , , 则的长为( )
A、 B、 C、 D、12. 如图,在中,以A为圆心,长为半径画弧,交于F点,分别以点F,B为圆心,大于为半径画弧,两弧交于点G,作射线交于点E,若 , , 则的长为( ) A、4 B、6 C、7 D、8
A、4 B、6 C、7 D、8二、填空题
-
13. 一组数据﹣1、2、3、4的极差是 .14. 已知,实数a满足 , 则 .15. 若点和点关于原点对称,则的值为 .16. 如图,将直角三角形沿方向平移后,得到直角三角形 . 已知 , 则阴影部分的面积为 .
 17. 如图,平行四边形ABCD中,对角线AC、BD相交于点O,若AB=2,BC=3, , 则图中阴影部分的面积是 .
17. 如图,平行四边形ABCD中,对角线AC、BD相交于点O,若AB=2,BC=3, , 则图中阴影部分的面积是 .
三、解答题
-
18. 绿水青山就是金山银山,为了改善生态环境,某村计划在荒坡上种树960棵.防止雨季到来,影响工期,实际每天种树的棵数是原计划的倍,结果提前4天完成任务.原计划每天种树多少棵?19. 已知的边长如图所示,求的周长.
 20. 已知,如图在中,对角线和相交于点O,点E,F分别在 , 上,且 , 连接 , .
20. 已知,如图在中,对角线和相交于点O,点E,F分别在 , 上,且 , 连接 , .
 (1)、如图1,求证:;(2)、如图2,延长交于点G,延长交于点H.求证: .21. 如图,正方形网格中,每个小正方形的边长都是单位1,的位置如图.
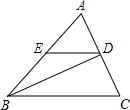
(1)、如图1,求证:;(2)、如图2,延长交于点G,延长交于点H.求证: .21. 如图,正方形网格中,每个小正方形的边长都是单位1,的位置如图. (1)、画出将向右平移2个单位得到的;(2)、画出绕点O顺时针旋转后得到的;(3)、写出的坐标;写出的坐标 .22. 如图,在中,D,E分别是边 , 的中点,连接 , . 若平分 , 求证: .
(1)、画出将向右平移2个单位得到的;(2)、画出绕点O顺时针旋转后得到的;(3)、写出的坐标;写出的坐标 .22. 如图,在中,D,E分别是边 , 的中点,连接 , . 若平分 , 求证: .