山东省临沂市河东区2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-07-07 类型：期末考试

进入出卷网下载

一、单选题

1. 如图的面积关系，可以得到的恒等式是（　　）

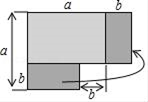A、m（a+b+c）＝ma+mb+mc B、（a+b）（a﹣b）＝a²﹣b² C、（a﹣b）²＝a²﹣2ab+b² D、（a+b）²＝a²+2ab+b²

查看试题解析
2. 如图，已知D为 $△ A B C$ 边 $A B$ 的中点，E在 $A C$ 上，将 $△ A B C$ 沿着 $D E$ 折叠，使A点落在 $B C$ 上的F处．若 $∠ B = 70 °$ ，则 $∠ B D F$ 等于（）

A、65 $°$ B、 $50 °$ C、 $40 °$ D、 $37.5 °$

查看试题解析
3. 已知点P(a，3)，Q(−2，b)关于y轴对称，则 $\frac{2 a + b}{a - 2 b} =$ （）

A、 $- 2$ B、 $2$ C、 $- \frac{7}{4}$ D、 $\frac{7}{4}$

查看试题解析
4. 到△ABC的三个顶点距离相等的点是 ( )

A、三条中线的交点 B、三条角平分线的交点 C、三条高线的交点 D、三条边的垂直平分线的交点

查看试题解析
5. 对于非零实数 $a 、 b$ ，规定 $a \oplus b = \frac{1}{b} - \frac{1}{a}$ ，若 $2 \oplus (2 x - 1) = 1$ ，则 $x$ 的值为（）

A、 $\frac{5}{6}$ B、 $\frac{5}{4}$ C、 $\frac{3}{2}$ D、 $- \frac{1}{6}$

查看试题解析
6. 已知关于x的方程 $\frac{x}{x - 5} = 3 - \frac{a}{x - 5}$ 有增根，则a的值为（　　）

A、4 B、5 C、6 D、﹣5

查看试题解析
7. 如图，在 $3 \times 3$ 的正方形网格中，格线的交点称为格点，以格点为顶点的三角形称为格点三角形，图中的 $△ A B C$ 为格点三角形，在图中与 $△ A B C$ 成轴对称的格点三角形可以画出（）

A、6个 B、5个 C、4个 D、3个

查看试题解析
8. 已知 $a^{4} + \frac{1}{a^{4}} = 14$ ，则 $a^{2} + \frac{1}{a^{2}}$ 等于（）

A、3 B、 $\pm 4$ C、 $- 4$ D、4

查看试题解析
9. 如图，过边长为4的等边 $△ A B C$ 的边AB上一点P，作PE⊥AC于E，Q为BC延长线上一点，当PA=CQ时，连PQ交AC边于D，则DE的长为（）

A、 $\frac{9}{5}$ B、2 C、 $\frac{11}{5}$ D、 $\frac{12}{5}$

查看试题解析
10. 已知 $\frac{1}{4} m^{2} + \frac{1}{4} n^{2} = n - m - 2$ ，则 $\frac{m}{2} - \frac{n}{2}$ 的值等于（）

A、1 B、﹣1 C、-2 D、 $\frac{1}{4}$

查看试题解析
11. 已知对任意实数x，式子 $\frac{x - 2}{x^{2} - 4 x + m}$ 都有意义，则实数m的取值范围是（）

A、 $m > 4$ B、 $m < 4$ C、 $m ⩾ 4$ D、 $m ⩽ 4$

查看试题解析
12. 已知实数a，b满足 $\frac{1}{a^{2}} + \frac{1}{b^{2}} = \frac{4}{a^{2} + b^{2}}$ ，则 ${(\frac{b}{a})}^{2022} - {(\frac{b}{a})}^{2021}$ 的值为（）

A、0或2 B、0或-2 C、-2 D、0

查看试题解析
13. 如图，在Rt△ABC中，∠ACB＝90°，∠CAB=36°，以C为原点，C所在直线为y轴，BC所在直线为x轴建立平面直角坐标系，在坐标轴上取一点M使△MAB 为等腰三角形，符合条件的 M 点有（）

A、6个 B、7个 C、8个 D、9个

查看试题解析
14. 如图， $A D$ 为 $∠ C A F$ 的角平分线， $B D = C D$ ，过 $D$ 作 $D E ⊥ A C$ 于 $E$ ， $D F ⊥ A B$ 交 $B A$ 的延长线于 $F$ ，则下列结论：① $Δ C D E ≅ Δ B D F$ ；② $C E = A B + A E$ ；③ $∠ B D C = ∠ B A C$ ；④ $∠ D A F = ∠ C B D$ 其中正确结论的序号有（）

A、①②③④ B、②③④ C、①②③ D、①②④

查看试题解析

二、填空题

15. 在 $△ A B C$ 中，AB=a，BC=b， $△ A B C$ 的高AD与高CE的比是

查看试题解析
16. 已知等腰 $△ A B C$ 的一底角∠B=15°，且斜边AB＝6cm，则 $△ A B C$ 的面积为

查看试题解析
17. 如果x＋ $\frac{1}{x}$ ＝3，则 $\frac{x^{2}}{x^{4} + x^{2} + 1}$ 的值为．

查看试题解析
18. 若关于x的方程 $\frac{x + m}{x - 3}$ + $\frac{3 m}{3 - x}$ =3的解为正数，则m的取值范围是.

查看试题解析
19. 计算：15( $2^{4}$ +1)( $2^{8} + 1$ )( $2^{16} + 1$ )( $2^{32} + 1$ )=

查看试题解析

三、解答题

20. 计算：

(1)、 ${(- 1)}^{2022} + {(- \frac{1}{2})}^{- 2} - {(π - 3.14)}^{0} - \frac{1}{| - 2 |}$

(2)、 $\frac{x}{x - 3} - 1 = \frac{18}{(x + 3) (x - 3)}$ ．

查看试题解析
21.

(1)、已知直角 $△ A B C$ ， ∠C=90°，∠B=30°，求证：AB=2AC．

(2)、如图，AD是 $△ A B C$ 的角平分线，DE，DF分别是 $△$ ABD和 $△$ ACD的高，求证：AD垂直平分EF．

查看试题解析
22. 设 $M = \frac{a - 2}{1 + 2 a + a^{2}} \div (a - \frac{3 a}{a + 1})$ ．

(1)、化简M；

(2)、当a＝3时，记此时M的值为f(3)；当a＝4时，记此时M的值为f(4)；……．解关于x的不等式 $\frac{x - 2}{2} - \frac{7 - x}{4} \leq f (3) + f (4) + ⋯ + f (11)$ ．

查看试题解析
23. 如图，在△ABC中，D为BC的中点，过D点的直线GF交AC于点F，交AC的平行线BG于点G，DE⊥GF，并交AB于点E，连接EG，EF．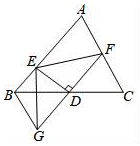

(1)、求证：BG＝CF．

(2)、请你猜想BE+CF与EF的大小关系，并说明理由．

查看试题解析
24. 受疫情影响，口罩需求量猛增，某商场用4000元购进一批口罩后，供不应求，商场用8800元购进第二批这种口罩，所购数量是第一批数量的2倍，但单价贵了0.2元．

(1)、求该商场购进的第二批口罩的单价；

(2)、商场销售这种口罩时，每只定价为3元，最后2000只按7.5折销售，很快售完，在这两笔生意中商场共获利多少元？

查看试题解析
25. 如图1，在 $△ A B C$ 中，∠A=120°，∠C=20°，BD平分∠ABC交AC于点D．

(1)、求证：BD=CD．

(2)、如图2，若∠BAC的角平分线AE交BC于点E，求证：AB+BE=AC．

(3)、如图3，若∠BAC的外角平分线AE交CB的延长线于点E，则（2）中的结论是否成立？若成立，给出证明，若不成立，写出正确的结论．

查看试题解析