山东省济南市天桥区2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-07-07 类型：期末考试

进入出卷网下载

一、单选题

1. 下列实数中，无理数是（）

A、0 B、5 C、-5 D、 $\sqrt{2}$

查看试题解析
2. 已知点A的坐标为（-4，3），则点A在（）

A、第一象限 B、第二象限 C、第三象服 D、第四象限

查看试题解析
3. 下列命题中，是真命题的是（）

A、对顶角相等 B、三角形的三个内角一定都是锐角 C、如果a²＝b² ，那么a＝b D、如果两直线平行，那么同旁内角相等

查看试题解析
4. 下列各点中，在直线y=-2x上的点是（）

A、（2，2） B、（－1，2） C、（2，－2） D、（－1，－1）

查看试题解析
5. 下列运算正确的是（）

A、 $\sqrt{3} \times \sqrt{5} = \sqrt{15}$ B、 $\sqrt[3]{16}$ ＝4 C、 $\sqrt{24} \div \sqrt{6} = 4$ D、 $\sqrt{4}$ ＝4

查看试题解析
6. 如图，直线a∥b，将含有45°的三角板ABC的直角顶点C放在直线b上，若∠1＝25°，则∠2的度数是（）

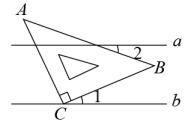A、10° B、15° C、25° D、20°

查看试题解析
7. 若 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ 是关于x 、y的二元一次方程ax－2y＝1的解，则a的值为（）

A、3 B、5 C、－3 D、－5

查看试题解析
8. 某校举行“喜迎中国共产党建党100周年”党史知识竞赛，下表是10名决赛选手的成绩．这10名决赛选手成绩的众数是（）
分数
100
95
90
85
人数
1
4
3
2

A、85 B、90 C、95 D、100

查看试题解析
9. 如图，直线y＝kx+b（b＞0）经过点（2，0），则关于x的不等式kx+b＞0的解集是（）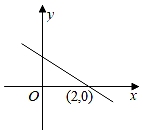

A、x＞2 B、x＜2 C、x≥2 D、x≤2

查看试题解析
10. 如图，等腰△ABC中，AB＝AC＝8，BC＝5，AB的垂直平分线DE交AB于点D，交AC于点E，则△BEC的周长为（）

A、12 B、8 C、15 D、13

查看试题解析
11. 已知点A的坐标为（1，2），直线AB∥x轴，且AB＝5，则点B的坐标为（）

A、（5，2）或（4，2） B、（6，2）或（-4，2） C、（6，2）或（－5，2） D、（1，7）或（1，－3）

查看试题解析
12. 对于一次函数y＝kx＋k－1，下列叙述正确的是（）

A、函数图象一定经过点（－1，－1） B、当k＜0时，y随x的增大而增大 C、当k＞0时，函数图象一定不经过第二象限 D、当0＜k＜1时，函数图象经过第一、二、三象限

查看试题解析

二、填空题

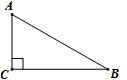
13. 4的算术平方根是．

查看试题解析
14. 不等式 $- 2 x > 10$ 的解集是．

查看试题解析
15. 甲、乙、丙三人进行射击测试，每人射击10次的平均成绩都是9.2环，方差分别是 $S_{甲}^{2} = 0.76$ ， $S_{乙}^{2} = 0.71$ ， $S_{丙}^{2} = 0.69$ ，则三人中成绩最稳定的是（填“甲”或“乙”或“丙”）．

查看试题解析
16. 如图，在 $R t △ A B C$ 中，∠C=90°，∠B=30°，AC=3，则AB= ．

查看试题解析
17. 如图所示的两架天平保持平衡，且每块巧克力的质量相等，每个果冻的质量也相等，则每块巧克力的质量为g．

查看试题解析
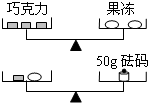18. 如图，在△ABC中，∠A＝60°，角平分线BD，CE交于点O，OF⊥AB于点F．下列结论：①∠EOB＝60°；②BF+CD＝BC；③AE+AD＝2AF；④S_四_边_形BEDC＝2S_△BOC+S_△EDO．其中正确结论是．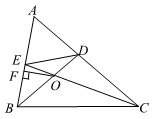

查看试题解析

三、解答题

19. 计算：

(1)、 $\sqrt{12} + \sqrt{27}$ ；

(2)、 $\frac{\sqrt{15} \times \sqrt{5}}{\sqrt{3}} - 2$ ．

查看试题解析
20.

(1)、解方程组 ${\begin{array}{l} x + y = 3 \\ x - y = 1 \end{array}$ ；

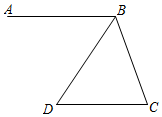
(2)、解不等式组 ${\begin{array}{l} x - 1 < 2 \\ 2 x + 1 \geq x - 1 \end{array}$ ．

查看试题解析
21. 如图，AB∥CD，连接BC，若BD平分∠ABC，∠D＝50°．求∠C的度数．

查看试题解析
22. 如图，已知Rt△ABC与Rt△DEF中，∠A＝∠D＝90°，点B、F、C、E在同一直线上，且AB＝DE，BF＝CE，求证：∠B＝∠E．

查看试题解析
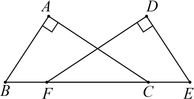23. 某学校举行“疫情防控”宣传活动，故购买A、B两种奖品以鼓励积极参与的学生．经市场调查发现，若购买A种6件、B种1件，共需100元；若购买A种5件、B种2件，共需88元．

(1)、A、B两种奖品每件各多少元?

(2)、学校决定现要购买A种奖品8件、B种奖品15件，那么总费用是多少元？

查看试题解析
24. 某养鸡场有2500只鸡准备对外出售，从中随机抽取了一部分鸡，根据它们的质量（单位：kg），绘制出如下的统计图①和图②．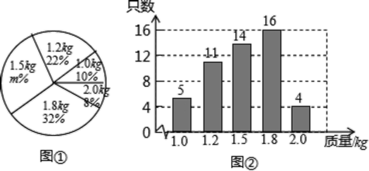
请根据相关信息，解答下列问题：

(1)、图①中m的值为；

(2)、直接写出统计的这组数据的众数和中位数；

(3)、根据样本数据，估计这2500只鸡中，质量为2.0kg的约有多少只?

查看试题解析
25. 如图甲、乙两人分别从同一公路上的A、B两地同时出发骑车前往C地，两人行驶的路程y（km）与甲行驶的时间x（h）之间的关系如图所示．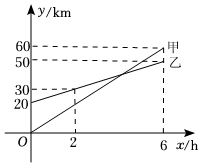
请根据图象所提供的信息解答下列问题：

(1)、A、B两地相距km，乙骑车的速度是km/h；

(2)、请分别求出甲、乙两人在0≤x≤6的时间段内y与x之间的函数关系式；

(3)、求何时甲、乙两人相距5千米．

查看试题解析
26. 在平面直角坐标系中，将一块等腰直角三角板ABC放在第一象限，斜靠在两条坐标轴上，∠ACB＝90°，且A（0，4），点C（2，0）．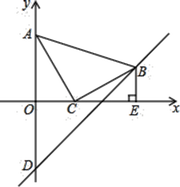

(1)、求直线AC的表达式和点B的坐标；

(2)、作BE⊥x轴于点E，一次函数y＝x＋b经过点B，交y轴于点D．
①求△ABD的面积；
②在直线AC上是否存在一点M，使得△MAE是以∠AEM为底角的等腰三角形，若存在，请直接写出点M的横坐标；若不存在，请说明理由．

查看试题解析
27. 已知△ABC和△ADE都是等腰三角形，且AB＝AC，AD＝AE，∠DAE＝∠BAC．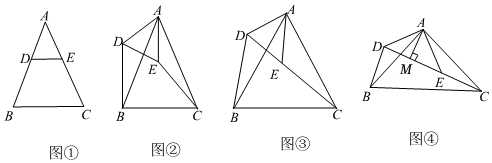

(1)、[初步感知]如图①，当点D、E分别落在边AB、AC上时，那么DBEC．（填＜、＞或＝）

(2)、[发现证明]如图②，将图①中的△ADE的绕点A旋转，当点D在△ABC外部，点E在△ABC内部时，求证：DB＝EC；

(3)、[深入研究]如图③，如果△ABC和△ADE都是等边三角形，且点C、E、D在同一条直线上，则∠CDB的度数为；线段CE、BD之间的数量关系为；

(4)、[拓展应用]如图④，如果△ABC和△ADE都是等腰直角三角形，∠BAC＝∠DAE＝90°，点C、D、E在同一直线上，作AM⊥DE，若AB＝ $\sqrt{6}$ ， BD＝ $\sqrt{3}$ ，求AM的长．

查看试题解析

分数	100	95	90	85
人数	1	4	3	2