山东省济南市市中区2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-07-07 类型:期末考试
一、单选题
-
1. 在实数 , 0,5,-π, , 中,无理数有( )个.A、4 B、3 C、2 D、12. 下列图形中,既是中心对称图形也是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列不能判定△ABC是直角三角形的是( )A、a2+b2-c2=0 B、a∶b∶c=3∶4∶5 C、∠A∶∠B∶∠C=3:4∶5 D、∠A+∠B=∠C4. 等腰三角形的两边分别为7和4,则它的周长是( )A、 B、 C、 D、5. 下列各点中,一定在第四象限的是( )A、(-3,-5) B、(3,5) C、(3,-5) D、(-3,5)6. 如图,在△ABC中,DM、EN分别垂直平分AB和AC,垂足为M,N.且分别交BC于点D,E.若∠DAE=20°,则∠BAC的度数为( )
3. 下列不能判定△ABC是直角三角形的是( )A、a2+b2-c2=0 B、a∶b∶c=3∶4∶5 C、∠A∶∠B∶∠C=3:4∶5 D、∠A+∠B=∠C4. 等腰三角形的两边分别为7和4,则它的周长是( )A、 B、 C、 D、5. 下列各点中,一定在第四象限的是( )A、(-3,-5) B、(3,5) C、(3,-5) D、(-3,5)6. 如图,在△ABC中,DM、EN分别垂直平分AB和AC,垂足为M,N.且分别交BC于点D,E.若∠DAE=20°,则∠BAC的度数为( )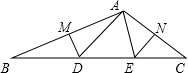 A、100° B、105° C、110° D、120°7. 已知方程组中,a,b互为相反数,则m的值是( )A、4 B、 C、0 D、88. 已知点(-3,y1)、(4,y2)在函数 y=2x+1 图像上,则y1与y2的大小关系是( )A、y1>y2 B、y1=y2 C、y1<y2 D、无法确定9. 如图,一次函数y=2x+1的图象与y=kx+b的图象相交于点A,则方程组的解是( )
A、100° B、105° C、110° D、120°7. 已知方程组中,a,b互为相反数,则m的值是( )A、4 B、 C、0 D、88. 已知点(-3,y1)、(4,y2)在函数 y=2x+1 图像上,则y1与y2的大小关系是( )A、y1>y2 B、y1=y2 C、y1<y2 D、无法确定9. 如图,一次函数y=2x+1的图象与y=kx+b的图象相交于点A,则方程组的解是( )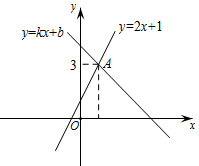 A、 B、 C、 D、10. 如图,在△ABC中,∠C=90°,AC=4cm,BC=3cm,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CD的长为( )
A、 B、 C、 D、10. 如图,在△ABC中,∠C=90°,AC=4cm,BC=3cm,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CD的长为( )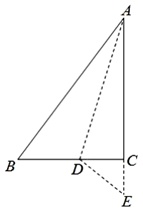 A、1cm B、cm C、cm D、2cm11. 如图,在大长方形ABCD中,放入六个相同的小长方形,则阴影部分的面积为( )
A、1cm B、cm C、cm D、2cm11. 如图,在大长方形ABCD中,放入六个相同的小长方形,则阴影部分的面积为( )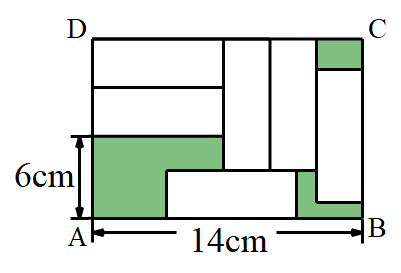 A、140 cm2 B、96cm2 C、44 cm2 D、16 cm212. 定义,图象与x轴有两个交点的函数y=叫做关于直线x=m的对称函数,它与x轴负半轴交点记为A,与x轴正半轴交点记为B例如:如图:直线l:x=1,关于直线l的对称函数y=与该直线l交于点C,当直线y=x与关于直线x=m的对称函数有两个交点时,则m的取值范围是( )
A、140 cm2 B、96cm2 C、44 cm2 D、16 cm212. 定义,图象与x轴有两个交点的函数y=叫做关于直线x=m的对称函数,它与x轴负半轴交点记为A,与x轴正半轴交点记为B例如:如图:直线l:x=1,关于直线l的对称函数y=与该直线l交于点C,当直线y=x与关于直线x=m的对称函数有两个交点时,则m的取值范围是( ) A、0≤m≤ B、-2<m≤ C、-2<m≤2 D、-4<m<0
A、0≤m≤ B、-2<m≤ C、-2<m≤2 D、-4<m<0二、填空题
-
13. 4的平方根是14. 数据3,3,4,4,6的方差等于。15. 如图,阴影部分是两个正方形,其它部分是两个直角三角形和一个正方形、若右边的直角三角形ABC中,AC=17,BC=15,则阴影部分的面积是 .
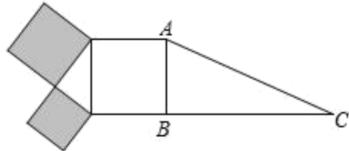 16. 如图,三角形中, , , , 将三角形沿方向平移2cm,连接 , 则四边形的周长是 .
16. 如图,三角形中, , , , 将三角形沿方向平移2cm,连接 , 则四边形的周长是 .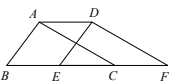 17. 如图,平面直角坐标系中,△ABC的顶点坐标分别是A(1,1),B(3,1),C(2,2),当直线y=x+b与△ABC有交点时,b的取值范围是 .
17. 如图,平面直角坐标系中,△ABC的顶点坐标分别是A(1,1),B(3,1),C(2,2),当直线y=x+b与△ABC有交点时,b的取值范围是 .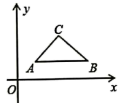 18. 如图,△ABC中,AC=DC=4,AD平分∠BAC,BD⊥AD于D,E为AC的中点,则图中两个阴影部分面积之差的最大值为 .
18. 如图,△ABC中,AC=DC=4,AD平分∠BAC,BD⊥AD于D,E为AC的中点,则图中两个阴影部分面积之差的最大值为 .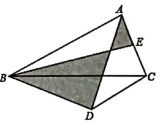
三、解答题
-
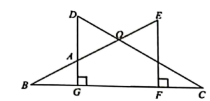
19. 计算:(1)、(2)、20. 解方程组: .21. 如图,CD=BE,DG⊥BC,EF⊥BC,垂足分别为G、F,且DG=EF,求证:OB=OC
 22. 如图,在平面直角坐标系中,Rt△ABC的三个顶点的坐标分别是A(-3,2),B(0,4),C(0,2).
22. 如图,在平面直角坐标系中,Rt△ABC的三个顶点的坐标分别是A(-3,2),B(0,4),C(0,2).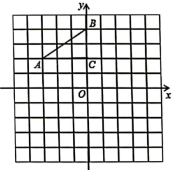
( 1 )将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;
( 2 )平移△ABC,若A的对应点的坐标为(0,-4),画出平移后对应的△A2B2C2;
( 3 )若将△A1B1C1绕某一点旋转可以得到△A2B2C2 , 请画出旋转中心P.
23. 为了解某校八年级学生的物理和生物实验操作情况,随机抽查了40名同学实验操作的得分(满分为10分).根据获取的样本数据,制作了下面的条形统计图和扇形统计图,请根据相关信息,解答下列问题. (1)、这40个样本数据平均数是 , 众数是 , 中位数是;(2)、扇形统计图中m的值为;扇形统计图中“6分”所对的圆心角的度数是;(3)、若该校八年级共有480名学生,估计该校物理和生物实验操作得满分的学生有多少人.24. 某商场计划购进A,B两种服装共100件,这两种服装的进价、售价如表所示:
(1)、这40个样本数据平均数是 , 众数是 , 中位数是;(2)、扇形统计图中m的值为;扇形统计图中“6分”所对的圆心角的度数是;(3)、若该校八年级共有480名学生,估计该校物理和生物实验操作得满分的学生有多少人.24. 某商场计划购进A,B两种服装共100件,这两种服装的进价、售价如表所示:价格
类型
进价(元/件)
售价(元/件)
A
30
45
B
50
70
(1)、若商场预计进货用3500元,则这两种服装各购进多少件?(2)、若商场规定A种服装进货不少于50件,应该怎样进货才能使商场销售完这批货时获利最多?此时利润为多少元?25. 甲、乙两车分别从BA两地同时出发,甲车匀速前往A地,乙车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地,设甲、乙两车离A地的路程为y(千米),乙车行驶的时间为x(时),y与x之间的函数图象如图所示.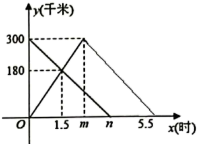 (1)、乙车从A地到达B地的速度是千米/时;(2)、乙车到达B地时甲车距A地的路程是千米;(3)、求乙车返回途中,甲、乙两车相距180千米时,乙车总共行驶的时间.26. 问题发现
(1)、乙车从A地到达B地的速度是千米/时;(2)、乙车到达B地时甲车距A地的路程是千米;(3)、求乙车返回途中,甲、乙两车相距180千米时,乙车总共行驶的时间.26. 问题发现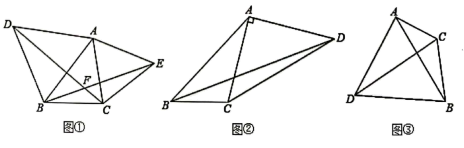 (1)、如图①,已知△ABC,以AB、AC为边向△ABC外分别作等边△ABD和等边△ACE,连接CD,BE.试猜想CD与BE的数量关系是;(2)、问题探究:如图②,四边形ABCD中,∠ABC=45°,∠CAD=90°,AC=AD,AB=2BC=6.求BD的长.(3)、问题解决:如图③,△ABC中,AC=2,BC=3,∠ACB是一个变化的角,以AB为边向△ABC外作等边△ABD,连接CD,求CD的长度最大值.27. 如图1,在平面直角坐标系xOy中,直线BC⊥AC,∠ABC=30°,点C(1,2),
(1)、如图①,已知△ABC,以AB、AC为边向△ABC外分别作等边△ABD和等边△ACE,连接CD,BE.试猜想CD与BE的数量关系是;(2)、问题探究:如图②,四边形ABCD中,∠ABC=45°,∠CAD=90°,AC=AD,AB=2BC=6.求BD的长.(3)、问题解决:如图③,△ABC中,AC=2,BC=3,∠ACB是一个变化的角,以AB为边向△ABC外作等边△ABD,连接CD,求CD的长度最大值.27. 如图1,在平面直角坐标系xOy中,直线BC⊥AC,∠ABC=30°,点C(1,2),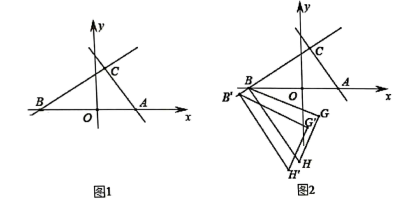 (1)、请直接写出点B的坐标;点A的坐标:;(2)、点P为直线BC上位于第一象限内一点,且△PAC的面积为16 , 求点P的坐标;(3)、如图2,将△ACB绕点B顺时针方向旋转60°,得到△BGH,使点A与点H重合,点C与点G重合,将△BGH沿直线BC平移,记平移中的△BGH为△B′G′H′,在平移过程中,设直线B′H′与x轴交于点M,是否存在这样的点M,使得△B′MG′为等腰三角形?若存在,求出此时点M的坐标;若不存在,说明理由.
(1)、请直接写出点B的坐标;点A的坐标:;(2)、点P为直线BC上位于第一象限内一点,且△PAC的面积为16 , 求点P的坐标;(3)、如图2,将△ACB绕点B顺时针方向旋转60°,得到△BGH,使点A与点H重合,点C与点G重合,将△BGH沿直线BC平移,记平移中的△BGH为△B′G′H′,在平移过程中,设直线B′H′与x轴交于点M,是否存在这样的点M,使得△B′MG′为等腰三角形?若存在,求出此时点M的坐标;若不存在,说明理由.