山东省济南市槐荫区2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-07-07 类型:期末考试
一、单选题
-
1. 下列各数中是无理数的是( )A、3.14 B、0 C、 D、2. 在平面直角坐标系中,点M(2,3)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 直角三角形的两直角边长分别为5和12,则斜边长为( )A、13 B、14 C、 D、14. 如果a>b,那么下列结论一定正确的是( )A、a+3<b+3 B、a-3<b-3 C、3a>3b D、-3a>-3b5. 下列各式是最简二次根式的是( )A、 B、 C、 D、6. 一组数据分别为:12,13,14,15,15.则这组数据的众数,中位数分别为( )A、12,14 B、14,15 C、15,14 D、15,127. 如图, 中, , 是 边上的中线,若 ,则 等于( )
 A、 B、 C、 D、8. 将点P(-5,4)向右平移4个单位,得到点P的对应点P′的坐标是( )A、(-5,8) B、(-1,4) C、(-9,4) D、(-5,0)9. 如图,一次函数y=2x+8的图象经过点A(-2,4),则不等式2x+8>4的解集是( )
A、 B、 C、 D、8. 将点P(-5,4)向右平移4个单位,得到点P的对应点P′的坐标是( )A、(-5,8) B、(-1,4) C、(-9,4) D、(-5,0)9. 如图,一次函数y=2x+8的图象经过点A(-2,4),则不等式2x+8>4的解集是( ) A、x<-2 B、x>-2 C、x<0 D、x>010. 如图,在中, , , , 则的长是( )
A、x<-2 B、x>-2 C、x<0 D、x>010. 如图,在中, , , , 则的长是( ) A、8 B、1 C、2 D、411. 若 , 则一次函数的图象大致是( )A、
A、8 B、1 C、2 D、411. 若 , 则一次函数的图象大致是( )A、 B、
B、 C、
C、 D、
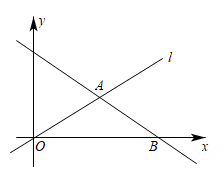
D、 12. 一次函数的图象与x轴、y轴分别交于点A、B,O为坐标原点,则在△OAB内部(包括边界),纵坐标、横坐标都是整数的点共有( )A、90个 B、92个 C、104个 D、106个
12. 一次函数的图象与x轴、y轴分别交于点A、B,O为坐标原点,则在△OAB内部(包括边界),纵坐标、横坐标都是整数的点共有( )A、90个 B、92个 C、104个 D、106个二、填空题
-
13. 25的算术平方根是 .14. 一次函数y=x+2的图象不经过第象限.15. 某中学为了选拔一名运动员参加市运会 米短比赛,有甲、乙两名运动员备选,他们最近测试的 次百米跑平均时间都是 秒,他们的方差分别是 (秒 ) (秒 ),如果要选择一名成绩优秀且稳定的人去参赛,应派去.16. 点 关于 轴对称的点的坐标为.17. 如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E,若BC=7,DE=3,则BD的长为 .
 18. 如图,把一副七巧板按如图进行1~7编号,1~7号分别对应着七巧板的七块,如果编号5对应的面积等于5cm2 , 则由这幅七巧板拼得的“房子”的面积等于cm2 .
18. 如图,把一副七巧板按如图进行1~7编号,1~7号分别对应着七巧板的七块,如果编号5对应的面积等于5cm2 , 则由这幅七巧板拼得的“房子”的面积等于cm2 .
三、解答题
-
19. 解方程组:20. 解不等式组:21. 如图,在Rt△ABC中,∠B=90°,AB=4,BC=3,阴影部分是一个长方形,AE=1,求阴影部分的面积.
 22. 如图所示,直线AB与x轴交于A,与y轴交于B.
22. 如图所示,直线AB与x轴交于A,与y轴交于B. (1)、请直接写出A,B两点的坐标:A , B;(2)、求直线AB的函数表达式;(3)、当x=5时,求y的值.23. 如图,OP是∠AOB的平分线,PC⊥OA,PD⊥OB,垂足分别为C,D.
(1)、请直接写出A,B两点的坐标:A , B;(2)、求直线AB的函数表达式;(3)、当x=5时,求y的值.23. 如图,OP是∠AOB的平分线,PC⊥OA,PD⊥OB,垂足分别为C,D. (1)、求证:OC=OD;(2)、求证:OP是CD的垂直平分线.24. 某校为了庆祝建国七十周年,决定举办一台文艺晚会,为了了解学生最喜爱的节目形式,随机抽取了部分学生进行调查,规定每人从“歌曲”,“舞蹈”,“小品”,“相声”和“其它”五个选项中选择一个,并将调查结果绘制成如下两幅不完整的统计图表,请根据图中信息,解答下列题:
(1)、求证:OC=OD;(2)、求证:OP是CD的垂直平分线.24. 某校为了庆祝建国七十周年,决定举办一台文艺晚会,为了了解学生最喜爱的节目形式,随机抽取了部分学生进行调查,规定每人从“歌曲”,“舞蹈”,“小品”,“相声”和“其它”五个选项中选择一个,并将调查结果绘制成如下两幅不完整的统计图表,请根据图中信息,解答下列题:最喜爱的节目
人数
歌曲
15
舞蹈
a
小品
12
相声
10
其它
b
 (1)、在此次调查中,该校一共调查了名学生;(2)、a=;b=;(3)、在扇形计图中,计算“歌曲”所在扇形的圆心角的度数;(4)、若该校共有1200名学生,请你估计最喜爱“相声”的学生的人数.25. 某社区拟建甲,乙两类摊位以激活“地摊经济”,1个甲类摊位和2个乙类摊位共占地面积14平方米,2个甲类摊位和3个乙类摊位共占地面积24平方米.(1)、求每个甲,乙类摊位占地面积各为多少平方米?(2)、该社区拟建甲,乙两类摊位共100个,且乙类摊位的数量不多于甲类摊位数量的3倍,求甲类摊位至少建多少个?
(1)、在此次调查中,该校一共调查了名学生;(2)、a=;b=;(3)、在扇形计图中,计算“歌曲”所在扇形的圆心角的度数;(4)、若该校共有1200名学生,请你估计最喜爱“相声”的学生的人数.25. 某社区拟建甲,乙两类摊位以激活“地摊经济”,1个甲类摊位和2个乙类摊位共占地面积14平方米,2个甲类摊位和3个乙类摊位共占地面积24平方米.(1)、求每个甲,乙类摊位占地面积各为多少平方米?(2)、该社区拟建甲,乙两类摊位共100个,且乙类摊位的数量不多于甲类摊位数量的3倍,求甲类摊位至少建多少个?