广东省中山市2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-07-07 类型：期末考试

进入出卷网下载

一、单选题

1. 某种芯片每个探针单元的面积为 $0.00000164 c m^{2}$ ，0.00000164用科学记数法可表示为（）

A、 $1.64 \times 10^{- 5}$ B、 $1.64 \times 10^{- 6}$ C、 $16.4 \times 10^{- 7}$ D、 $0.164 \times 10^{- 5}$

查看试题解析
2. 下面的图形是用数学家名字命名的，其中是轴对称图形的是（）

A、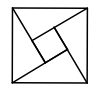赵爽弦图 B、费马螺线 C、科克曲线 D、斐波那契螺旋线

查看试题解析
3. 下列多项式中，能运用平方差公式分解因式的是（）

A、 $a^{2} + b^{2}$ B、 $2 a - 2 b$ C、 $- a^{2} + b^{2}$ D、 $- a^{2} - b^{2}$

查看试题解析
4. 计算： ${(- \frac{2}{3} x^{2} y)}^{3} =$ （）

A、 $- 2 x^{6} y^{3}$ B、 $\frac{8}{27} x^{6} y^{3}$ C、 $- \frac{8}{27} x^{5} y^{3}$ D、 $- \frac{8}{27} x^{6} y^{3}$

查看试题解析
5. 将分式 $\frac{x^{2}}{2 x + 2 y}$ 中的x，y同时扩大4倍，则分式的值（）

A、扩大4倍 B、扩大2倍 C、缩小到原来的一半 D、保持不变

查看试题解析
6. 已知 $x = 2$ 是分式方程 $\frac{k}{x} + \frac{x - 1}{x - 3} = 1$ 的解，那么k的值为（）

A、0 B、1 C、2 D、4

查看试题解析
7. 在 $△ A B C$ 中， $A B = A C$ ， $A D ⊥ B C$ 于点D，若 $A B = 8$ ， $C D = 5$ ，则 $△ A B C$ 的周长为（）

A、13 B、18 C、21 D、26

查看试题解析
8. 如图，点E在AC上，则 $∠ A + ∠ B + ∠ C + ∠ D + ∠ D E B$ 的度数是（）

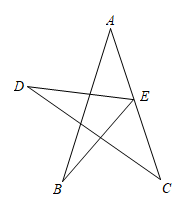A、90° B、180° C、270° D、360°

查看试题解析
9. 如图，两个正方形的边长分别为a、b，若 $a + b = 7$ ， $a b = 3$ ，则阴影部分的面积是（）

A、40 B、 $\frac{49}{2}$ C、20 D、23

查看试题解析
10. 如图，已知直角三角形ABC中，∠ACB=90°，∠CAB=60°，在直线BC或AC上取一点P，使得△ABP为等腰三角形，则符合条件的点有（）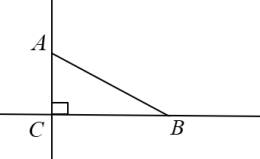

A、4个 B、5个 C、6个 D、7个

查看试题解析

二、填空题

11. 正五边形的外角和等于 ◦．

查看试题解析
12. 已知 $x^{2} - 2 x = - 1$ ，则代数式 $5 + x (x - 2)$ 的值为．

查看试题解析
13. 已知 $\frac{x - 3 y}{x} = 0$ ，则 $\frac{y}{x} =$ ．

查看试题解析
14. 如图， $∠ B = ∠ C$ ，译添加一个条件使得 $△ A B E ≌ △ A C D$ ．

查看试题解析
15. 分式方程： $\frac{x}{x - 1} + \frac{2}{1 - x} = 2$ 的解是．

查看试题解析
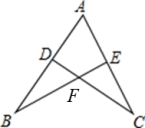16. 在 $△ A B C$ 中， $A B = A C$ ， AB的垂直平分线与AC所在直线相交所得的锐角为42°，则 $∠ B =$ ．

查看试题解析
17. 如图， $A B = A C = 5$ ， $∠ B A C = 110 °$ ， AD是∠BAC内的一条射线，且 $∠ B A D = 25 °$ ， P为AD上一动点，则 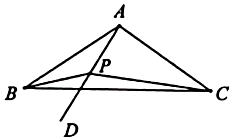$| P B - P C |$ 的最大值是．

查看试题解析

三、解答题

18. 计算： $(2 a - 3) (2 a + 3) - (5 a^{3} + a) \div a$ ．

查看试题解析
19. 已知 $\frac{m}{2} = \frac{n}{3}$ ，求 $(\frac{4 n^{2} - 4 m n}{m^{2}} + 1) \div \frac{2 n - m}{m}$ 的值．

查看试题解析
20. 如图，在平面直角坐标系中， $A (4 ， 1)$ ， $B (- 4 ， - 2)$ ， $C (1 ， - 3)$ ．
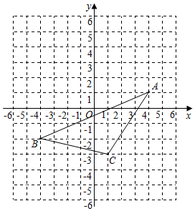
( 1 )作出 $△ A B C$ 关于x轴对称的图形 $△ A_{1} B_{1} C_{1}$ ，并写出点 $B_{1}$ 的坐标；
( 2 )在x轴上作出点P，使得 $P B + P C$ 最短，并写出点P的坐标．

查看试题解析
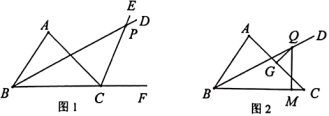
21. 在 $(x^{2} - 2 x + a) (3 x + b)$ 的运算结果中， $x^{2}$ 的系数为-4，x的系数为-7，求a，b的值并对式子 $4 a x^{2} + b^{2}$ 进行因式分解．

查看试题解析
22. 如图，AB，CD相交于点E且互相平分，F是BD延长线上一点，若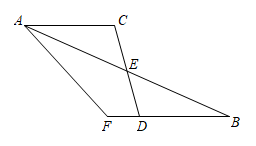 $∠ F A C = 2 ∠ B A C$ ，求证： $A C + D F = A F$ .

查看试题解析
23. 某商场计划在年前用30000元购进一批彩灯，由于货源紧张，厂商提价销售，实际的进货价格比原来提高了20%，结果比原计划少购进100盏彩灯．该商场实际购进彩灯的单价是多少元？

查看试题解析
24. 如图， $△ A B C$ 中， $A B = A C = B C = 20$ 厘米，如果点M从点C出发，点N从点B出发，沿着三角形三边以4厘米/秒的速度运动，当点N第一次到达C点时，M，N两点同时停止运动．运动时间为t（秒）．

(1)、当 $0 < t < 5$ 且 $△ B M N$ 为直角三角形时，求t的值；

(2)、当t为何值， $△ B M N$ 为等边三角形．

查看试题解析
25. 如图1，射线BD交△ABC的外角平分线CE于点P，已知∠A=78°，∠BPC=39°，BC=7，AB=4．

(1)、求证：BD平分∠ABC；

(2)、如图2，AC的垂直平分线交BD于点Q，交AC于点G，QM⊥BC于点M，求MC的长度．

查看试题解析