广东省肇庆市封开县2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-07-07 类型:期末考试
一、单选题
-
1. 手机已逐渐成为人们日常通讯的主要工具,其背后离不开通讯运营商的市场支持,下图展现的是我国四大通讯运营商的企业图标,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知三角形的两边长分别为2、10,则第三边长可能是( )A、6 B、8 C、10 D、123. 在 中, ,则 等于( )A、 B、 C、 D、4. 下图中的全等三角形是( )
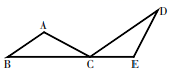
2. 已知三角形的两边长分别为2、10,则第三边长可能是( )A、6 B、8 C、10 D、123. 在 中, ,则 等于( )A、 B、 C、 D、4. 下图中的全等三角形是( )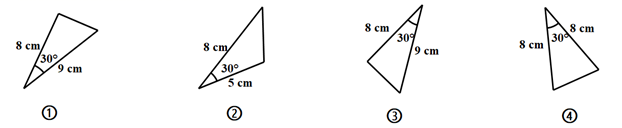 A、①和② B、②和③ C、②和④ D、①和③5. 下列运算正确的是( )A、 B、 C、 D、6. 如图,ABC中,AD平分∠BAC,AB=4,AC=2,若ACD的面积等于3,则ABD的面积为( )
A、①和② B、②和③ C、②和④ D、①和③5. 下列运算正确的是( )A、 B、 C、 D、6. 如图,ABC中,AD平分∠BAC,AB=4,AC=2,若ACD的面积等于3,则ABD的面积为( )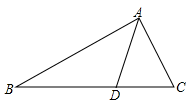 A、 B、4 C、6 D、127. 要使分式有意义,则x应满足的条件是( )A、 B、 C、 D、8. 关于x的二次三项式x2+ax+36能直接用完全平方公式分解因式,则a的值是( )A、﹣6 B、±6 C、12 D、±129. 若关于x 的方程 有增根,则m 的值是( )A、3 B、2 C、1 D、任意值10. 如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连结BF,CE.下列说法:①△ABD和△ACD面积相等;②∠BAD=∠CAD;③△BDF≌△CDE;④BF∥CE;⑤CE=AE.其中正确的有( )
A、 B、4 C、6 D、127. 要使分式有意义,则x应满足的条件是( )A、 B、 C、 D、8. 关于x的二次三项式x2+ax+36能直接用完全平方公式分解因式,则a的值是( )A、﹣6 B、±6 C、12 D、±129. 若关于x 的方程 有增根,则m 的值是( )A、3 B、2 C、1 D、任意值10. 如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连结BF,CE.下列说法:①△ABD和△ACD面积相等;②∠BAD=∠CAD;③△BDF≌△CDE;④BF∥CE;⑤CE=AE.其中正确的有( )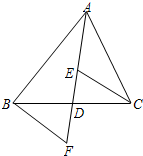 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 因式分解: .12. 已知一个多边形的内角和是1080°,这个多边形外角和是13. 如图:在中, , 以顶点C为圆心,适当长为半径画弧,分别交、于点E、F,再分别以点E、F为圆心,大于的长为半径画弧,两弧交于点P,作射线交于点D,若 , , 则的面积为.
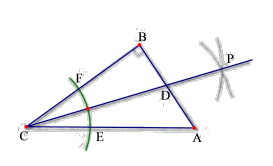 14. , , 则 .15. 如图,在ABC中,AC⊥BC,∠B=30°,CD⊥AB,垂足为D,若AD=1,则AB的长为 .
14. , , 则 .15. 如图,在ABC中,AC⊥BC,∠B=30°,CD⊥AB,垂足为D,若AD=1,则AB的长为 .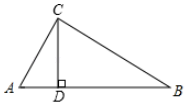 16. 如图,在△ACD中, , AC=6,AD=8, , E是CD上一点,BE交AD于点F,若EF=BF,则图中阴影部分的面积为 .
16. 如图,在△ACD中, , AC=6,AD=8, , E是CD上一点,BE交AD于点F,若EF=BF,则图中阴影部分的面积为 .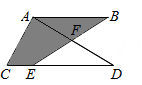 17. 已知: , 则代数式 .
17. 已知: , 则代数式 .三、解答题
-
18. 计算: .19. 解方程:20. 已知:如图,C为线段BE上一点,AB∥DC,AB=EC,BC=CD.求证:∠ACD=∠E.
 21. 先化简,再求值: , 其中 .22. 如图,已知ABC,以A为圆心,AC为半径画弧与BC相交于另一点E.
21. 先化简,再求值: , 其中 .22. 如图,已知ABC,以A为圆心,AC为半径画弧与BC相交于另一点E.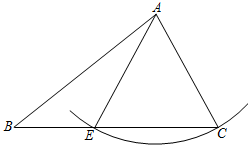 (1)、用尺规作图的方法,作出ABC的高AD(垂足为D).(2)、求证:ED=CD.23. 某单位计划在室内安装空气净化装置,需购进A,B两种设备.已知每台B种设备比每台A种设备价格多0.6万元,花5万元购买A种设备和花11万元购买B种设备的数量相同.(1)、求A,B两种设备每台各多少万元.(2)、根据单位实际情况,需购进A,B两种设备共18台,总费用不高于14万元.求A种设备至少要购买多少台?24. 如图,点C为线段AB上一点,以线段AC为腰作等腰直角△ACD,∠ACD=90°,点E为CD延长线上一点,且CE=CB,连接AE,BD,点F为AE延长线上一点,连接BF,FD.
(1)、用尺规作图的方法,作出ABC的高AD(垂足为D).(2)、求证:ED=CD.23. 某单位计划在室内安装空气净化装置,需购进A,B两种设备.已知每台B种设备比每台A种设备价格多0.6万元,花5万元购买A种设备和花11万元购买B种设备的数量相同.(1)、求A,B两种设备每台各多少万元.(2)、根据单位实际情况,需购进A,B两种设备共18台,总费用不高于14万元.求A种设备至少要购买多少台?24. 如图,点C为线段AB上一点,以线段AC为腰作等腰直角△ACD,∠ACD=90°,点E为CD延长线上一点,且CE=CB,连接AE,BD,点F为AE延长线上一点,连接BF,FD.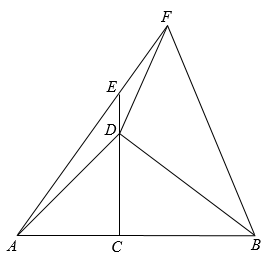 (1)、①求证:△ACE≌△DCB;
(1)、①求证:△ACE≌△DCB;②试判断BD与AF的位置关系,并证明;
(2)、若BD平分∠ABF,当CD=3DE,S△ADE , 求线段BF的长.25. 在平面直角坐标系中,点 , , 在y轴负半轴上取点E,使 , 作 , 直线交的延长线于点D.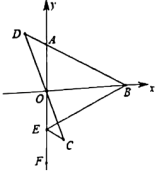 (1)、根据题意,可求得;(2)、求证:;(3)、动点P从E出发沿路线运动速度为每秒1单位,到B点处停止运动;动点Q从B出发沿运动速度为每秒3个单位,到E点处停止运动.二者同时开始运动,都要到达相应的终点才能停止.在某时刻,作于点M,于点N.问两动点运动多长时间与全等?
(1)、根据题意,可求得;(2)、求证:;(3)、动点P从E出发沿路线运动速度为每秒1单位,到B点处停止运动;动点Q从B出发沿运动速度为每秒3个单位,到E点处停止运动.二者同时开始运动,都要到达相应的终点才能停止.在某时刻,作于点M,于点N.问两动点运动多长时间与全等?