广东省深圳市南山区2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-07-07 类型：期末考试

进入出卷网下载

一、单选题

1. 下列线段能组成直角三角形的一组是（）

A、1，2，2 B、3，4，5 C、 $\sqrt{3}$ ，2， $\sqrt{5}$ D、5，6，7

查看试题解析
2. 在如图所示的直角坐标系中，M，N的坐标分别为（）

A、M（2，-1），N（2，1） B、M（-1，2），N（2，1） C、M（-1，2），N（1，2） D、M（2，-1），N（1，2）

查看试题解析
3. 在一次投篮训练中，甲、乙、丙、丁四人各进行10次投篮，每人投篮成绩的平均数都是8，方差分别为S_甲²＝0.24，S_乙²＝0.42，S_丙²＝0.56，S_丁²＝0.75，成绩最稳定的是（）

A、甲． B、乙 C、丙 D、丁

查看试题解析
4. 若a＜ $\sqrt{7}$ ＜b ，且a与b为连续整数，则a与b的值分别为（　　）

A、1；2 B、2；3 C、3；4 D、4；5

查看试题解析
5. 将一副三角板（ $∠ A ＝ 30 ° ， ∠ E ＝ 45 °$ ）按如图所示方式摆放，使得 $B A / / E F$ ，则 $∠ A O F$ 等于（）

A、 $75 °$ B、 $90 °$ C、 $105 °$ D、 $115 °$

查看试题解析
6. 下列计算结果，正确的是（）

A、 $\sqrt{{(－ 3)}^{2}}$ ＝－3 B、 $\sqrt{2}$ ＋ $\sqrt{5}$ ＝ $\sqrt{7}$ C、 $2 \sqrt{3}$ － $\sqrt{3}$ ＝1 D、 ${(\sqrt{5})}^{2}$ ＝5

查看试题解析
7. 一次函数 $y = k x + b$ 的图象如图所示，则下列结论正确的是（）

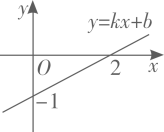A、 $k < 0$ B、 $b = - 1$ C、 $y$ 随 $x$ 的增大而减小 D、当 $x > 2$ 时， $k x + b < 0$

查看试题解析
8. 下列命题错误的个数有（　　）
①实数与数轴上的点一一对应；②无限小数就是无理数；③三角形的一个外角大于任何一个和它不相邻的内角；④两条直线被第三条直线所截，同旁内角互补．

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 勾股定理是几何中的一个重要定理，在我国算书《网醉算经》中就有“若勾三，股四，则弦五”的记载．如图1，是由边长相等的小正方形和直角三角形构成的，可以用其面积关系验证勾股定理．图2是由图1放入矩形内得到的，∠BAC=90°，AB=3，BC=5，点D，E，F，G，H，I都在矩形KLMJ的边上，则矩形KLMJ的面积为（）

A、121 B、110 C、100 D、90

查看试题解析
10. A，B两地相距640km，甲、乙两辆汽车从A地出发到B地，均匀速行驶，甲出发1小时后，乙出发沿同一路线行驶，设甲、乙两车相距s（km），甲行驶的时间为t（h），s与t的关系如图所示，下列说法：
①甲车行驶的速度是60km/h，乙车行驶的速度是80km/h；②乙出发4h后追上甲；③甲比乙晚到 $\frac{5}{3}$ h；④甲车行驶8h或9 $\frac{1}{3}$ h，甲，乙两车相距80km；其中正确的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 若二次根式 $\sqrt{x - 5}$ 有意义，则x的取值范围是.

查看试题解析
12. 将直线y＝3x向上平移3个单位，得到直线．

查看试题解析
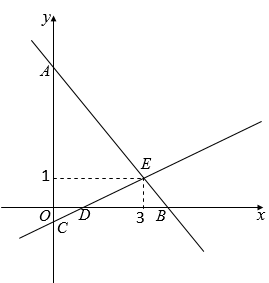13. 如图，直线 $A B ： y = k x + b$ 与直线 $C D ： y = m x + n$ 交于点E(3，1)，则关于x，y的二元一次方程组 ${\begin{array}{l} y = k x + b \\ y = m x + n \end{array}$ 的解为．

查看试题解析
14. 已知M（2n－m，5）和N（13，m）关于x轴对称，则（m＋n）²⁰²²的值为．

查看试题解析
15. 如图，在直角坐标系中，矩形ABCO的边OA在x轴上，边OC在y轴上，点B的坐标为（4，8），将矩形沿对角线AC翻折，B点落在D点的位置，且AD交y轴于点E，那么点D的坐标为．

查看试题解析

三、解答题

16. 计算及解方程组：

(1)、 $\sqrt{12}$ × $\sqrt{3}$ ；

(2)、 $\frac{\sqrt{20} ＋ \sqrt{5}}{\sqrt{5}}$ －2；

(3)、( $\sqrt{3}$ ＋ $\sqrt{2}$ )( $\sqrt{3}$ － $\sqrt{2}$ )＋ $\sqrt{8}$ － $\sqrt{\frac{1}{2}}$ ；

(4)、 ${\begin{array}{l} m － \frac{n}{2} ＝ 2 \\ 2 m ＋ 3 n ＝ 12 \end{array}$ ．

查看试题解析
17. 深圳市近期正在创建第六届全国文明城市，学校倡议学生利用双休日参加义工活动，为了解同学们的活动情况学校随机调查了部分同学的活动时间，并用得到的数据绘制了不完整的统计图，根据图中信息回答下列问题：

(1)、将条形统计图补充完整；

(2)、扇形图中“1.5小时”部分圆心角是多少度，活动时间的平均数是多少个小时，众数是多少小时，中位数是多少个小时；

(3)、若该学校共有900人参与义工活动，请你估计工作时长一小时以上（不包括一小时）的学生人数．

查看试题解析
18. 在我国古代数学著作《九章算术》中记载了一个有趣的问题，这个问题的意思是：有一个水池，水面是一个边长为10尺的正方形，在水池正中央有一根新生的芦苇，它高出水面1尺，如图所示，如果把这根芦苇垂直拉向岸边，它的顶端恰好到达岸边的水面．那么水深多少？芦苇长为多少？

查看试题解析
19. 为了响应市委和市政府“绿色环保，节能减排”的号召，幸福商场用3300元购进甲、乙两种节能灯共计100只，很快售完.这两种节能灯的进价、售价如表所示：

进价（元/只）
售价（元/只）
甲种节能灯
30
40
乙种节能灯
35
50

(1)、求幸福商场甲、乙两种节能灯各购进了多少只?

(2)、全部售完100只节能灯后，商场共计获利多少元?

查看试题解析
20. 在如图的直角坐标系中，每个小方格都是边长为1个单位的正方形，△ABC的三个顶点都在格点上（每个小方格的顶点叫格点），点A的坐标为（-2，3）．

( 1 )请画出△ABC关于x轴对称的 $△ A^{'} B^{'} C^{'}$ （不写画法，其中 $A ′ ， B ′ ， C ′$ 分别是A，B，C的对应点）；

( 2 )直接写出 $A ′ ， B ′ ， C ′$ 三点的坐标： $A ′$ （）， $B ′$ （）， $C^{'}$ （）；

( 3 )在y轴上求作一点P，使PA＋PB的值最小．（简要写出作图步骤）

查看试题解析
21. 【问题背景】∠MON＝90°，点A、B分别在OM、ON上运动（不与点O重合）．

(1)、【问题思考】如图①，AE、BE分别是∠BAO和∠ABO的平分线，随着点A、点B的运动，∠AEB＝．

(2)、如图②，若BC是∠ABN的平分线，BC的反向延长线与∠OAB的平分线交于点D．
①若∠BAO＝70°，则∠D＝°．

②随着点A、B的运动，∠D的大小会变吗？如果不会，求∠D的度数；如果会，请说明理由；

(3)、【问题拓展】在图②的基础上，如果∠MON＝a，其余条件不变，随着点A、B的运动（如图③），∠D＝.（用含a的代数式表示）

查看试题解析
22. 如图，在平面直角坐标系中，直线AB：y＝kx＋1（k≠0）交y轴于点A，交x轴于点B（3，0），点P是直线AB上方第一象限内的动点．

(1)、求直线AB的表达式和点A的坐标；

(2)、点P是直线x＝2上一动点，当△ABP的面积与△ABO的面积相等时，求点P的坐标；

(3)、当△ABP为等腰直角三角形时，请直接写出点P的坐标．

查看试题解析

	进价（元/只）	售价（元/只）
甲种节能灯	30	40
乙种节能灯	35	50