广东省深圳市龙华区2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-07-07 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各数中，是无理数的是（　　）

A、﹣2 B、 $\sqrt{3}$ C、 $\frac{7}{3}$ D、3.14

查看试题解析
2. 家长会前，四个孩子分别向家长描述自己在班里的座位，家长能准确找到自己孩子座位的是（　　）

A、小明说他坐在第1排 B、小白说他坐在第3列 C、小清说她坐在第2排第5列 D、小楚说他的座位靠窗

查看试题解析
3. 下列各组数据中，不能作为直角三角形边长的是（）

A、3，5，7 B、6，8，10 C、5，12，13 D、1，2， $\sqrt{3}$

查看试题解析
4. 如图1， $\sqrt{15}$ 在数轴对应的点可能是（　　）

A、点A B、点B C、点C D、点D

查看试题解析
5. 某运动品牌旗舰店统计了某款运动服11月份的销售情况，绘制成了如图所示的统计图，经过分析，该店店长决定12月份采购该款式更多的蓝色型号运动服，这一决定主要依据销售数据中的（　　）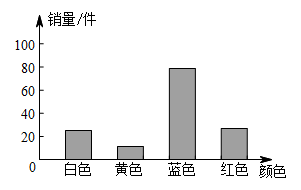

A、众数 B、方差 C、中位数 D、平均数

查看试题解析
6. 如图，直线l₁：y＝x+2与直线l₂：y＝kx+b相交于点P（m，4），则方程组 ${\begin{array}{l} y = x + 2 \\ y = k x + b \end{array}$ 的解是（　　）

A、 ${\begin{array}{l} x = 2 \\ y = 0 \end{array}$ B、 ${\begin{array}{l} x = 0 \\ y = 4 \end{array}$ C、 ${\begin{array}{l} x = 4 \\ y = 2 \end{array}$ D、 ${\begin{array}{l} x = 2 \\ y = 4 \end{array}$

查看试题解析
7. 下列说法错误的是（　　）

A、16的算术平方根是4 B、三角形的一个外角等于任意两个内角之和 C、一次函数y＝﹣2x+3的图象不经过第三象限 D、在平面直角坐标系中，若一个点的坐标为（3，0），则这个点在x轴上

查看试题解析
8. 《孙子算经》中有一道题，原文是：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何？”意思是：用一根绳子去量一根长木，绳子还剩余4.5尺；将绳子对折再量长木，长木还剩余1尺，问长木多少尺？如果设长木长x尺，绳长y尺，则可以列方程组（）

A、 ${\begin{array}{l} y - x = 4.5 \\ \frac{1}{2} y - x = 1 \end{array}$ B、 ${\begin{array}{l} x - y = 4.5 \\ \frac{1}{2} y - x = 1 \end{array}$ C、 ${\begin{array}{l} x - y = 4.5 \\ x - \frac{1}{2} y = 1 \end{array}$ D、 ${\begin{array}{l} y - x = 4.5 \\ x - \frac{1}{2} y = 1 \end{array}$

查看试题解析
9. 如图①是某公共汽车线路收支差额y（票价总收入减去运营成本）与乘客量x的函数图象，目前这条线路亏损，为了扭亏，有关部门举行提高票价的听证会，乘客代表认为：公交公司应降低运营成本，实现扭亏；公交公司认为：运营成本难以下降，提高票价才能扭亏；根据这两种意见，把图①分别改画成图②和图③，则下列判断不合理的是（　　）

A、图①中点A的实际意义是公交公司运营前期投入成本为1万元 B、图②能反映公交公司意见 C、图③能反映乘客意见 D、图②中当乘客量为1.5万时公交公司收支平衡

查看试题解析
10. 如图，Rt△ABC中，∠C＝90°，AC＝BC，点D、E分别是边AB、AC上的点，把△ADE沿DE折叠，点A恰好落在BC上的点F处，若点F为BC的中点，则 $\frac{C E}{A C}$ 的值是（　　）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{2}{5}$ D、 $\frac{3}{8}$

查看试题解析

二、填空题

11. 在平面直角坐标系中，点P（2，﹣5）到y轴的距离是．

查看试题解析
12. 甲、乙、丙三位同学参加演讲比赛，经过三轮比赛后，三人的成绩平均分相同，方差分别是S甲²＝1.2，S乙²＝3.3，S丙²＝1.5．你认为成绩比较稳定的是（填“甲”或“乙”或“丙”）．

查看试题解析
13. 将一把直尺与含30°的直角三角板如图摆放，使三角板的一个锐角顶点落在直尺的一边上，若∠1＝40°，则∠2＝°．

查看试题解析
14. 如图，BD和CD是△ABC的角平分线，∠BDC＝118°，则∠BAC＝°．

查看试题解析
15. 如图1，动点P从长方形ABCD的顶点A出发，沿A→C→D以1cm/s的速度运动到点D停止．设点P的运动时间为x（s），△PAB的面积为y（cm²）．表示y与x的函数关系的图象如图2所示，则长方形ABCD的面积为 cm² ．

查看试题解析

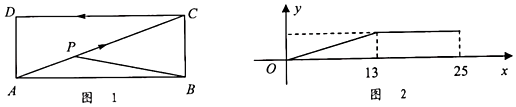
三、解答题

16. 计算题

(1)、 $\frac{\sqrt{3} \times \sqrt{6}}{\sqrt{2}} + \sqrt[3]{- 8}$ ；

(2)、 $(3 + \sqrt{2}) (3 - \sqrt{2}) - \frac{\sqrt{12} + \sqrt{27}}{\sqrt{3}}$ ．

查看试题解析
17. 解方程组

(1)、 ${\begin{array}{l} x = 2 y \\ x - y = 6 \end{array}$ ；

(2)、 ${\begin{array}{l} \frac{1}{3} x + 1 = 2 y \\ 2 x - 3 y = 3 \end{array}$ ．

查看试题解析
18. 为迎接中国共产党建党100周年，某校组织七、八年级学生开展了党史知识竞赛．现从两个年级各随机抽取15名学生的竞赛成绩（百分制）进行分析，过程如下：
【收集数据】
七年级：89，74，85，80，81，92，58，99，80，82，90，76，80，85，64．
八年级：91，72，92，80，83，92，88，82，85，83，76，83，82，80，46．
【整理数据】

40≤x＜50
50≤x＜60
60≤x＜70
70≤x＜80
80≤x＜90
90≤x＜100
七年级
0
1
1
2
8
3
八年级
1
0
0
a
b
3
【分析数据】

平均数
众数
中位数
七年级
81
c
81
八年级
81
83
d
【应用数据】

(1)、由如表填空：a＝， b＝， c＝， d＝．

(2)、若八年级有500名学生，请你估计该校八年级学生在本次竞赛中成绩在90分以上（含90分）的有人．

(3)、你认为哪个年级的学生对党史知识掌握的总体水平较好，并说明理由．

查看试题解析

四、八年级的平均成绩相等，而八年级的中位数为83，七年级的中位数为81，83>81 八年级的学生对党史知识掌握的总体水平较好（答案不唯一，合理即可）

19. 如图，在△ABC中，∠ACB的平分线CD交AB于点D，E为AC边上一点，且满足∠AED＝2∠DCB．

(1)、求证：DE∥BC；

(2)、若∠B＝90°，AD＝6，AE＝9，求CE的长．

查看试题解析
20. 天虹商场购进A、B两种运动服进行销售，若购进A运动服3件，B运动服2件，共花费340元；若购进A运动服2件，B运动服3件，共花费360元．销售时，两种运动服都是在进价基础上提高40元/件进行标价，再打八折销售．

(1)、求A、B两种运动服每件的进价分别是多少元？

(2)、若实际购进两种运动服共100件，其中A运动服a件，全部售完后获利w元，请求出w与a之间的函数关系式．

查看试题解析
21. 小明在学习一次函数后，对形如y＝k（x﹣m）+n（其中k，m，n为常数，且k*≠0）的一次函数图象和性质进行了探究，过程如下：

(1)、【特例探究】如图所示，小明分别画出了函数y＝（x﹣1）+2，y＝﹣（x﹣1）+2，y＝2（x﹣1）+2的图象．
请你根据列表、描点、连线的步骤在图中画出函数y＝﹣2（x﹣1）+2的图象．

(2)、【深入探究】通过对上述几个函数图象的观察、思考，你发现y＝k（x﹣1）+2（k为常数，且k≠0）的图象一定会经过的点的坐标是．

(3)、【得到性质】函数y＝k（x﹣m）+n（其中k、m、n为常数，且k≠0）的图象一定会经过的点的坐标是．

(4)、【实践运用】已知一次函数y＝k（x+2）+3（k为常数，且k≠0）的图象一定过点N，且与y轴相交于点A，若△OAN的面积为2，则k的值为．

查看试题解析
22. 阅读材料：如图1，已知Rt△ABC中，∠C＝90°，请用尺规作图在AB边上求作点P，使得∠BPC+∠ACP＝90°．
小明提出想法：如图2，假设点P为所求作的点，连接CP，此时有∠BPC+∠ACP＝90°，因为∠BCP+∠ACP＝90°，所以∠BPC＝∠BCP，从而得到：BP＝BC．
由此想法得到如下作图方法：如图2，以点B为圆心，BC为半径画弧，该弧与AB相交于点P，则点P即为所作的点．
根据以上材料，完成下面两个问题：

(1)、请你类比上述作图方法，在图2中，用尺规作图在AB边上求作点Q，使得∠CQB+∠A＝180°．

(2)、在（1）的条件下，
①若AC＝6，AB＝10，求PQ的长．
②请直接写出∠PCQ与∠B之间的数量关系是　．

查看试题解析

	40≤x＜50	50≤x＜60	60≤x＜70	70≤x＜80	80≤x＜90	90≤x＜100
七年级	0	1	1	2	8	3
八年级	1	0	0	a	b	3

	平均数	众数	中位数
七年级	81	c	81
八年级	81	83	d