广东省深圳市宝安区2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-07-07 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各数中，是无理数的是（）

A、 $3 . \overset{\cdot}{1} \overset{\cdot}{4}$ B、 $π$ C、 $\frac{3}{8}$ D、 $\sqrt{9}$

查看试题解析
2. 若点 $P (m ， - 2)$ 在第三象限内，则m的值可以是（）

A、2 B、0 C、 $- 2$ D、 $\pm 2$

查看试题解析
3. 下列计算中，正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $3 + 2 \sqrt{3} = 5 \sqrt{3}$ C、 $\sqrt{3} \times \sqrt{6} = 3 \sqrt{2}$ D、 $2 \sqrt{3} - 2 = \sqrt{3}$

查看试题解析
4. 下列各组数中，不能作为直角三角形的三边的是（　　）

A、3，4，5 B、2，3， $\sqrt{5}$ C、8，15，17 D、3² ， 4² ， 5²

查看试题解析
5. 如图，将一副三角板平放在一平面上（点D在 $B C$ 上），则 $∠ 1$ 的度数为（）

A、 $60 °$ B、 $75 °$ C、 $90 °$ D、 $105 °$

查看试题解析
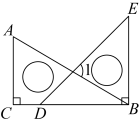6. 生活中常见的探照灯、汽车大灯等灯具都与抛物线有关．如图，从光源P点照射到抛物线上的光线 $P A ， P B$ 等反射以后沿着与直线 $P F$ 平行的方向射出，若 $∠ C A P = α °$ ， $∠ D B P = β °$ ，则 $∠ A P B$ 的度数为（）°

A、 $2 α$ B、 $2 β$ C、 $α + β$ D、 $\frac{5}{4} (α + β)$

查看试题解析
7. 下列命题正确的是（　　）

A、数轴上的每一个点都表示一个有理数 B、甲、乙两人五次考试平均成绩相同，且S_甲²＝0.9，S_乙²＝1.2，则乙的成绩更稳定 C、三角形的一个外角大于任意一个内角 D、在平面直角坐标系中，点（4，﹣2）与点（4，2）关于x轴对称

查看试题解析
8. 如图，已知点 $B (1 ， 2)$ 是一次函数 $y = k x + b (k \neq 0)$ 上的一个点，则下列判断正确的是（）

A、 $k > 0 ， b > 0$ B、y随x的增大而增大 C、当 $x > 0$ 时， $y < 0$ D、关于x的方程 $k x + b = 2$ 的解是 $x = 1$

查看试题解析
9. 某学校体育场的环形跑道长250m，甲、乙分别以一定的速度练习长跑和骑自行车，同时同地出发，如果反向而行，那么他们每隔20s相遇一次．如果同向而行，那么每隔50s乙就追上甲一次，设甲的速度为xm/s，乙的速度为ym/s，则可列方程组为（　　）

A、 ${\begin{array}{l} 20 (x + y) = 250 \\ 50 (y - x) = 250 \end{array}$ B、 ${\begin{array}{l} 20 (y - x) = 250 \\ 50 (x + y) = 250 \end{array}$ C、 ${\begin{array}{l} 20 (x - y) = 500 \\ 50 (x + y) = 250 \end{array}$ D、 ${\begin{array}{l} 20 (x + y) = 250 \\ 50 (y - x) = 500 \end{array}$

查看试题解析
10. 如图，直线 $y = - \frac{4}{3} x + 4$ 与x轴交于点B，与y轴交于点C，点 $E (1 ， 0)$ ， D为线段 $B C$ 的中点，P为y轴上的一个动点，连接 $P D$ 、 $P E$ ，当 $△ P E D$ 的周长最小时，点P的坐标为（）

A、 $(0 ， \frac{4}{5})$ B、 $(0 ， 1)$ C、 $(1 ， 0)$ D、 $(0 ， \frac{3}{2})$

查看试题解析

二、填空题

11. 9的算术平方根是．

查看试题解析
12. 为了庆祝中国共产党成立100周年，某校举行“歌唱祖国”班级合唱比赛，评委将从“舞台造型、合唱音准和进退场秩序”这三项进行打分，各项成绩均按百分制计算，然后再按舞台造型占40%，合唱音准占40%，进退场秩序占20%计算班级的综合成锁．七（1）班三项成绩依次是95分、90分、95分，则七（1）班的综合成绩为．

查看试题解析
13. 如图，长方形 $A B C D$ 的边 $A B$ 落在数轴上，A、B两点在数轴上对应的数分别为 $- 1$ 和1， $B C = 1$ ，连接 $B D$ ，以B为圆心， $B D$ 为半径画弧交数轴于点E，则点E在数轴上所表示的数为．

查看试题解析
14. 如图，若一次函数 $y = k x + 3$ 与正比例函数 $y = 2 x$ 的图象交于点 $(1 ， m)$ ，则方程组 ${\begin{array}{l} k x - y = - 3 \\ 2 x - y = 0 \end{array}$ 的解为．

查看试题解析
15. 如图，将长方形纸片ABCD沿MN折叠，使点A落在BC边上点A^'处，点D的对应点为D^' ，连接A'D^'交边CD于点E，连接CD^' ，若AB＝9，AD＝6，A'点为BC的中点，则线段ED'的长为．

查看试题解析

三、解答题

16. 计算： $(\sqrt{6} + \sqrt{12}) \times \sqrt{3} + \sqrt[3]{- 27}$

查看试题解析
17. 解方程组： ${\begin{array}{l} 2 x - y = 2 \\ 2 x - 6 y = 3 \end{array}$

查看试题解析
18. 深圳市教育局印发的《深圳市义务教育阶段学校课后服务实施意见》明确中小学课后延时服务从2021年3月5日开始实施某校积极开展课后延时服务活动，提供了“有趣的生物实验、经典影视欣赏、虚拟机器人竞赛、趣味篮球训练、国际象棋大赛……”等课程供学生自由选择．一个学期后，该校现为了解学生对课后延时服务的满意情况，随机对部分学生进行问卷调查，并将调查结果按照“A．非常满意；B．比较满意；C．基本满意；D．不满意”四个等级绘制成了如图所示的两幅不完整的统计图：
请你根据图中信息，解答下列问题：

(1)、该校抽样调查的学生人数为人，请补全条形统计图；

(2)、样本中，学生对课后延时服务满意情况的“中位数”所在等级为， “众数”所在等级为；（填“A、B、C或D”）

(3)、若该校共有学生2100人，据此调查估计全校学生对延时服务满意（包含A、B、C三个等级）的学生有人．

查看试题解析
19. 列方程组解应用题：全自动红外体温检测仪是一种非接触式人体测温系统，通过人体温度补偿、温度自动校正等技术实现准确、快速的测温工作，具备人体非接触测温、高温报警等功能．为了提高体温检测效率，某医院引进了一批全自动红外体温检测仪．通过一段时间使用发现，全自动红外体温检测仪的平均测温用时比人工测温快2秒，全自动红外体温检测仪检测60个人的体温的时间比人工检测40个人的体温的时间还少50秒，请计算全自动红外体温检测仪和人工测量测温的平均时间分别是多少秒？

查看试题解析
20. 如图， $l_{1}$ 表示星月公司某种电子产品的销售收入与销售量之间的关系， $l_{2}$ 表示该电子产品的生产成本与销售量之间的关系．

(1)、当销售量为件时，销售收入等于生产成本．

(2)、当 $x = 6$ 时，生产成本=万元．

(3)、若星月公司要想获得不低于22万元的利润，那么销售量至少为多少件？

查看试题解析
21. 定义：我们把一次函数 $y = k x + b (k \neq 0)$ 与正比例函数 $y = x$ 的交点称为一次函数 $y = k x + b (k \neq 0)$ 的“不动点”．例如求 $y = 2 x - 1$ 的“不动点”；联立方程 ${\begin{array}{l} y = 2 x - 1 \\ y = x \end{array}$ ，解得 ${\begin{array}{l} x = 1 \\ y = 1 \end{array}$ ，则 $y = 2 x - 1$ 的“不动点”为 $(1 ， 1)$ ．

(1)、由定义可知，一次函数 $y = 3 x + 2$ 的“不动点”为．

(2)、若一次函数 $y = m x + n$ 的“不动点”为 $(2 ， n - 1)$ ，求m、n的值．

(3)、若直线 $y = k x - 3 (k \neq 0)$ 与x轴交于点A，与y轴交于点B，且直线 $y = k x - 3$ 上没有“不动点”，若P点为x轴上一个动点，使得 $S_{△ A B P} = 3 S_{△ A B O}$ ，求满足条件的P点坐标．

查看试题解析
22.

(1)、【问题背景】学校数学兴趣小组在专题学习中遇到一个几何问题：如图1，已知等边△ABC，D是△ABC外一点，连接AD、CD、BD，若∠ADC＝30°，AD＝3，BD＝5，求CD的长．该小组在研究如图2中△OMN≌△OPQ中得到启示，于是作出图3，从而获得了以下的解题思路，请你帮忙完善解题过程．
解：如图3所示，以DC为边作等边△CDE，连接AE．
∵△ABC、△DCE是等边三角形，
∴BC＝AC，DC＝EC，∠BCA＝∠DCE＝60°．
∴∠BCA+∠ACD＝                  ▲                   +∠ACD，
∴∠BCD＝∠ACE，
∴                  ▲                   ，
∴AE＝BD＝5．
∵∠ADC＝30°，∠CDE＝60°，
∴∠ADE＝∠ADC+∠CDE＝90°．
∵AD＝3，
∴CD＝DE＝                  ▲                   ．

(2)、【尝试应用】如图4，在△ABC中，∠ABC＝45°，AB＝ $\sqrt{2}$ ， BC＝4，以AC为直角边，A为直角顶点作等腰直角△ACD，求BD的长．

(3)、【拓展创新】如图5，在△ABC中，AB＝4，AC＝8，以BC为边向外作等腰△BCD，BD＝CD，∠BDC＝120°，连接AD，求AD的最大值．

查看试题解析