广东省揭阳市普宁市2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-07-07 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各数中，不是无理数的是（　　）

A、3.1415926 B、0.020020002…（后面每两个2之间比前面多1个0） C、 $\sqrt{2}$ D、π

查看试题解析
2. 在平面直角坐标系中，已知点A（3，﹣2），则点A关于x轴对称的点A′坐标为（　　）

A、（﹣3，2） B、（3，2） C、（﹣3，﹣2） D、（3，﹣2）

查看试题解析
3. 北京今年6月某日部分区县的高气温如下表：
区县大兴通州平谷顺义怀柔门头沟延庆昌平密云房山
最高气温 32 32 30 32 30 32 29 32 30 32
则这10个区县该日最高气温的众数和中位数分别是（　　）

A、32，32 B、32，30 C、30，32 D、32，31

查看试题解析
4. 若代数式 $\sqrt{x - 2}$ 在实数范围内有意义，则x的取值范围是（　　）

A、x＜2 B、x＞2 C、x≥2 D、x≤2

查看试题解析
5. 如图，在△DEF中，点C在DF的延长线上，点B在EF上，且AB∥CD，∠EBA＝60°，则∠E+∠D的度数为（　　）

A、60° B、30° C、90° D、80°

查看试题解析
6. 满足下列条件的△ABC，不是直角三角形的是（）

A、b²﹣c²＝a² B、a：b：c＝3：4：5 C、∠C＝∠A﹣∠B D、∠A：∠B：∠C＝9：12：15

查看试题解析
7. 如图，圆柱的底面半径为 $\frac{6}{π}$ cm，AC是底面圆的直径，点P是BC上一点，且PC＝4cm，一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是（　　）

A、4 $\sqrt{5}$ cm B、2 $\sqrt{13}$ cm C、5 $\sqrt{6}$ cm D、10cm

查看试题解析
8. 对于一次函数y＝﹣2x+4，下列结论错误的是（　　）

A、函数的图象不经过第三象限 B、函数的图象与y轴的交点坐标是（0，4） C、函数的图象经过点（1，2） D、若两点A（1，y₁），B（3，y₂）在该函数图象上，则y₁＜y₂

查看试题解析
9. 我国古代《四元玉鉴》中记载“二果问价”问题，其内容如下：九百九十九文钱，甜果苦果买一千，甜果九个十一文，苦果七个四文钱，试问甜苦果几个，又问各该几个钱？若设买甜果x个，买苦果y个，则下列关于x、y的二元一次方程组中正确的是（　　）

A、 ${\begin{array}{l} x + y = 999 \\ \frac{11}{9} x + \frac{4}{7} y = 1000 \end{array}$ B、 ${\begin{array}{l} x + y = 1000 \\ \frac{11}{9} x + \frac{4}{7} y = 999 \end{array}$ C、 ${\begin{array}{l} x + y = 999 \\ \frac{9}{11} x + \frac{7}{4} y = 1000 \end{array}$ D、 ${\begin{array}{l} x + y = 1000 \\ \frac{9}{11} x + \frac{7}{4} y = 999 \end{array}$

查看试题解析
10. 如图，在△ABC中，∠ACB＞∠B，AD平分∠BAC，点E在射线BC上，EF⊥AD于G，交AB、AC于点F、H，GM⊥BC于M．下列结论：①∠DGM＝∠E；②2∠ADE＝∠ACE+∠B；③∠DAC＝∠EGM﹣∠B；④∠E＝∠ACB﹣∠B．其中正确的结论个数为（　　）

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

11. 点A（4，﹣2）到x轴的距离是．

查看试题解析
12. $27$ 的立方根是．

查看试题解析
13. 如图，已知OA＝OB ， BC⊥AC于点C ，点C对应的数是－2，AC＝1，那么数轴上点B所表示的数是

查看试题解析
14. 如图，已知函数y＝2x+b与函数y＝kx﹣3的图象交于点P，则方程组 ${\begin{array}{l} 2 x - y = - b \\ k x - y = 3 \end{array}$ 的解是.

查看试题解析
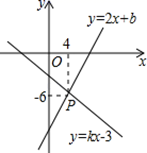15. 已知一组数据x₁ ， x₂ ， x₃ ， x₄ ， x₅的平均数是4，那么另一组数据3x₁﹣2，3x₂﹣2，3x₃﹣2，3x₄﹣2，3x₅﹣2的平均数是．

查看试题解析
16. 若a是 $\sqrt{7}$ 的整数部分，b是它的小数部分，则a﹣b＝．

查看试题解析
17. 如图，直线y＝﹣2x+2与x轴和y轴分别交与A、B两点，射线AP⊥AB于点A若点C是射线AP上的一个动点，点D是x轴上的一个动点，且以C、D、A为顶点的三角线与△AOB全等，则OD的长为．

查看试题解析

三、解答题

18. 计算： $(\sqrt{7} + 2) (\sqrt{7} - 2) - \sqrt{\frac{1}{3}} \times \sqrt{18} + \sqrt{6} - (π - 3)^{0}$

查看试题解析
19. 如图，在直角坐标系中，A（﹣1，5），B（﹣3，0），C（﹣4，3）．

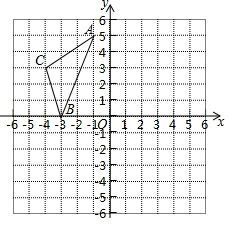(1)、在图中作出△ABC关于y轴对称的图形△A₁B₁C₁；

(2)、写出点A₁ ， B₁ ， C₁的坐标；

(3)、求△ABC的面积．

查看试题解析
20. 如图，在△ABC中，D是BC上一点，AD=BD，∠C=∠ADC，∠BAC=57°，求∠DAC的度数．

查看试题解析
21. 某初中学校欲向高一级学校推荐一名学生，根据规定的推荐程序：首先由本年级200名学生民主投票，每人只能推荐一人（不设弃权票），选出了票数最多的甲、乙、丙三人.投票结果统计如图一：
测试项目
测试成绩/分
甲
乙
丙
笔试
92
90
95
面试
85
95
80
其次，对三名候选人进行了笔试和面试两项测试.各项成绩如右表所示：图二是某同学根据上表绘制的一个不完整的条形图.请你根据以上信息解答下列问题：

(1)、补全图一和图二.

(2)、请计算每名候选人的得票数.

(3)、若每名候选人得一票记1分，投票、笔试、面试三项得分按照2：5：3的比确定，计算三名候选人的平均成绩，成绩高的将被录取，应该录取谁？

查看试题解析
22. 如图，△ACB和△ECD都是等腰直角三角形，CA＝CB，CE＝CD，△ACB的顶点A在△ECD的斜边DE上.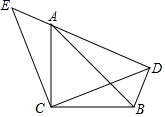

(1)、求证：∠ADB＝90°；

(2)、若AE＝2，AD＝4，求AC.

查看试题解析
23. 进入12月以来某些海鱼的价格逐渐上涨，某农贸市场水产商户老王只好在进货数量上做些调整。12月份前两周两种海鱼的价格情况如下表：

鲅鱼价格

带鱼价格

第一周

8元/千克

18元/千克

第二周

10元/千克

20元/千克

(1)、老王第一周购进了一批鲅鱼和带鱼，总货款是1700元，若按第二周的价格购进与上周相同数量的鲅鱼和带鱼，则需多花300元，求老王第一周购进鲅鱼和带鱼分别是多少千克；

(2)、若第二周将这两种鱼的进货总量减少到120千克，设购进鲅鱼a千克，需要支付的货款为w元，则w与a的函数关系式为；

(3)、在(2)的条件下，若购进鲅鱼不超过80千克，则第二周老王购进这两种鱼的总货款最少应是多少元？

查看试题解析
24. 如图，过点A的两条直线l₁ ， l₂分别与y轴交于点B，C，其中点B在原点上方，点C在原点下方，已知AB＝ $\sqrt{13}$ ， B（0，3）．

(1)、求点A的坐标；

(2)、若△ABC的面积为4，求直线l₂的表达式．

(3)、在（2）的条件下，在直线l₁上是否存在点M，使得△OAM的面积与△OCA的面积相等？若存在，求出M点的坐标；若不存在，请说明理由．

查看试题解析
25. 如图，以Rt△AOC的直角顶点O为原点，以OC、OA所在直线为x轴和y轴建立平面直角坐标系，点A（0，a），C（b，0）满足 $\sqrt{a - 2 b}$ +|b﹣2|＝0．

(1)、C点的坐标为， A点的坐标为；

(2)、如图1，已知坐标轴上有两动点P、Q同时出发，点P从点C出发，沿x轴负方向以1个单位长度每秒的速度匀速移动，点Q从点O出发以2个单位长度每秒的速度沿y轴正方向移动，点Q到达A点整个运动随之结束．AC的中点D的坐标是（1，2），设运动时间为t（t＞0）秒．问：是否存在这样的t，使S_△ODP＝S_△ODQ？若存在，请求出t的值；若不存在，请说明理由；

(3)、如图2，过点O作OG∥AC，作∠AOF＝∠AOG交AC于点F，点E是线段OA上一动点，连接CE交OF于点H，当点E在线段OA上运动的过程中， $\frac{∠ O H C + ∠ A C E}{∠ O E C}$ 的值是否会发生变化？若不变，请求出它的值；若变化，请说明理由，

查看试题解析

区县	大兴	通州	平谷	顺义	怀柔	门头沟	延庆	昌平	密云	房山
最高气温	32	32	30	32	30	32	29	32	30	32

测试项目	测试成绩/分
测试项目	甲	乙	丙
笔试	92	90	95
面试	85	95	80

	鲅鱼价格	带鱼价格
第一周	8元/千克	18元/千克
第二周	10元/千克	20元/千克