广东省揭阳市揭东区2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-07-07 类型：期末考试

进入出卷网下载

一、单选题

1. 下列一组数：﹣8、 $\frac{2}{7}$ 、 $\frac{π}{2}$ 、3.14、0.1010010001…（相邻两个1之间依次增加1个0），其中无理数的个数为（　　）

A、0 B、1 C、2 D、3

查看试题解析
2. 下列选项中不是勾股数的是（　　）

A、7，24，25 B、4，5，6 C、3，4，5 D、9，12，15

查看试题解析
3. 在平面直角坐标系中，下列各点在第四象限的是（）

A、（﹣2，3） B、（2，0） C、（0，﹣3） D、（3，﹣5）

查看试题解析
4. 估算 $\sqrt{2}$ ﹣2的值在（　　　）

A、﹣1到0之间 B、0到1之间 C、1到2之间 D、2到3之间

查看试题解析
5. 若点 $M (a ， - 3) ， N (- 7 ， b)$ 关于 $x$ 轴对称，则 $a 、 b$ 的值分别为（）

A、 $- 7$ ，3 B、 $- 7 ， - 3$ C、7，3 D、7， $- 3$

查看试题解析
6. 下列命题是假命题的是（）．

A、 $\sqrt{10}$ 是最简二次根式 B、若点A（-2，a），B（3，b）在直线y=-2x+1，则a>b C、数轴上的点与有理数一一对应 D、点A（2，5）关于y轴的对称点的坐标是（-2，5）

查看试题解析
7. 古希腊几何学家海伦和我国宋代数学家秦九韶都曾提出利用三角形的三边求面积的公式，称为海伦﹣秦九韶公式：如果一个三角形的三边长分别是 $a$ ， $b$ ， $c$ ，记 $p = \frac{a + b + c}{2}$ ，那么三角形的面积为 $S = \sqrt{p (p - a) (p - b) (p - c)}$ .如图，在 $△ A B C$ 中， $∠ A$ ， $∠ B$ ， $∠ C$ 所对的边分别记为 $a$ ， $b$ ， $c$ ，若 $a = 5$ ， $b = 7$ ， $c = 8$ ，则 $△ A B C$ 的面积为（）

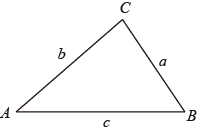A、14 B、20 C、 $10 \sqrt{3}$ D、 $10 \sqrt{6}$

查看试题解析
8. 20位同学在植树节这天共种了52棵树苗，其中男生每人种3棵，女生每人种2棵．设男生有x人，女生有y人，根据题意，列方程组正确的是（　　）

A、 $\{\begin{matrix} x + y = 52 \\ 3 x + 2 y = 20 \end{matrix}$ B、 $\{\begin{matrix} x + y = 52 \\ 2 x + 3 y = 20 \end{matrix}$ C、 $\{\begin{matrix} x + y = 20 \\ 2 x + 3 y = 52 \end{matrix}$ D、 $\{\begin{matrix} x + y = 20 \\ 3 x + 2 y = 52 \end{matrix}$

查看试题解析
9. 某商场销售A ， B ， C ， D四种商品，它们的单价依次是50元，30元，20元，10元．某天这四种商品销售数量的百分比如图所示，则这天销售的四种商品的平均单价是（）

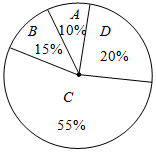A、19.5元 B、21.5元 C、22.5元 D、27.5元

查看试题解析
10. 如图，直线y＝ $\frac{\sqrt{3}}{3}$ x，点A₁坐标为（1，0），过点A₁作x轴的垂线交直线于点B₁ ，以原点O为圆心，OB₁长为半径画弧x轴于点A₂；再过点A₂作x轴的垂线交直线于点B₂ ，以原点O为圆心，OB₂长为半径画弧交x轴于点A₃ ， ……，按此做法进行下去，点An的横坐标为（　　）

A、 $(\frac{2 \sqrt{3}}{3})^{n - 1}$ B、 $(\frac{2 \sqrt{3}}{3})^{n}$ C、2 $(\frac{\sqrt{3}}{3})^{n}$ D、2 $(\frac{\sqrt{3}}{3})^{n - 1}$

查看试题解析

二、填空题

11. 0.81的算术平方根是．

查看试题解析
12. 直线y=3x-2不经过第象限.

查看试题解析
13. 某班7个兴趣小组的人数如下：5，6，6，x，7，8，9，已知这组数据的平均数为7，则这组数据的中位数是.

查看试题解析
14. 如图，一副三角板AOC和BCD如图摆放，则∠BOC的度数为°．

查看试题解析
15. 如图，直线 $l_{1}$ ： $y = x + 2$ 与直线 $l_{2}$ ： $y = k x + b$ 相交于点P（m，4），则方程组 ${\begin{matrix} y = x + 2 \\ y = k x + b \end{matrix}$ 的解是．

查看试题解析
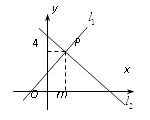16. 如图，在圆柱的截面ABCD中，AB＝ $\frac{16}{π}$ ，BC＝12，动点P从A点出发，沿着圆柱的侧面移动到BC的中点S的最短距离为.

查看试题解析
17. 如图：在平面直角坐标系中，已知正比例函数 $y = \frac{3}{4} x$ 与一次函数 $y = - 2 x + 11$ 的图象交于点A，设x轴上有一点P作x轴的垂线（垂足位于点A的右侧），分别交 $y = \frac{3}{4} x$ 和 $y = - 2 x + 11$ 的图象于点B、C，连接OC，若 $B C = \frac{11}{5} O A$ ，则△OBC的面积为．

查看试题解析

三、解答题

18. 计算： $- 1^{2020} + \sqrt{25} + \sqrt[3]{- 8} + | 2 - \sqrt{5} |$ ．

查看试题解析
19. 解二元一次方程组： ${\begin{matrix} 4 x - 2 y + 5 = 0 \\ 9 x + 3 y = 0 \end{matrix}$ ．

查看试题解析
20. 如图，在直角坐标系中，△ABC的三个顶点坐标分别为A（1，4），B（4，2），C（3，5），请回答下列问题：

(1)、作出△ABC关于x轴的对称图形△A₁B₁C₁ ，并直接写出△A₁B₁C₁的顶点坐标．

(2)、求△A₁B₁C₁的面积．

查看试题解析
21. 某校在八年级开展环保知识问卷调查活动，问卷一共10道题，每题10分，八年级（三）班的问卷得分情况统计图如下图所示：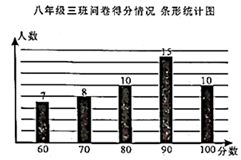

(1)、扇形统计图中，a的值为．

(2)、根据以上统计图中的信息，求这问卷得分的众数和中位数分别是多少分？

(3)、已知该校八年级共有学生600人，请估计问卷得分在80分以上（含80分）的学生约有多少人？

查看试题解析
22. 如图，已知等腰△ABC的底边BC＝13，D是腰AB上一点，且CD＝12，BD＝5．

(1)、求证：△BDC是直角三角形；

(2)、求AC的长．

查看试题解析
23. 疫情期间为保护学生和教师的健康，某学校储备“抗疫物资”用29000元购进甲、乙两种医用口罩共计900盒，甲，乙两种口罩的售价分别是30元/盒，35元/盒．

(1)、求甲、乙两种口罩各购进了多少盒？

(2)、现已知甲，乙两种口罩的数量分别是20个/盒，25个/盒，按照市教育局要求，学校必须储备足够使用10天的口罩，该校师生共计900人，每人每天2个口罩，问购买的口罩数量是否能满足市教育局的要求？

查看试题解析
24. 已知一次函数y＝﹣ $\frac{1}{2}$ x+b的图象与y轴交于点A，与x轴交于点B，与正比例函数y＝2x的图象交于点C（1，a）．

(1)、求a，b的值；

(2)、方程组 ${\begin{array}{l} 2 x - y = 0 \\ \frac{1}{2} x + y = b \end{array}$ 的解为　　．

(3)、在y＝2x的图象上是否存在点P，使得△BOP的面积比△AOP的面积大5？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由．

查看试题解析
25. 已知：如图所示，直线MN∥GH，另一直线交GH于A，交MN于B，且∠MBA＝80°，点C为直线GH上一动点，点D为直线MN上一动点，且∠GCD＝50°．

(1)、如图1，当点C在点A右边且点D在点B左边时，∠DBA的平分线交∠DCA的平分线于点P，求∠BPC的度数；

(2)、如图2，当点C在点A右边且点D在点B右边时，∠DBA的平分线交∠DCA的平分线于点P，求∠BPC的度数；

(3)、当点C在点A左边且点D在点B左边时，∠DBA的平分线交∠DCA的平分线所在直线交于点P，请直接写出∠BPC的度数，不说明理由．

查看试题解析