广东省惠州市惠城区2020-2021学年八年级上学期期末数学试题
试卷更新日期:2022-07-07 类型:期末考试
一、单选题
-
1. 下列图形中有稳定性的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若 , 则a的取值正确的是( )A、 B、 C、 D、3. 下列运算中,正确的是( )A、 B、 C、 D、4. 如图,在中,是的平分线, , 垂足为E.若 , 则的长为( )
2. 若 , 则a的取值正确的是( )A、 B、 C、 D、3. 下列运算中,正确的是( )A、 B、 C、 D、4. 如图,在中,是的平分线, , 垂足为E.若 , 则的长为( )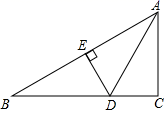 A、 B、 C、 D、5. 一个n边形的各内角都等于 , 则n等于( )A、5 B、6 C、7 D、86. 将一副直角三角板按如图所示的位置摆放,使得它们的直角边互相垂直,则 的度数是( )
A、 B、 C、 D、5. 一个n边形的各内角都等于 , 则n等于( )A、5 B、6 C、7 D、86. 将一副直角三角板按如图所示的位置摆放,使得它们的直角边互相垂直,则 的度数是( )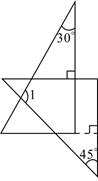 A、 B、 C、 D、7. 在边长为a的正方形中剪掉一个边长为b的正方形[ , 如图(1)],然后将剩余部分拼成一个长方形[如图(2)].上述操作能验证的等式是( )
A、 B、 C、 D、7. 在边长为a的正方形中剪掉一个边长为b的正方形[ , 如图(1)],然后将剩余部分拼成一个长方形[如图(2)].上述操作能验证的等式是( ) A、 B、 C、 D、8. 若x2+mx+1是完全平方式,则m等于( )A、2 B、-2 C、±2 D、±49. 下面的计算过程中,从哪一步开始出现不符合题意( ).
A、 B、 C、 D、8. 若x2+mx+1是完全平方式,则m等于( )A、2 B、-2 C、±2 D、±49. 下面的计算过程中,从哪一步开始出现不符合题意( ). A、① B、② C、③ D、④10. 如图,将一张三角形纸片 的一角折叠,使点 落在 处的 处,折痕为 .如果 , , ,那么下列式子中正确的是( )
A、① B、② C、③ D、④10. 如图,将一张三角形纸片 的一角折叠,使点 落在 处的 处,折痕为 .如果 , , ,那么下列式子中正确的是( )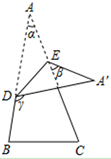 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 五边形的外角和是度.12. 若 , 则x-y= .13. 计算: .14. 化简 .15.
如图,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则∠ABC+∠DFE= 度.
 16.
16.在一自助夏令营活动中,小明同学从营地A出发,要到A地的北偏东60°方向的C处,他先沿正东方向走了200m到达B地,再沿北偏东30°方向走,恰能到达目的地C(如图),那么,由此可知,B、C两地相距 m.
 17. 如图,等腰三角形的底边长为4,面积是16,腰的垂直平分线分别交 , 边于E,F点若点D为边的中点,点M为线段上动点,则周长的最小值为 .
17. 如图,等腰三角形的底边长为4,面积是16,腰的垂直平分线分别交 , 边于E,F点若点D为边的中点,点M为线段上动点,则周长的最小值为 .
三、解答题
-
18. 分解因式: .19. 如图,点B,C,E,F在同一直线上, , , , 垂足分别为C,F, . 求证: .
 20. 某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需时间与原计划生产450机器所需时间相同,求该工厂原来平均每天生产多少台机器?21. 已知实数a,b满足 , 求的值.22. 如图,在中, , D为中点,平分交于点E,过点E作交于点F.
20. 某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需时间与原计划生产450机器所需时间相同,求该工厂原来平均每天生产多少台机器?21. 已知实数a,b满足 , 求的值.22. 如图,在中, , D为中点,平分交于点E,过点E作交于点F.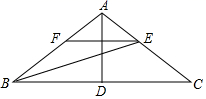 (1)、若 , 求的度数;(2)、求证: .
(1)、若 , 求的度数;(2)、求证: .

