广东省惠州市2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-07-07 类型:期末考试
一、单选题
-
1. 下列图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列长度的三条线段可以组成三角形的是( )A、3,4,8 B、5,6,11 C、1,2,3 D、5,6,103. 若分式 的值为零,则x=( )A、3 B、-3 C、±3 D、04. 如图,已知 , ,增加哪个条件不能保证 的是( )
2. 下列长度的三条线段可以组成三角形的是( )A、3,4,8 B、5,6,11 C、1,2,3 D、5,6,103. 若分式 的值为零,则x=( )A、3 B、-3 C、±3 D、04. 如图,已知 , ,增加哪个条件不能保证 的是( ) A、 B、 C、 D、5. 在直角坐标系中,点 与点 关于 轴对称,则点 的坐标为( )A、 B、 C、 D、6. 下列等式成立的是( )A、 B、 C、 D、7. 如图所示,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下列结论中错误的是( )
A、 B、 C、 D、5. 在直角坐标系中,点 与点 关于 轴对称,则点 的坐标为( )A、 B、 C、 D、6. 下列等式成立的是( )A、 B、 C、 D、7. 如图所示,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下列结论中错误的是( )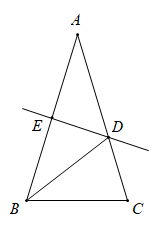 A、BD平分∠ABC B、△BCD的周长等于AB+BC C、AD=BD=BC D、△BCD的面积等于△BED的面积8. 等腰三角形的一边长等于4,一边长等于9,则它的周长是( )A、17 B、22 C、17或22 D、139. 根据图①的面积可以说明多项式的乘法运算(2a+b)(a+b)=2a2+3ab+b2 , 那么根据图②的面积可以说明多项式的乘法运算是( )
A、BD平分∠ABC B、△BCD的周长等于AB+BC C、AD=BD=BC D、△BCD的面积等于△BED的面积8. 等腰三角形的一边长等于4,一边长等于9,则它的周长是( )A、17 B、22 C、17或22 D、139. 根据图①的面积可以说明多项式的乘法运算(2a+b)(a+b)=2a2+3ab+b2 , 那么根据图②的面积可以说明多项式的乘法运算是( ) A、(a+3b)(a+b)=a2+4ab+3b2 B、(a+3b)(a+b)=a2+3b2 C、(b+3a)(b+a)=b2+4ab+3a2 D、(a+3b)(a﹣b)=a2+2ab﹣3b210. 如图,已知 和 都是等腰三角形, , 交于点F,连接 ,下列结论:① ;② ;③ 平分 ;④ .其中正确结论的个数有( )
A、(a+3b)(a+b)=a2+4ab+3b2 B、(a+3b)(a+b)=a2+3b2 C、(b+3a)(b+a)=b2+4ab+3a2 D、(a+3b)(a﹣b)=a2+2ab﹣3b210. 如图,已知 和 都是等腰三角形, , 交于点F,连接 ,下列结论:① ;② ;③ 平分 ;④ .其中正确结论的个数有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 计算: .12. 分解因式:a3-a=13. 如图,AB=AC,BD=BC,若∠A=40°,则∠ABD的度数是.
 14. 如图,等腰三角形ABC的底边BC长为4,面积是12,腰AB的垂直平分线EF分别交AB,AC于点E、F,若点D为底边BC的中点,点M为线段EF上一动点,则△BDM的周长的最小值为 .
14. 如图,等腰三角形ABC的底边BC长为4,面积是12,腰AB的垂直平分线EF分别交AB,AC于点E、F,若点D为底边BC的中点,点M为线段EF上一动点,则△BDM的周长的最小值为 .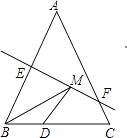 15. 如图, 中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E,且AB=10cm,则 的周长是cm.
15. 如图, 中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E,且AB=10cm,则 的周长是cm. 16. 已知:x2-8x-3=0,则(x-1)(x-3)(x-5)(x-7)的值是。17. 已知关于x的分式方程 有一个正数解,则k的取值范围为.
16. 已知:x2-8x-3=0,则(x-1)(x-3)(x-5)(x-7)的值是。17. 已知关于x的分式方程 有一个正数解,则k的取值范围为.三、解答题
-
18. 计算:19. 如图:AE=DE,BE=CE,AC和BD相交于点E,求证:AB=DC
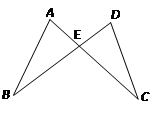 20. 解方程: .21. 先化简,再求值:(x+1)÷(2+ ),其中x=﹣ .22. 如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣3),C(﹣1,﹣1).
20. 解方程: .21. 先化简,再求值:(x+1)÷(2+ ),其中x=﹣ .22. 如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣3),C(﹣1,﹣1).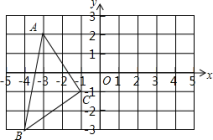
⑴在图中作出关于y轴对称的;
⑵写出点的坐标(直接写答案);
⑶在y轴上画出点P,使PB+PC最小.
23. 某地为某校师生交通方便,在通往该学校原道路的一段全长为300 m的旧路上进行整修铺设柏油路面.铺设120 m后,为了尽量减少施工对城市交通所造成的影响,后来每天的工效比原计划增加20%,结果共用30天完成这一任务.(1)、求原计划每天铺设路面的长度;(2)、若市政部门原来每天支付工人工资为600元,提高工效后每天支付给工人的工资增长了30%,现市政部门为完成整个工程准备了25 000元的流动资金.请问,所准备的流动资金是否够支付工人工资?并说明理由.24. 阅读材料:把形的二次三项式(或其一部分)配成完全平方式的方法叫配方法.配方法的基本形式是完全平方公式的逆写,即 . 请根据阅读材料解决下列问题:(1)、填空: .(2)、先化简,再求值: , 其中满足 .(3)、若分别是的三边,且 , 试判断的形状,并说明理由.25. 如图①,直线AB与x轴负半轴、y轴正半轴分别交于A、B两点,OA、OB的长度分别为a和b,且满足a2﹣2ab+b2=0.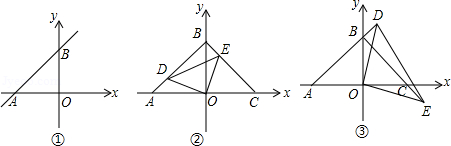 (1)、判断△AOB的形状;(2)、如图②,△COB和△AOB关于y轴对称,D点在AB上,点E在BC上,且AD=BE,试问:线段OD、OE是否存在某种确定的数量关系和位置关系?写出你的结论并证明;(3)、将(2)中∠DOE绕点O旋转,使D、E分别落在AB,BC延长线上(如图③),∠BDE与∠COE有何关系?直接说出结论,不必说明理由.
(1)、判断△AOB的形状;(2)、如图②,△COB和△AOB关于y轴对称,D点在AB上,点E在BC上,且AD=BE,试问:线段OD、OE是否存在某种确定的数量关系和位置关系?写出你的结论并证明;(3)、将(2)中∠DOE绕点O旋转,使D、E分别落在AB,BC延长线上(如图③),∠BDE与∠COE有何关系?直接说出结论,不必说明理由.