广东省广州市天河区2021-2022学年八年级上学期期末数学试题
试卷更新日期：2022-07-07 类型：期末考试
一、单选题
-
1. 下列选项是科学防控知识的图片，图片上有图案和文字说明，其中的图案是轴对称图形的是（ ）A、
打喷嚏捂鼻子
B、
喷嚏后慎揉眼
C、
戴口罩讲卫生
D、
勤洗手勤通风
2. 要使分式有意义，则x的取值范围为（ ）A、x≠﹣2 B、x＝2 C、x＝﹣2 D、x≠03. 已知三角形的两边长分别为3cm和4cm，则该三角形第三边的长不可能是（ ）A、2cm B、3cm C、5cm D、7cm4. 科学家发现一种病毒直径为0.00023微米，则0.00023用科学记数法可以表示为（ ）A、2.3×104 B、0.23×10﹣3 C、2.3×10﹣4 D、23×10﹣55. 若一个正多边形的各个内角都是140°，则这个正多边形是（ ）A、正七边形 B、正八边形 C、正九边形 D、正十边形6. 下列计算正确的是（ ）A、a+a2＝a3 B、a6÷a3＝a3 C、（﹣a2b）3＝a6b3 D、（a+2）2＝a2+47. 如图， 与 相交于 ，且 ，如果添加一个条件还不能判定 ≌ ，则添加的这个条件是（ ）
A、 B、 C、 D、8. 若（x-m）（x+1）的运算结果中不含x的一次项，则m的值等于（ ）A、0 B、1 C、2 D、39.如图所示的正方形网格中，网格线的交点称为格点．已知A、B是两格点，如果C也是图中的格点，且使得△ABC为等腰三角形，则点C的个数是（ ）
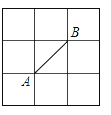A、6 B、7 C、8 D、910. △ABC中，AB＝AC，∠A＝36°，若按如图的尺规作图方法作出线段BD，则下列结论错误的是（ ）
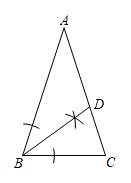A、AD＝BD B、∠BDC＝72° C、S△ABD：S△BCD＝BC：AC D、△BCD的周长＝AB+BC二、填空题
-
11. 因式分解： ．12. 如图，∠ACD是△ABC的外角，若∠ACD＝120°，∠A＝50°，则∠B＝ ．
13. 如图，在△ABC中，AB=AC，AD⊥BC，垂足为D，若BC=4，则BD= ．
14. 若x+y＝3，且xy＝1，则代数式x2+y2的值为 ．15. 如图，B处在A处的南偏西40°方向，C处在A处的南偏东15°方向， C处在B处的北偏东80°方向，则∠ACB＝ ．
16. 在△ABC中，AD是BC边上的中线，△ADC的周长比△ABD的周长多3cm，已知AB＝4cm，则AC的长为 ．三、解答题
-
17. 计算：18. 如图，AC和BD相交于点O，OA=OC，DC∥AB．求证DC=AB．
19. 如图，在平面直角坐标系中，图中的小方格都是边长为1的正方形，△ABC各顶点坐标分别为A(4，0)，B(-1，4)，C(-3，1)，已知点D与点B关于x轴对称，请在方格中找出点D，并求出△ABD的面积．
20. 化简 ， 并在0，1，2中选一个合适的数作为x的值代入求值．21. 如图，△ABC中，∠C＝90°．
(1)、尺规作图：作边BC的垂直平分线，与边BC，AB分别交于点D和点E；（保留作图痕迹，不要求写作法）(2)、若点E是边AB的中点，AC＝BE，求证：△ACE是等边三角形．22. 截至2021年9月，广州已累计建成5G基站超5.2万座，据广州市工信局介绍，广州要打造5G应用示范城市，到2023年5G个人普及率将超过60%.5G是第5代移动通信技术的简称，经测试5G下载速度是4G下载速度的15倍，小英和小芳分别用5G与4G下载一部900兆的纪录片，小英比小芳所用的时间快210秒，求该地4G与5G的下载速度．23. 如图，CD是△ABC的角平分线，DE，DF分别是△ACD和△BCD的高．
(1)、求证CD⊥EF；(2)、若AC＝6，BC＝4，S△ABC＝10，∠ACB＝60°，求CG的长．24. 阅读：因为（x+3）（x-2）=x2+x-6，说明x2+x-6有一个因式是x-2；当因式x-2=0，那么多项式x2+x-6的值也为0，利用上面的结果求解：(1)、多项式A有一个因式为x+m（m为常数），当x= ， A=0；(2)、长方形的长和宽都是整式，其中一条边长为x-2，面积为x2+kx-14，求k的值；(3)、若有一个长方体容器的长为（x+2），宽为（x-1），体积为4x3+ax2-7x+b，试求a，b的值．25. △ABC是等边三角形，点D是AC边上动点，∠CBD＝α（0°＜α＜30°），把△ABD沿BD对折，得到△A′BD．
(1)、如图1，若α＝15°，则∠CBA′＝ ．(2)、如图2，点P在BD延长线上，且∠DAP＝∠DBC＝α．①试探究AP，BP，CP之间是否存在一定数量关系，猜想并说明理由．
②若BP＝10，CP＝m，求CA′的长．（用含m的式子表示）