广东省广州市花都区2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-07-07 类型：期末考试

进入出卷网下载

一、单选题

1. 下列标志图形属于轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 已知在△ABC中，AB＝4，BC＝7，则边AC的长可能是（　　）

A、2 B、3 C、4 D、11

查看试题解析
3. 新型冠状病毒是冠状病毒的一种，该病毒是一种单链RNA病毒，侵入人体后可引起上下呼吸道感染，主要症状为发热、乏力、干咳．新型冠状病毒的直径平均约为100纳米，合约0.0000001米，用科学记数法表示0.0000001米为（　　）

A、﹣1×10⁶米 B、﹣1×10⁷米 C、1×10^﹣⁶米 D、1×10^﹣⁷米

查看试题解析
4. 已知图中的两个三角形全等，图中的字母表示三角形的边长，则∠1等于（）

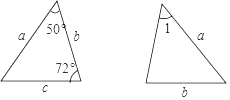A、72° B、60° C、50° D、58°

查看试题解析
5. 下列运算中，正确的是（　　）

A、3x³+2x²＝5x² B、a•a²＝a³ C、3a⁶÷a³＝3a² D、（ab）³＝a³b

查看试题解析
6. 计算（2x+1）（x﹣5）的结果是（　　）

A、2x²﹣9x﹣5 B、2x²﹣9x+5 C、2x²﹣11x﹣5 D、2x²﹣11x+5

查看试题解析
7. 一个凸多边形的内角和与外角和之比为2：1，则这个多边形的边数为（　　）

A、5 B、6 C、7 D、8

查看试题解析
8. 如图，在△ABC中，∠B＝90°，AD平分∠BAC，交BC于点D，BC＝8cm，BD：CD＝3：4，则点D到AC的距离为（　　）cm．

A、3 B、4 C、 $\frac{32}{7}$ D、 $\frac{24}{7}$

查看试题解析
9. 剪纸艺术是最古老的中国民间艺术之一，很多剪纸作品体现了数学中的对称美．如图，蝴蝶剪纸是一幅轴对称图形，将其放在平面直角坐标系中，如果图中点E的坐标为（2m，﹣n），其关于y轴对称的点F的坐标（3﹣n，﹣m+1），则（m﹣n）²⁰²²的值为（　　）

A、3²⁰²² B、﹣1 C、1 D、0

查看试题解析
10. 如图，点E在等边△ABC的边BC上，BE＝4，射线CD⊥BC，垂足为点C，点P是射线CD上一动点，点F是线段AB上一动点，当EP+FP的值最小时，BF＝5，则AB的长为（　　）

A、7 B、8 C、9 D、10

查看试题解析

二、填空题

11. 若分式 $\frac{2}{x - 3}$ 有意义，则 $x$ 应满足的条件是.

查看试题解析
12. 计算 $(\sqrt{3} - π)^{0} + 2^{- 2}$ ＝．

查看试题解析
13. 如图，已知∠1＝∠2，要判定△ABD≌△ACD，请你添加一个条件是．（写出一个即可）

查看试题解析
14. 如图，在△ABC中，AD、AE分别是BC边上的中线和高，AE＝6，S_△ABD＝15，则CD＝．

查看试题解析
15. 已知一个等腰三角形一腰与另一腰上高夹角为20°，则这个等腰三角形的顶角为 °．

查看试题解析
16. 如图，在四边形ABCD中，AB＝BC，AD＝CD，我们把这种两组邻边分别相等的四边形叫做“筝形”．筝形ABCD的对角线AC、BD相交于点O．已知∠ADC＝120°，∠ABC＝60°，小婵同学得到如下结论：①△ABC是等边三角形；②BD＝2AD；③S_四_边_形ABCD＝AC•BD；④点M、N分别在线段AB、BC上，且∠MDN＝60°，则MN＝AM+CN，其中正确的结论有．（填写所有正确结论的序号）

查看试题解析

三、解答题

17. 解方程： $\frac{3}{x - 3} = \frac{2}{x}$ ．

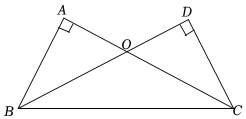
查看试题解析
18. 因式分解：ab²﹣4a．

查看试题解析
19. 如图，AB⊥AC，CD⊥BD，AB＝DC，AC与BD交于点O．求证：OB＝OC．

查看试题解析
20. 如图，在Rt△ABC中，∠BAC＝60°，AD、BE分别是∠BAC与∠ABC的平分线，并交于点H．

(1)、若DC＝2，则AD＝；

(2)、∠AHB的度数．

查看试题解析
21. 已知： $A = \frac{a^{2} + 2 a + 1}{a^{2} - 1} - \frac{a}{a - 1}$ ．

(1)、化简A；

(2)、当a³＝8时，求A的值．

查看试题解析
22. 我们定义：顶角等于36°的等腰三角形为黄金三角形．如图，△ABC中，AB＝AC且∠A＝36°，则△ABC为黄金三角形．

(1)、尺规作图：作∠B的角平分线，交AC于点D．（保留作图痕迹，不写作法）．

(2)、请判断△BDC是否为黄金三角形，如果是，请给出证明，如果不是，请说明理由．

查看试题解析
23. 某校推行“新时代好少年•红心向党”主题教育读书工程建设活动，原计划投资10000元建设几间青少年党史“读书吧”，为了保证“读书吧”的建设的质量，实际每间“读书吧”的建设费用增加了10%，实际总投资为15400元，并比原计划多建设了2间党史“读书吧”.

(1)、原计划每间党史“读书吧”的建设费用是多少元？

(2)、该校实际共建设了多少间青少年党史“读书吧”？

查看试题解析
24. 如图1，有A型、B型、C型三种不同形状的纸板，A型是边长为a的正方形，B型是边长为b的正方形，C型是长为b，宽为a的长方形．现用A型纸板一张，B型纸板一张，C型纸板两张拼成如图2的大正方形．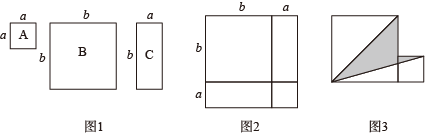

(1)、观察图2，请你用两种方法表示出图2的总面积．
方法1：；方法2：；

请利用图2的面积表示方法，写出一个关于a，b的等式：．

(2)、已知图2的总面积为49，一张A型纸板和一张B型纸板的面积之和为25，求ab的值．

(3)、用一张A型纸板和一张B型纸板，拼成图3所示的图形，若a+b＝8，ab＝15，求图3中阴影部分的面积．

查看试题解析
25. 如图，∠ACD是等边△ABC的一个外角，点E是∠ACD内部任意一点，作直线CE．

(1)、当CE平分∠ACD时，证明：AB∥CE．

(2)、已知点A关于直线CE的对称点为F，连接AF、BF、CF，其中AF、BF分别交直线CE于P、Q两点．记∠ACE＝α，当0＜α＜60°时，求∠BFC，（用含α的式子表示）

(3)、若（2）中的α满足0°＜α＜120°时，
①∠AFB＝　　°；
②探究线段QB、QC、QP之间的数量关系，并证明．

查看试题解析