广东省广州市海珠区2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-07-07 类型:期末考试
一、单选题
-
1. 要使分式 有意义,则x的取值范围是( )A、x≠1 B、x>1 C、x<1 D、x≠﹣12. 用科学记数法表示的数﹣5.6×10﹣4写成小数是( )A、﹣0.00056 B、﹣0.0056 C、﹣56000 D、0.000563. 已知一个正多边形的每个外角等于45°,则这个正多边形是( )A、正五边形 B、正六边形 C、正七边形 D、正八边形4. 下列从左到右的变形属于因式分解的是( )A、x2+2x+1=x(x+2)+1 B、﹣7ab2c3=﹣abc•7bc2 C、m(m+3)=m2+3m D、2x2﹣5x=x(2x﹣5)5. 如图,已知∠1=∠2,要得到结论ABC≌ADC,不能添加的条件是( )
 A、BC=DC B、∠ACB=∠ACD C、AB=AD D、∠B=∠D6. 已知2x=5,则2x+3的值是( )A、8 B、15 C、40 D、1257. 若mx+6y与x﹣3y的乘积中不含有xy项,则m的值为( )A、0 B、2 C、3 D、68. 如图,ABC中,AB>AC,AD平分∠BAC,AE⊥BC于E,若∠B=α,∠C=β,则∠ADC的度数为( )
A、BC=DC B、∠ACB=∠ACD C、AB=AD D、∠B=∠D6. 已知2x=5,则2x+3的值是( )A、8 B、15 C、40 D、1257. 若mx+6y与x﹣3y的乘积中不含有xy项,则m的值为( )A、0 B、2 C、3 D、68. 如图,ABC中,AB>AC,AD平分∠BAC,AE⊥BC于E,若∠B=α,∠C=β,则∠ADC的度数为( ) A、 B、 C、 D、9. 如图,△ABC≌△ADE,点D在BC上,且∠B=60°,则∠EDC的度数等于( )
A、 B、 C、 D、9. 如图,△ABC≌△ADE,点D在BC上,且∠B=60°,则∠EDC的度数等于( ) A、30° B、45° C、60° D、75°10. 如图,∠A+∠B+∠C+∠D+∠E+∠F的值是( )
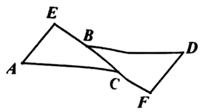
A、30° B、45° C、60° D、75°10. 如图,∠A+∠B+∠C+∠D+∠E+∠F的值是( )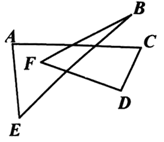 A、240° B、360° C、540° D、720°
A、240° B、360° C、540° D、720°二、填空题
-
11. 计算: .12. 已知点A关于x轴的对称点B的坐标为(1,﹣2),则点A的坐标为 .13. 如图,RtABC中,∠C=90°,D是BC的中点,∠CAD=30°,BC=6,则AD+DB的长为 .
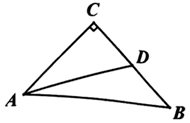 14. 在RtABC中,∠C=90°,若BC=6,AD平分∠BAC交BC于点D,BD=2CD,则点D到线段AB的距离为 .
14. 在RtABC中,∠C=90°,若BC=6,AD平分∠BAC交BC于点D,BD=2CD,则点D到线段AB的距离为 .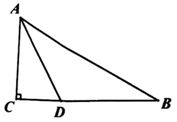 15. 边长分别为m和2m的两个正方形如图的样式摆放,则图中阴影部分的面积为 .
15. 边长分别为m和2m的两个正方形如图的样式摆放,则图中阴影部分的面积为 . 16. 如图,在ABC中,CD是AB边上的中线,设BC=a,AC=b,若a,b满足a2﹣10a+b2﹣18b+106=0,则CD的取值范围是 .
16. 如图,在ABC中,CD是AB边上的中线,设BC=a,AC=b,若a,b满足a2﹣10a+b2﹣18b+106=0,则CD的取值范围是 .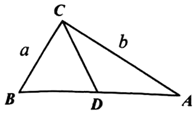
三、解答题
-
17. 计算:(1)、(2)、18. 已知:如图,AEFD,AE=FD,EB=CF.求证: .
 19. 先化简,再求值: , 其中a=2021.20. 列方程解应用题:一批学生志愿者去距学校8km的老人院参加志愿服务活动,一部分学生骑自行车先走,过了15min后,其余学生乘汽车出发,结果他们同时到达.已知骑车学生的速度是汽车速度的一半,求骑车学生的速度.21. 已知:如图,PC平分∠APB,CM⊥PA于M,CN⊥PB于N,D、E分别是边PA和PB上的点,且CD=CE.求证:∠APB+∠DCE=180°.
19. 先化简,再求值: , 其中a=2021.20. 列方程解应用题:一批学生志愿者去距学校8km的老人院参加志愿服务活动,一部分学生骑自行车先走,过了15min后,其余学生乘汽车出发,结果他们同时到达.已知骑车学生的速度是汽车速度的一半,求骑车学生的速度.21. 已知:如图,PC平分∠APB,CM⊥PA于M,CN⊥PB于N,D、E分别是边PA和PB上的点,且CD=CE.求证:∠APB+∠DCE=180°.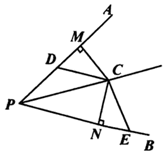 22. 如图,在边长为单位1的小正方形组成的10×10网格中(我们把组成网格的小正方形的顶点称为格点),点A和点B分别在网格的格点上.
22. 如图,在边长为单位1的小正方形组成的10×10网格中(我们把组成网格的小正方形的顶点称为格点),点A和点B分别在网格的格点上.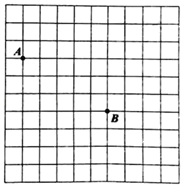 (1)、分解因式2a2﹣18;(2)、若2a2﹣18=0,且点A(a,2)在第二象限,点B(a+5,﹣1)在第四象限,请求出点A和点B的坐标,并在所给的网格中画出平面直角坐标系;(3)、在(2)的条件下,已知点(a,﹣4)是点A关于直线的对称点,点C在直线l上,且ABC的面积为6,直接写出点C的坐标.23. 已知ABC中,∠B=∠C=α.
(1)、分解因式2a2﹣18;(2)、若2a2﹣18=0,且点A(a,2)在第二象限,点B(a+5,﹣1)在第四象限,请求出点A和点B的坐标,并在所给的网格中画出平面直角坐标系;(3)、在(2)的条件下,已知点(a,﹣4)是点A关于直线的对称点,点C在直线l上,且ABC的面积为6,直接写出点C的坐标.23. 已知ABC中,∠B=∠C=α.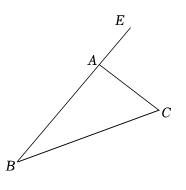 (1)、尺规作图(不要求写作法,但要保留作图痕迹):
(1)、尺规作图(不要求写作法,但要保留作图痕迹):①作∠EAC的平分线AD;
②在AD上作点P,使ACP是以AC为底边的等腰三角形,并求出∠APC的度数(用含α的式子表示);
(2)、在(1)所作的AD上是否存在着另外的点P,使ACP也为等腰三角形,若有,请直接用含α的式子表示∠APC的大小;若没有,请说明理由.24. 阅读材料:对于非零实数a,b,若关于x的分式的值为零,则解得x1=a,x2=b.又因为﹣(a+b),所以关于x的方程x+=a+b的解为x1=a,x2=b.(1)、理解应用:方程的解为:x1= , x2=;(2)、知识迁移:若关于x的方程x+=5的解为x1=a,x2=b,求a2+b2的值;(3)、拓展提升:若关于x的方程=k﹣x的解为x1=t+1,x2=t2+2,求k2﹣4k+2t3的值.25. 已知:如图,ABC中,AB=AC,∠A=45°,E是AC上的一点,∠ABE=∠ABC,过点C作CD⊥AB于D,交BE于点P.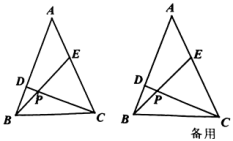 (1)、直接写出图中除ABC外的所有等腰三角形;(2)、求证:BD=PC;(3)、点H、G分别为AC、BC边上的动点,当DHG周长取取小值时,求∠HDG的度数.
(1)、直接写出图中除ABC外的所有等腰三角形;(2)、求证:BD=PC;(3)、点H、G分别为AC、BC边上的动点,当DHG周长取取小值时,求∠HDG的度数.