广东省广州市番禺区2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-07-07 类型：期末考试

进入出卷网下载

一、单选题

1. 如图，将三角形纸板的直角顶点放在直尺的一边上，∠1＝20°，∠3＝30°，则∠2＝（　　）

A、50° B、60° C、30° D、20°

查看试题解析
2. 下列长度的三根木条首尾相连，能组成三角形的是（　　）

A、3，4，8 B、8，7，15 C、2，2，3 D、5，5，11

查看试题解析
3. 下列运算中正确的是（）．

A、 $x^{2} \cdot x^{5} = x^{10}$ B、 ${(- x^{2})}^{4} = - x^{8}$ C、 ${(- x y^{2})}^{2} = x y^{4}$ D、 $x^{5} \div x^{3} = x^{2}$

查看试题解析
4. 若分式 $\frac{x - 1}{x + 2}$ 的值为零，则x的值是(　　)

A、0 B、1 C、 $- 1$ D、 $- 2$

查看试题解析
5. 把一张正方形纸片按如图所示的方法对折两次后剪去两个角，那么打开以后的形状是（）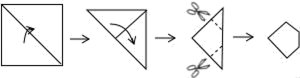

A、六边形 B、八边形 C、十二边形 D、十六边形

查看试题解析
6. 等腰三角形的顶角为80°，则其底角的度数是（　　）

A、100° B、80° C、50° D、40°

查看试题解析
7. 如图， $△ A B C$ 与 $△ A^{'} B^{'} C^{'}$ 关于直线l对称， $∠ A = 50 °$ ， $∠ C^{'} = 30 °$ ，则 $∠ B$ 的度数为（）．

A、30° B、50° C、90° D、100°

查看试题解析
8. 把代数式x²﹣4x+4分解因式，下列结果中正确的是（　　）

A、（x﹣2）² B、（x+2）² C、x（x﹣4）+4 D、（x﹣2）（x+2）

查看试题解析
9. 已知实数a、b满足a+b＝0，且ab≠0，则 $\frac{b}{a} + \frac{a}{b}$ 的值为（　　）

A、﹣2 B、﹣1 C、1 D、2

查看试题解析
10. 如图所示，把一个长方形纸片沿EF折叠后，点D，C分别落在D′，C′的位置．若∠EFB=65°，则∠AED′等于（）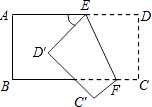

A、70° B、65° C、50° D、25°

查看试题解析

二、填空题

11. 计算： $\frac{1}{a + 1} + \frac{a}{a + 1} =$ ．

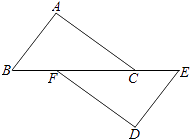
查看试题解析
12. 点 $A (3 ， - 2)$ 关于y轴对称的点的坐标是．

查看试题解析
13. 若代数式 $\frac{x}{x - 4}$ 有意义，则实数x的取值范围是．

查看试题解析
14. 如图，在△ABC和△DEF中，点B、F、C、E在同一直线上，BF=CE，AC∥DF，请添加一个条件，使△ABC≌△DEF，这个添加的条件可以是．（只需写一个，不添加辅助线）

查看试题解析
15. 已知x+y＝10，xy＝1，则代数式x²y+xy²的值为．

查看试题解析
16. 如图，在 $△ A B C$ 中， $A B = A C$ ， $∠ A = 36 °$ ， AB的中垂线DE交AC于点D，交AB于点E，在下列结论中：
①BD平分 $∠ A B C$ ；②点D是线段AC的中点：③ $A D = B D = B C$ ；④ $△ B D C$ 的周长等于 $A B + B C$ ．
正确结论的序号是．

查看试题解析

三、解答题

17. 如图，在△ABC中，AB＝AC，点D在AB上，点E在AC上，AD＝AE．求证：CD＝BE．

查看试题解析
18. 分解因式：

(1)、x²﹣4；

(2)、2a（b+c）﹣3（b+c）．

查看试题解析
19. 如图所示的方格纸中，每个小方格的边长都是1，点A（﹣4，1）B（﹣3，3）C（﹣1，2）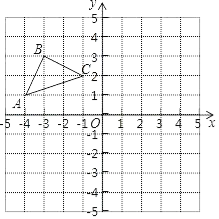
（ 1 ）作△ABC关于y轴对称的△A′B′C′；
（ 2 ）在x轴上找出点P，使PA+PC最小，并直接写出P点的坐标．

查看试题解析
20. 计算：

(1)、（﹣5y²）³；

(2)、 $\frac{4 x}{3 y}$ • $\frac{y}{2 x^{3}}$ ；

(3)、4（x+1）²﹣（2x+3）（2x﹣3）．

查看试题解析
21. 如图，在Rt△ABC中，∠C＝90°，∠CAB的平分线交BC于点D，又DE是AB的垂直平分线，垂足为E．

(1)、求∠CAD的大小；

(2)、若BC＝3，求DE的长．

查看试题解析
22.

(1)、解方程： $\frac{2}{x - 3} = \frac{3}{x}$ ；

(2)、已知 $\frac{a}{2} = \frac{b}{3}$ ≠0，求代数式 $\frac{5 a - 2 b}{a^{2} - 4 b^{2}}$ •（a﹣2b）的值．

查看试题解析
23. 如图所示，△ABC是等边三角形，D点是AC的中点，延长BC到E，使CE=CD．

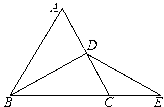(1)、用尺规作图的方法，过D点作DM⊥BE，垂足是M；（不写作法，保留作图痕迹）

(2)、求证：BM=EM．

查看试题解析
24. 星期天，小明和小军在同一小区门口同时出发，沿相同路线去离该小区1800米的青少年宫参加羽毛球训练，为响应“节能环保，绿色出行”的号召，两人都步行前往．已知小明的速度是小军的速度的1.2倍，小明比小军提前6分钟到达，求两人的速度．

查看试题解析
25. 如图①，在△ABC中，∠B＝45°，∠C＝30°，过点A作直线AC的垂线交BC于点D．

(1)、求∠BAD的度数；

(2)、若AC＝2 $\sqrt{2}$ ，求AB的长；

(3)、如图②，过点A作∠DAC的角平分线交BC于点P，点D关于直线AP的对称点为E，试探究线段CE与BD之间的数量关系，并对结论给予证明．

查看试题解析