广东省佛山市南海区2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-07-07 类型：期末考试

进入出卷网下载

一、单选题

1. 9的平方根是( )

A、3　 B、±3　　 C、 $\sqrt{3}$ 　　 D、± $\sqrt{3}$

查看试题解析
2. 下列各数 $\frac{π}{3}$ ， $3.14159265$ ， $\sqrt{8}$ ， $- 8$ ， $\sqrt[3]{9}$ ， $\sqrt{36}$ ， $\frac{22}{7}$ 中，无理数有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
3. 已知点A的坐标是（1，2），则点A关于x轴的对称点的坐标是（）

A、（1，﹣2） B、（﹣1，2） C、（﹣1，﹣2） D、（2，1）

查看试题解析
4. 下列条件中，不能判断△ABC为直角三角形的是（　　）

A、a＝5，b＝12，c＝13 B、a：b：c＝3：4：5 C、∠A+∠B＝80° D、∠A：∠B：∠C＝1：1：2

查看试题解析
5. 下列计算正确的是（　　）

A、 $\sqrt{12} - \sqrt{3} = \sqrt{3}$ B、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ C、 $3 \sqrt{5} \times \sqrt{5} = 4 \sqrt{5}$ D、 $(2 \sqrt{2})^{2} = 4 \sqrt{2}$

查看试题解析
6. 一次函数 $y = \frac{1}{2} x - 1$ 的图象与y轴交点是（　　）

A、（﹣1，0） B、（2，0） C、（0，1） D、（0，﹣1）

查看试题解析
7. 以下是二元一次方程2x+3y＝8的正整数解有（　　）

A、 ${\begin{array}{l} x = 4 \\ y = 0 \end{array}$ B、 ${\begin{array}{l} x = 2 \\ y = \frac{4}{3} \end{array}$ C、 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ D、 ${\begin{array}{l} x = 1 \\ y = 3 \end{array}$

查看试题解析
8. 甲、乙、丙、丁四个旅游团的游客人数都相等，且每个旅游团游客的平均年龄都是35岁，这四个旅游团游客年龄的方差分别为S_甲²＝6，S_乙²＝1.8，S_丙²＝5，S_丁²＝8，这四个旅游团中年龄相近的旅游团是（　　）

A、甲团 B、乙团 C、丙团 D、丁团

查看试题解析
9. 下列命题为真命题的是（　　）

A、同位角相等 B、三角形的外角等于两个内角的和 C、相等的角是对顶角 D、全等三角形的对应角相等

查看试题解析
10. 如图，直线y＝kx+b（k≠0）与x轴交于点（﹣5，0），下列说法正确的是（　　）

A、k＞0，b＜0 B、直线y＝bx+k经过第四象限 C、关于x的方程kx+b＝0的解为x＝﹣5 D、若（x₁ ， y₁），（x₂ ， y₂）是直线y＝kx+b上的两点，若x₁＜x₂ ，则y₁＞y₂

查看试题解析

二、填空题

11. 如图，以直角三角形的三边向外作正方形，其面积分别是25，169和B，则B的值是．

查看试题解析
12. 比较实数的大小：3 $\sqrt{11}$ （填“＞”、“＜”或“＝”）．

查看试题解析
13. 一次函数y＝kx+b与y＝x+2的图象交点在y轴上，则关于x，y的二元一次方程组 ${\begin{array}{l} y = k x + b \\ y = x + 2 \end{array}$ 的解是．

查看试题解析
14. 小明八年级上学期数学期中成绩是110分，期末是115分，若学期的总评成绩是根据如图的权重计算，则小明该学期的数学总评成绩为分．

查看试题解析
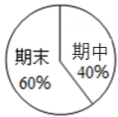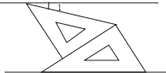
15.
如图，将一副三角板和一张对边平行的纸条按下列方式摆放，两个三角板的一直角边重合，含30°角的直角三角板的斜边与纸条一边重合，含45°角的三角板的一个顶点在纸条的另一边上，则∠1的度数是．

查看试题解析
16. 如图，一架秋千静止时，踏板离地的垂直高度DE＝0.5m，将它往前推送1.5m（水平距离BC＝1.5m）时，秋千的踏板离地的垂直高度BF＝1m，秋千的绳索始终拉直，则绳索AD的长是 m．

查看试题解析
17. 如图，在单位为1的方格纸上，△A₁A₂A₃ ， △A₃A₄A₅ ， △A₅A₆A₇ ， …，都是斜边在x轴上，斜边长分别为2，4，6，…的等腰直角三角形，若△A₁A₂A₃的顶点坐标分别为A₁（2，0），A₂（1，1），A₃（0，0）．则依图中所示规律，A₂₀₂₁的坐标为．

查看试题解析

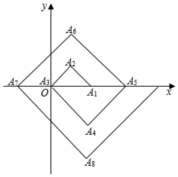
三、解答题

18. 计算： $\sqrt{6} \times \sqrt{\frac{4}{3}} - \frac{1}{\sqrt{2}} + \sqrt{(- 2)^{2}}$

查看试题解析
19. 解二元一次方程组： ${\begin{array}{l} x - 2 y = 2 \\ \frac{3}{8} x + \frac{1}{4} y = 1 \end{array}$

查看试题解析
20. 如图，已知A（1，2），B（1，﹣4），C（﹣4，﹣2）．

(1)、△ABC的面积是．

(2)、在坐标系中作出△ABC关于y轴对称的图形ΔA₁B₁C₁ ．

查看试题解析
21. 某市举行知识大赛，A校，B校各派出5名选手组成代表队参加决赛，两校派出选手的决赛成绩如图所示．

(1)、根据图示填写如表：

平均数/分
中位数/分
众数/分
A校
B校
85
100

(2)、结合两校成绩的平均数和中位数，分析哪个学校的决赛成绩较好．

查看试题解析
22. 如图，已知 $C D ∥ E F$ ， MD平分∠ADC，∠2＝∠3，

(1)、求证： $M D ∥ B C$ ．

(2)、若EF⊥AB，BD＝2，求BC的长．

查看试题解析

23. 为庆祝“中国共产党的百年华诞”，某校请广告公司为其制作“童心向党”文艺活动的展板、宣传册和横幅，其中制作宣传册的数量是展板数量的5倍，广告公司制作每件产品所需时间和利润如下表：

产品	展板	宣传册	横幅
制作一件产品所需时间（小时）	1	$\frac{1}{5}$	$\frac{1}{2}$
制作一件产品所获利润（元）	20	3	10

(1)、若制作三种产品共计需要25小时，所获利润为450元，求制作展板、宣传册和横幅的数量；

(2)、若广告公司所获利润为700元，且三种产品均有制作.求制作三种产品总量的最小值.

查看试题解析

24. 如图，在直角坐标系中，A（1，4），B（1，1），C（5，1），点D是x轴上的动点．

(1)、四边形ABDC的面积是；

(2)、当直线AD平分△ABC的面积时，求此时直线的表达式；

(3)、当△ACD的面积是10时，直接写出点D的坐标．

查看试题解析
25. 我们知道，等腰三角形的两个底角相等，它反映了边与角的转化关系．
如图，△ABC是等腰三角形，AB＝AC，我们可以用几何语言表示如下：

∵AB＝AC

∴∠B＝∠C

如图1，现在有△ABC，点D是AC的中点，E是BC上．一点，将△CDE沿DE折叠到△FDE，连接AF．

(1)、设∠DAF＝α，∠DCF＝β，则∠DFA＝， ∠DFC＝（结果用含α或β式子表示）．

(2)、求证： $D E ∥ A F$ ．

(3)、如图2，当点E与点B重合时，AB平分∠CAF，若∠AFD＝56°，求∠ABD的度数．

查看试题解析

	平均数/分	中位数/分	众数/分
A校
B校	85		100