安徽省合肥市长丰县2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-07-07 类型:期末考试
一、单选题
-
1. 下列图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,∠1=∠2,添加下列条件仍不能判定△ABD≌△ACD的是( )
2. 如图,∠1=∠2,添加下列条件仍不能判定△ABD≌△ACD的是( ) A、∠3=∠4 B、BD=CD C、∠B=∠C D、AB=AC3. 如图,在ABC中,∠C=90°,分别以A、B为圆心画弧,所画的弧交于两点,再连接该两点所在直线交BC于点D,连接AD.若BD=2,则AD的长为( )
A、∠3=∠4 B、BD=CD C、∠B=∠C D、AB=AC3. 如图,在ABC中,∠C=90°,分别以A、B为圆心画弧,所画的弧交于两点,再连接该两点所在直线交BC于点D,连接AD.若BD=2,则AD的长为( )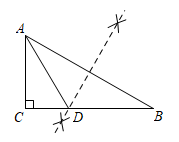 A、 B、 C、1 D、24. 下列命题中,是真命题的是( )A、三角形的外角大于该三角形任意一个内角 B、如果点P(x,y)的坐标满足xy<0,那么点P一定在第二象限 C、如果两个直角三角形,有两组边分别相等,则这两个直角三角形全等 D、如果一个等腰三角形的一个内角为60°,那么这个三角形是等边三角形5. 等腰三角形一边长5cm,另一边长2cm,则该三角形的周长是( )A、9cm B、12cm C、12cm或9cm D、7cm6. 已知点P(a-1,a+2)在x轴上,那么点Q(-a,a-1)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 将一次函数y=kx+2的图象向下平移3个单位长度后经过点(-2,1),则k的值为( )A、-1 B、2 C、1 D、-28. 小明上午8:00从家里出发,跑步去他家附近的抗日纪念馆参加抗美援朝70周年纪念活动,然后从纪念馆原路返回家中,小明离家的路程y(米)和经过的时间x(分)之间的函数关系如图所示,下列说法错误的是( )
A、 B、 C、1 D、24. 下列命题中,是真命题的是( )A、三角形的外角大于该三角形任意一个内角 B、如果点P(x,y)的坐标满足xy<0,那么点P一定在第二象限 C、如果两个直角三角形,有两组边分别相等,则这两个直角三角形全等 D、如果一个等腰三角形的一个内角为60°,那么这个三角形是等边三角形5. 等腰三角形一边长5cm,另一边长2cm,则该三角形的周长是( )A、9cm B、12cm C、12cm或9cm D、7cm6. 已知点P(a-1,a+2)在x轴上,那么点Q(-a,a-1)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 将一次函数y=kx+2的图象向下平移3个单位长度后经过点(-2,1),则k的值为( )A、-1 B、2 C、1 D、-28. 小明上午8:00从家里出发,跑步去他家附近的抗日纪念馆参加抗美援朝70周年纪念活动,然后从纪念馆原路返回家中,小明离家的路程y(米)和经过的时间x(分)之间的函数关系如图所示,下列说法错误的是( ) A、从小明家到纪念馆的路程是1800米 B、小明从家到纪念馆的平均速度为180米/分 C、小明在纪念馆停留45分钟 D、小明从纪念馆返回家中的平均速度为100米/分9. 若y=(m-1)x+m2-1是y关于x的正比例函数,如果A(1,a)和B(-1,b)在该函数的图象上,那么a和b的大小关系是( )A、 B、 C、 D、10. 如图,在△ABC中,AB=AC=12,点E在边AC上,AE的中垂线交BC于点D,若∠ADE=∠B,CD=3BD,则AE等于( )
A、从小明家到纪念馆的路程是1800米 B、小明从家到纪念馆的平均速度为180米/分 C、小明在纪念馆停留45分钟 D、小明从纪念馆返回家中的平均速度为100米/分9. 若y=(m-1)x+m2-1是y关于x的正比例函数,如果A(1,a)和B(-1,b)在该函数的图象上,那么a和b的大小关系是( )A、 B、 C、 D、10. 如图,在△ABC中,AB=AC=12,点E在边AC上,AE的中垂线交BC于点D,若∠ADE=∠B,CD=3BD,则AE等于( ) A、4 B、6 C、8 D、10
A、4 B、6 C、8 D、10二、填空题
-
11. 函数y= 中,自变量x的取值范围是.12. 在平面直角坐标系中,将点P先向左平移2个单位,再向下平移3个单位,得到的点坐标是(-3,1),则点P的坐标为 .13. 将一副三角尺按如图所示的方式摆放,则的大小为 .
 14. 已知:如图,平分 , 于E,于F,且 .
14. 已知:如图,平分 , 于E,于F,且 .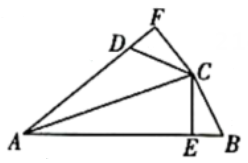 (1)、若 , , 则 .(2)、若的面积是 , 的面积是16,则的面积等于 .
(1)、若 , , 则 .(2)、若的面积是 , 的面积是16,则的面积等于 .三、解答题
-
15. 如图,在ABC和CDE中,点B、D、C在同一直线上,已知∠ACB=∠E,AC=CE,ABDE,求证:ABC≌CDE.
 16. 如图,AD、AE、AF分别是ABC的高线、角平分线和中线.
16. 如图,AD、AE、AF分别是ABC的高线、角平分线和中线. (1)、若 , CF=4,求AD的长.(2)、若∠C=70°,∠B=26°,求∠DAE的度数.17. 如图,在等腰△ABC中,BA=BC,AD平分∠BAC,DE∥AC,求证:∠ADB=3∠EDA.
(1)、若 , CF=4,求AD的长.(2)、若∠C=70°,∠B=26°,求∠DAE的度数.17. 如图,在等腰△ABC中,BA=BC,AD平分∠BAC,DE∥AC,求证:∠ADB=3∠EDA. 18. 如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2、4、6、…,顶点依次用、、、、…表示.
18. 如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2、4、6、…,顶点依次用、、、、…表示. (1)、请直接写出、、、的坐标;(2)、根据规律,求出的坐标;19. 根据国家发展改革委和生态环境部颁布的《关于进一步加强塑料污染治理的意见》,某塑料生产公司提前做好了转型升级,经过市场研究购进一批可降解吸管生产设备,并绘制出了吸管的销售收入y1与销售量x的关系和吸管的销售成本y2与销售量x的关系,如图所示.
(1)、请直接写出、、、的坐标;(2)、根据规律,求出的坐标;19. 根据国家发展改革委和生态环境部颁布的《关于进一步加强塑料污染治理的意见》,某塑料生产公司提前做好了转型升级,经过市场研究购进一批可降解吸管生产设备,并绘制出了吸管的销售收入y1与销售量x的关系和吸管的销售成本y2与销售量x的关系,如图所示. (1)、求函数和的表达式;(2)、当销售量x满足条件时,该公司盈利(即销售收入大于成本).20. 如图,在△ABC中,∠A=90°,BD平分∠ABC交AC于点D,AB=4,BC=12,AD=3,若点P在BC上运动.
(1)、求函数和的表达式;(2)、当销售量x满足条件时,该公司盈利(即销售收入大于成本).20. 如图,在△ABC中,∠A=90°,BD平分∠ABC交AC于点D,AB=4,BC=12,AD=3,若点P在BC上运动. (1)、求线段DP的最小值;(2)、当DP最小时,求CDP的面积.21. 如图,∠AOB=30°,按下列步骤作图:
(1)、求线段DP的最小值;(2)、当DP最小时,求CDP的面积.21. 如图,∠AOB=30°,按下列步骤作图:①在射线OA上取一点C,以点O为圆心,OC长为半径作圆弧DE,交射线OB于点F,连接CF;
②以点F为圆心,CF长为半径作圆弧,交弧DE于点G;
③连接FG、CG,作射线OG.根据以上作图过程及所作图形完成下列问题.
 (1)、求证:OF垂直平分CG.(2)、求证:OCG为等边三角形22. 某商场同时购进甲乙两种商品共300件,其进价和售价如下表,设购进甲种商品x件,销售完300件商品的总利润为y元.
(1)、求证:OF垂直平分CG.(2)、求证:OCG为等边三角形22. 某商场同时购进甲乙两种商品共300件,其进价和售价如下表,设购进甲种商品x件,销售完300件商品的总利润为y元.商品名称
甲
乙
进价(元/件)
50
70
售价(元/件)
90
120
(1)、求y与x的函数关系式.(2)、该商品计划最多投入17000元用于购买这两种商品,若售完这些商品,则至少购进多少件甲商品商场可获得最大利润,获得的最大利润是多少元?23. 如图,在等腰△ABC与等腰△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=α,连接BD和CE相交于点P,交AC于点M,交AD于点N. (1)、求证:BD=CE.(2)、求证:AP平分∠BPE.(3)、若α=60°,试探寻线段PE、AP、PD之间的数量关系,并说明理由.
(1)、求证:BD=CE.(2)、求证:AP平分∠BPE.(3)、若α=60°,试探寻线段PE、AP、PD之间的数量关系,并说明理由.