浙江省台州市椒江区2021-2022学年七年级下学期期末数学试卷
试卷更新日期:2022-07-07 类型:期末考试
一、选择题(本题有10小题,每小题3分,共30分.)
-
1. 在平面直角坐标系中,点 在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 下列各数为无理数的是( )A、 B、 C、 D、3. 下列调查中,不适合用全面调查的是( )A、了解冬奥会开幕式的在线收视率 B、疫情期间对进入超市人员进行扫码登记 C、“神舟十四号”载人飞船发射前各零部件的检查 D、了解新冠肺炎确诊病人同机乘客的健康状况4. 若 ,则下列式子正确的是( )A、 B、 C、 D、5. 如图,点E在 的延长线上,下列条件不能判断 的是( )
 A、 B、 C、 D、6. 不等式 的解集在数轴上表示正确的是( )A、
A、 B、 C、 D、6. 不等式 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、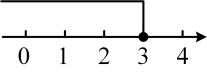 D、
D、 7. 我国古代数学著作《九章算术》“盈不足”一章中记载:“今有大器五、小器一容三解:大器一、小器五容二斛,问大小器各容几何?”意思是:今有大容器5个,小容器1个,总容量为3斛;大容器1个,小容器5个,总容量为2斛.问1个大容器、1个小容器的容量各是多少斛?设1个大容器的容量为x斛,1个小容器的容量为y斛,则下列方程组正确的是( )A、 B、 C、 D、8. 如图,从起点A到终点B有多条路径,其中第一条路径为线段 ,其长度为a , 第二条路径为折线 ,其长度为b , 第三条路径为折线 ,其长度为c , 第四条路径为半圆弧 ,其长度为d , 则这四条路径的长度关系为( )
7. 我国古代数学著作《九章算术》“盈不足”一章中记载:“今有大器五、小器一容三解:大器一、小器五容二斛,问大小器各容几何?”意思是:今有大容器5个,小容器1个,总容量为3斛;大容器1个,小容器5个,总容量为2斛.问1个大容器、1个小容器的容量各是多少斛?设1个大容器的容量为x斛,1个小容器的容量为y斛,则下列方程组正确的是( )A、 B、 C、 D、8. 如图,从起点A到终点B有多条路径,其中第一条路径为线段 ,其长度为a , 第二条路径为折线 ,其长度为b , 第三条路径为折线 ,其长度为c , 第四条路径为半圆弧 ,其长度为d , 则这四条路径的长度关系为( ) A、 B、 C、 D、9. 关于x , y的二元一次方程 ,当k取一个确定的值时就得到一个方程,所有这些方程有一个公共解,则这个公共解是( )A、 B、 C、 D、10. 如图,平面直角坐标系内有一条折线从原点O出发后,在第一象限内曲折前行,已知 , ; , ;依照这个规律,其中 , , ,…,则 的坐标是( )
A、 B、 C、 D、9. 关于x , y的二元一次方程 ,当k取一个确定的值时就得到一个方程,所有这些方程有一个公共解,则这个公共解是( )A、 B、 C、 D、10. 如图,平面直角坐标系内有一条折线从原点O出发后,在第一象限内曲折前行,已知 , ; , ;依照这个规律,其中 , , ,…,则 的坐标是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本题有6小题,每小题4分,共24分)
-
11. 点 关于y轴的对称点的坐标是.12. 请写出关于x , y的二元一次方程 的一个解:.13. 中学生骑电动车上学给交通安全带来一定的隐患,为了了解某中学1500名学生的家长对“中学生骑电动车上学”的态度,交通部门从中随机抽取了500名家长进行问卷调查.在这个调查中,样本容量是.14. 如图,在马路旁有一个村庄,现要在马路l上设立一个核酸检测点为方便该村村民参加核酸检测,核酸检测点最好设在处,理由是.
 15. 如图,小明把图1中长与宽分别为3和5的两个长方形纸片裁剪成四个一模一样的直角三角形,并将这四个直角三角形纸片拼成如图2所示的一个大正方形,则图2这个大正方形的边长为.
15. 如图,小明把图1中长与宽分别为3和5的两个长方形纸片裁剪成四个一模一样的直角三角形,并将这四个直角三角形纸片拼成如图2所示的一个大正方形,则图2这个大正方形的边长为. 16. 若不等式(组)①的解集中的任意解都满足不等式(组)②,则称不等式(组)①被不等式(组)②覆盖,特别的,若一个不等式(组)无解,则它被其他任意不等式(组)覆盖.例如:不等式 被不等式 覆盖;不等式组 无解,它被其他任意不等式(组)覆盖.若关于x的不等式组 ,被 覆盖,则a的取值范围是.
16. 若不等式(组)①的解集中的任意解都满足不等式(组)②,则称不等式(组)①被不等式(组)②覆盖,特别的,若一个不等式(组)无解,则它被其他任意不等式(组)覆盖.例如:不等式 被不等式 覆盖;不等式组 无解,它被其他任意不等式(组)覆盖.若关于x的不等式组 ,被 覆盖,则a的取值范围是.三、解答题(本题有8小题,第17~19题每题6分,第20~21题每题8分,第22~23题每题10分,第24题12分,共66分)
-
17. 计算: .18. 解方程组:19. 三角形 在平面直角坐标系 中的位置如图所示.
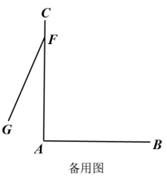
 (1)、写出三角形的顶点A , B两点的坐标;(2)、三角形 中任意一点 经平移后对应点为 将三角形 作同样的平移得到三角形 ,请画出三角形 ;(3)、求三角形 的面积.20. 如图,已知 于点A , 交 于点E , 且 于点F.
(1)、写出三角形的顶点A , B两点的坐标;(2)、三角形 中任意一点 经平移后对应点为 将三角形 作同样的平移得到三角形 ,请画出三角形 ;(3)、求三角形 的面积.20. 如图,已知 于点A , 交 于点E , 且 于点F.
求证: .
证明:∵ 于点A , 于点F , (已知)
∴ . (垂直的定义)
∴ , ( )
∴▲ ( )
∵ ,(已知)
∴ ▲ . (两直线平行,同位角相等)
∵ ,
∴ . (等量代换)
21. 2022年3月以来,受全国新冠疫情的影响,椒江区教育系统积极响应区委区政府的号召,组织了1896名教师志愿者助力区域核酸检测的防疫工作.教师们放下粉笔,穿上“新装”,化身社区里的“红马甲”、“大白”身边的“小蓝”,在“疫”线绽放别样光芒.为了了解这些教师志愿者在3月份至5月份期间参加防疫工作的时间情况,随机抽取了其中的50名教师志愿者进行问卷调查,并对数据进行了整理和描述,部分信息如下图表:防疫时间的频数分布表
时间x/小时
频数
频率
0≤x<5
8
0.16
5≤x<10
12
0.24
10≤x<15
16
b
15≤x<20
11
0.22
20≤x<25
a
0.06

请根据所给信息,解答下列问题:
(1)、a= , b=;(2)、请补全频数分布直方图;(3)、请估计这1896名教师志愿者中,3月份至5月份期间参加防疫工作的时间不低于10小时的约有多少人(结果精确到个位)?22. 我们知道,负数没有算术平方根,但对于三个互不相等的负整数,若两两乘积的算术方根都是整数,则称这三个数为“完美组合数”.例如:-9,-4,-1这三个数, , , ,其结果6,3,2都是整数,所以-1,-4,-9这三个数称为“完美组合数”.
(1)、-18,-8,-2这三个数是“完美组合数”吗?请说明理由.(2)、若三个数-3,m , -12是“完美组合数”,其中有两个数乘积的算术平方根为12,求m的值.23. 北京冬奥会吉祥物“冰墩墩”和北京冬残奥会吉祥物“雪容融”一上市,就深受大家的喜爱.某特许商店准备在2022年2月上架“冰墩墩”和“雪容融”这两款毛绒玩具.第一周用7400元购进“冰墩墩”50个和“雪容融”30个;第二周又用12800元购进“冰墩墩”80个和“雪容融”60个.(1)、请分别求出每个“冰墩墩”和“雪容融”的进价.(2)、进入2022年3月后,随着冬残奥会的召开,“冰墩墩”和“雪容融”持续热销.于是该商店准备再购进这两款毛绒玩具共500个,其中“雪容融”的数量不超过“冰墩墩”数量的2倍,且所用资金不超过43400元,试问有哪几种进货方案?24. 已知射线 射线 于点A , 点D , F分别在射线 , 上,过点D , F作射线 , ,使 ,如下图所示. (1)、试判断直线 与直线 的位置关系,并说明理由.(2)、如下图,已知 的角平分线与 的角平分线相交于点P.
(1)、试判断直线 与直线 的位置关系,并说明理由.(2)、如下图,已知 的角平分线与 的角平分线相交于点P.
①当 时,则 ▲ ;
②当 ( )时, 的大小是否保持不变?若不变,请说明理由;若改变,请求出 的度数.
(3)、当 沿射线 平移且 时,请直接写出 的角平分线与 的角平分线所在直线相交形成的 的度数.