浙江省宁波市宁海县2021-2022学年八年级下学期期末数学试卷

试卷更新日期：2022-07-07 类型：期末考试

进入出卷网下载

一、选择题（每小题3分，共30分，）

1. 下列方程中，属于一元二次方程的是（）

A、x﹣2y＝1 B、x²﹣2x+1＝0 C、x²﹣2y+4＝0 D、x²+3＝ $\frac{2}{x}$

查看试题解析
2. 若要使式子 $\sqrt{x - 2}$ 有意义，则x的值可以是（）

A、0 B、1 C、﹣1 D、4

查看试题解析
3. 下列几何图形中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 下列计算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $\sqrt{(- 2)^{2}} = - 2$ C、 $\sqrt{2} \times \sqrt{8} = 4$ D、 $2 \sqrt{2} - \sqrt{2} = 2$

查看试题解析
5. 甲、乙、丙、丁四位选手各10次射击成绩的平均数和方差如表所示：

选手

甲

乙

丙

丁

平均数（环）

7

8

8

7

方差（环2）

0.9

1.1

0.9

1

则这四人中成绩好且发挥最稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
6. 用反证法证明命题“在直角三角形中，至少有一个锐角不大于45°”时，应先假设（　　）

A、有一个锐角小于45° B、每一个锐角都小于45° C、有一个锐角大于45° D、每一个锐角都大于45°

查看试题解析
7. 下列条件中，不能判定四边形ABCD是平行四边形的是（）

A、∠A＝∠C，∠B＝∠D B、AD∥BC，AB＝CD C、AB∥CD，AD∥BC D、AB∥CD，AB＝CD

查看试题解析
8. 已知点A（x₁ ， y₂），B（x₁ ， y₂）都在反比例函数y＝ $\frac{2}{x}$ 的图象上，且x₁＜x₂＜0，则y₁ ， y₂的大小关系是（）

A、0＜y₁＜y₂ B、y₁＜y₂＜0 C、0＜y₂＜y₁ D、y₂＜y₁＜0

查看试题解析
9. 如图，在△ABC中，延长BC至点D，使得CD＝ $\frac{1}{2}$ BC，过AC的中点E作EF∥CD（点F位于点E右侧），且EF＝BC，连接DF，若AB＝4，则DF的长为（）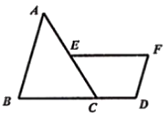

A、3 B、2 C、2 $\sqrt{2}$ D、 $\sqrt{3}$

查看试题解析
10. 如图，正方形AMNP和正方形EFGH是两个全等的正方形，将它们按如图的方式放置在正方形ABCD内，若求阴影图形的面积，则只需知道（）

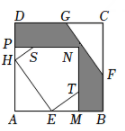A、△AHE的面积 B、五边形HETNS的面积 C、△EMT的面积 D、正方形AMNP的面积

查看试题解析

二、填空题（每题4分，共24分）

11. 当x=1时，二次根式 $\sqrt{4 - 2 x}$ 的值为．

查看试题解析
12. 已知一个多边形的内角和是720度，则这个多边形是边形．

查看试题解析
13. 某大学自主招生考试只考数学和物理，计算综合得分时，数学占60%，物理占40%．已知小慧数学得分为95分，物理得分为80分，则小慧的综合得分是分．

查看试题解析
14. 关于x的一元二次方程x²+2x+k＝0有两个不相等的实数根，则k的取值范围是．

查看试题解析
15. 某同学用如图1中的一副七巧板拼成如图2的“帆船图”，已知正方形ABCD的边长为4，则图2中h的值为．

查看试题解析
16. 如图，点D是 ▱ ABCD内一点，CD∥x轴，BD∥y轴，BD＝ $\sqrt{2}$ ，∠ADB＝135°，S_△ABD＝2，若反比例函数y＝ $\frac{k}{x}$ （x＜0）的图象经过A、D两点，则k的值是．

查看试题解析

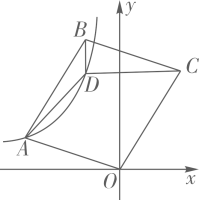
三、解答题（本大题有8小题，共66分）

17. 计算：

(1)、 $\sqrt{40} \div \sqrt{2} - \sqrt{5}$ ；

(2)、（ $\sqrt{6}$ ﹣2）（ $\sqrt{6}$ +2）﹣ $\sqrt{3}$ （2 $\sqrt{3}$ ﹣2）．

查看试题解析
18. 解方程：

(1)、x²﹣3x＝0；

(2)、x²﹣4x+3＝0．

查看试题解析
19. 某社区为了增强居民节约用水的意识，随机调查了部分家庭一年的月均用水量（单位：t）．根据调查结果，绘制出如下的统计图①和图②．

请根据相关信息，解答下列问题：

（Ⅰ）本次接受调查的家庭个数为，图①中m的值为；

（Ⅱ）求统计的这组月均用水量数据的平均数、众数和中位数．

查看试题解析
20. 如图，在正方形ABCD中，点E，F为对角线BD上两点，CE＝CF．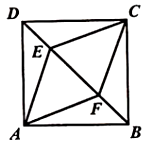

(1)、求证：四边形AFCE是菱形．

(2)、若EF＝6，DE＝BF＝3，求四边形AECF的周长．

查看试题解析
21. 如图，在平面直角坐标系中，O是坐标原点，反比例函数y₁＝ $\frac{k}{x}$ 的图象与正比例函数y₂＝2x的图象交于A，B两点，点C在x轴正半轴上，AC＝AO，△ACO的面积为8．

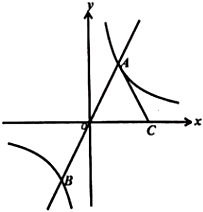(1)、求k的值和B点的坐标；

(2)、根据图象直接写出y₁＞y₂时x的取值范围．

查看试题解析
22. 2022年冬奥会在北京顺利召开，冬奥会吉祥物冰墩墩公仔爆红．据统计冰墩墩公仔在某电商平台1月份的销售量是5万件，3月份的销售量是7.2万件．

(1)、若该平台1月份到3月份的月平均增长率都相同，求月平均增长率是多少？

(2)、市场调查发现，某一间店铺冰墩墩公仔的进价为每件60元，若售价为每件100元，每天能销售20件，售价每降价1元，每天可多售出2件，为了推广宣传，商家决定降价促销，同时尽量减少库存，若使销售该公仔每天获利1200元，则售价应降低多少元？

查看试题解析
23. 在项目化学习“折纸中的数学”中，有同学以“矩形纸片的折叠”开展探究活动．现有矩形纸片ABCD（AD＞AB），点E在线段BC上，折痕为AE，点B的对应点为点F，分别按以下操作回答问题．

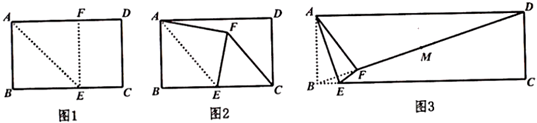(1)、如图1，若点F落在线段AD上，则四边形ABEF是哪类特殊四边形？答：．

(2)、如图2，若点F落在矩形纸片ABCD内，满足CF∥AE，此时线段BE与AD有怎样的数量关系，并说明理由．

(3)、如图3，点F落在对角线BD上，点M为矩形的对称中心，且AB＝MF，求∠ABD的度数．

查看试题解析
24. 若一个四边形有一组邻边相等，且这组邻边夹角所对的对角线平分一个内角，则称这样的四边形为“近似菱形”．例如：如图1，在四边形ABCD中，AB＝AD，BD平分∠ABC，则四边形ABCD是近似菱形．

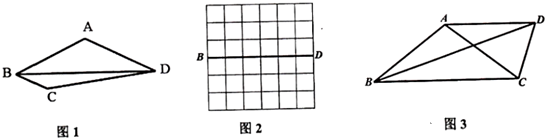(1)、请在图2中作出一个以BD为对角线的“近似菱形”ABCD，顶点A、顶点C要在网格格点上．

(2)、如图3，在四边形ABCD中，AB＝AC，AD∥BC，∠CAD＝2∠DBC．求证：四边形ABCD是“近似菱形”．

(3)、在（2）的条件下，若BD＝3，CD＝1，求AB的长．

查看试题解析

选手	甲	乙	丙	丁
平均数（环）	7	8	8	7
方差（环2）	0.9	1.1	0.9	1