四川省达州市渠县2021-2022学年七年级下学期期末数学试卷
试卷更新日期:2022-07-07 类型:期末考试
一、单选题
-
1. 甲骨文是我国古代的一种文字,是汉字的早期形式,反映了我国悠久的历史文化,体现了我国古代劳动人民的智慧,下列甲骨文中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若a为正整数,则=( )A、a2a B、2aa C、aa D、3. 奥密克戎是新型冠状病毒的一种变异株,它给全球人民带来了巨大的灾难,冠状病毒的直径约80﹣120nm,1nm为十亿分之一米,即m,将95nm用科学记数法表示正确的是( )米.A、9.5× B、9.5× C、95× D、0.95×4. 木工师傅将一把三角尺和一个重锤如图放置,就能检查一根横梁是否水平,能解释这一现象的数学知识是( )
2. 若a为正整数,则=( )A、a2a B、2aa C、aa D、3. 奥密克戎是新型冠状病毒的一种变异株,它给全球人民带来了巨大的灾难,冠状病毒的直径约80﹣120nm,1nm为十亿分之一米,即m,将95nm用科学记数法表示正确的是( )米.A、9.5× B、9.5× C、95× D、0.95×4. 木工师傅将一把三角尺和一个重锤如图放置,就能检查一根横梁是否水平,能解释这一现象的数学知识是( ) A、角平分线定理 B、等腰三角形的三线合一 C、线段垂直平分线定理 D、两直线垂直的性质5. 如图,AB//CD,EF=DF,若∠A=50°,则∠E 等于( )
A、角平分线定理 B、等腰三角形的三线合一 C、线段垂直平分线定理 D、两直线垂直的性质5. 如图,AB//CD,EF=DF,若∠A=50°,则∠E 等于( ) A、50° B、55° C、60° D、65°6. 如图,在中, , . 用无刻度的直尺和圆规在AB边上找一点D,使 , 则符合要求的作图是( )A、
A、50° B、55° C、60° D、65°6. 如图,在中, , . 用无刻度的直尺和圆规在AB边上找一点D,使 , 则符合要求的作图是( )A、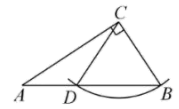 B、
B、 C、
C、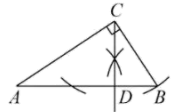 D、
D、 7. 下列乘法公式的运用,正确的是( )A、(-x+y)(y+x)=x2-y2 B、(a-3)2=a2-9 C、(2x-3)(2x+3)=4x2-9 D、(4x+1)2=16x2-8x+18. 下列说法正确是( )A、概率很小的事情不可能发生 B、投掷一枚质地均匀的硬币1000次,正面朝上的次数一定是500次 C、从1、2、3、4、5中任取一个数是偶数的可能性比较大 D、13名同学中,至少有两人的出生月份相同是必然事件9. 若一个等腰三角形的周长为32,则该等腰三角形的腰长x的取值范围是( )A、0<x<32 B、0<x<16 C、8<x<16 D、8<x<3210. 已知A、B两地相距600米,甲、乙两人同时从A地出发前往B地,所走路程y(米)与行驶时间x(分)之间的函数关系如图所示,则下列说法中:①甲每分钟走100米;②2分钟后,乙每分钟走50米;③甲比乙提前3分钟到达B地;④当x=2或6时,甲乙两人相距100米.其中,正确的是( )
7. 下列乘法公式的运用,正确的是( )A、(-x+y)(y+x)=x2-y2 B、(a-3)2=a2-9 C、(2x-3)(2x+3)=4x2-9 D、(4x+1)2=16x2-8x+18. 下列说法正确是( )A、概率很小的事情不可能发生 B、投掷一枚质地均匀的硬币1000次,正面朝上的次数一定是500次 C、从1、2、3、4、5中任取一个数是偶数的可能性比较大 D、13名同学中,至少有两人的出生月份相同是必然事件9. 若一个等腰三角形的周长为32,则该等腰三角形的腰长x的取值范围是( )A、0<x<32 B、0<x<16 C、8<x<16 D、8<x<3210. 已知A、B两地相距600米,甲、乙两人同时从A地出发前往B地,所走路程y(米)与行驶时间x(分)之间的函数关系如图所示,则下列说法中:①甲每分钟走100米;②2分钟后,乙每分钟走50米;③甲比乙提前3分钟到达B地;④当x=2或6时,甲乙两人相距100米.其中,正确的是( ) A、①②③ B、②③④ C、①②④ D、①②
A、①②③ B、②③④ C、①②④ D、①②二、填空题
-
11. 一辆汽车以70km/h的速度在高速路上匀速行驶,则该汽车行驶的路程S(km)与时间t(h)之间的关系式是 , 其中自变量是 , 因变量是.12. 大数据分析技术为打赢疫情防控阻击战发挥了重要作用,如图是张老师的健康码示意图,用黑白打印机打印在边长为2cm的正方形区域内,图中黑色部分的总面积为2.4cm2 , 现在向正方形区域内随机掷点,点落入黑色部分的概率为.
 13. 如图,爱思考的小红观看舞蹈时,发现某一时刻的情形抽象成数学问题:如图,已知ABCD,∠BAE=93°,∠DCE=116°,则∠E的度数是.
13. 如图,爱思考的小红观看舞蹈时,发现某一时刻的情形抽象成数学问题:如图,已知ABCD,∠BAE=93°,∠DCE=116°,则∠E的度数是. 14. 若 , 则.15. 小芳和小林为了研究图中“跑到画板外面去的两直线a,b所成的角(锐角)”问题,设计出如下两个方案:
14. 若 , 则.15. 小芳和小林为了研究图中“跑到画板外面去的两直线a,b所成的角(锐角)”问题,设计出如下两个方案:

现在小林只测得∠β=115°,小芳作了AB=BC,并只测得∠1=80°,请你根据以上信息求出直线a,b所成角的度数.
16. 如图,等腰直角△ABC中,∠BAC=90°,ADBC于D,∠ABC的平分线分别交AC、AD于E、F两点,M为EF的中点,延长AM交BC于点N,连接DM,NE.下列结论:①AE=AF;②AM⊥EF;③△AEF是等边三角形;④DF=DN;⑤ADEN.其中正确的结论有.
三、解答题
-
17. 计算(1)、(2)、(2x3y)3(-2xy)+(-2x3y)3÷(2x2)18. 先化简,再求值 , 其中 , .19. 如图,在正方形网格中,△ABC的顶点都在格点上,∠ACB=90°,AC=BC,点C在直线MN上,请完成下列问题:
 (1)、画出△ABC关于直线MN的对称图形;(2)、连接 , 交AC于D,若∠BCN=59°,画出图形,并求∠ADB的度数.20. 如图,在△ABC中,AC=BC,∠B=42°,点D是边AB上一点,点B关于直线CD的对称点为 , 当AC时,求∠BCD的度数.
(1)、画出△ABC关于直线MN的对称图形;(2)、连接 , 交AC于D,若∠BCN=59°,画出图形,并求∠ADB的度数.20. 如图,在△ABC中,AC=BC,∠B=42°,点D是边AB上一点,点B关于直线CD的对称点为 , 当AC时,求∠BCD的度数.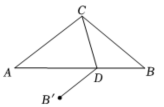 21. 课堂上老师给了一个问题:
21. 课堂上老师给了一个问题:已知:如图,ABCD,EFAB于点O,FG交CD于点P,当∠1=30°时,求∠EFG的度数.

同学们讨论后,发现解决此问题有多种思路:思路一:过点F作MNCD(如图(1));
思路二:过点P作PNEF,交AB于点N.......;

按要求解答下列问题:
(1)、根据思路一图(1),可求得∠EFG的度数为:;(2)、根据思路二在图(2)中作出符合要求的图形,试写出求∠EFG的度数的解答过程.22. 【数学试验】数学学习小组在学习“用频率估计概率”的数学活动课上,做投掷骰子(质地均匀的正方体)试验,他们共做了100次试验,试验的结果如下:
向上点数
1
2
3
4
5
6
出现次数
12
19
15
18
20
x
(1)、求表格中x的值;(2)、计算“3点朝上”的频率.(3)、【数学发现】数学学习小组针对数学试验的结果提出结论:“根据试验及‘用频率估计概率’的知识,出现1点朝上的概率是12%.”你认为数学学习小组的结论正确吗?并说明理由.(4)、【结论应用】在一个不透明的盒子里,装有40个黑球和若干个白球,它们除颜色外都相同,搅匀后从中任意摸出一个球,记下颜色再把它放回盒子中,不断重复试验,统计结果发现,随着试验次数越来越多,摸到黑球的频率逐渐稳定在0.2左右.据此估计盒子中大约有白球多少个?23. 完全平方公式:(a±b)2=a2±2ab+b2 , 适当的变形,可以解决很多的数学问题.例如:若a+b=3,ab=1,求a2+b2的值.解:因为a+b=3,
所以(a+b)2=9,即:a2+2ab+b2=9,又因为ab=1
所以a2+b2=7
根据上面的解题思路与方法,解决下列问题:
(1)、若x+y=8,x2+y2=40,求xy的值;(2)、填空:若(4-x)(x-5)=-8,则(4-x)2+(x-5)2=;(3)、如图,点C是线段AB上的一点,以AC、BC为边向两边作正方形,设AB=6,两正方形的面积和S1+S2=18,求图中阴影部分面积.
 24. ∠MON=90°,点A,B分别在OM、ON上运动(不与点O重合).
24. ∠MON=90°,点A,B分别在OM、ON上运动(不与点O重合). (1)、如图①,AE、BE分别是∠BAO和∠ABO的平分线,随着点A、点B的运动,∠AEB=;(2)、如图②,若BC是∠ABN的平分线,BC的反向延长线与∠OAB的平分线交于点D.
(1)、如图①,AE、BE分别是∠BAO和∠ABO的平分线,随着点A、点B的运动,∠AEB=;(2)、如图②,若BC是∠ABN的平分线,BC的反向延长线与∠OAB的平分线交于点D.①若∠BAO=60°,则∠D= ▲ ;
②随着点A,B的运动,∠D的大小会变吗?如果不会,求∠D的度数:如果会,请说明理由.
25. 问题发现:如图1,∠AOB=90°,OC平分∠AOB,把三角尺的直角顶点落在OC的任意一点P上,并使三角尺的两条直角边分别与OA、OB相交于点E、F.探究发现PE=PF(可以这样想:作PMOA于点M,PNOB于点N,易得PM=PN,∠PME=∠PNF=90°,∠MPE=∠NPF=90°-∠EPN,所以△PNM△PNF,所以PE=PF)变式拓展:如图2,已知∠AOB=120°,OC平分∠AOB,P是OC上一点,∠EPF=60°,PE边与OA边相交于点E,PF边与射线OB的反向延长线相交于点F.
 (1)、PE与PF还相等吗?请说明理由;(2)、试判断OE、OF、OP三条线段之间的数量关系,并说明理由.
(1)、PE与PF还相等吗?请说明理由;(2)、试判断OE、OF、OP三条线段之间的数量关系,并说明理由.