江苏省苏州市吴江区2021-2022学年七年级下学期期末数学试卷
试卷更新日期:2022-07-07 类型:期末考试
一、单选题
-
1. 计算结果正确的是( )A、 B、 C、 D、2. 如图,在数轴上,点、分别表示数、 , 且.若 , 则点表示的数为( )
 A、 B、 C、2 D、43. 仔细观察下列图形,其中∠1与∠2是内错角的是( )A、
A、 B、 C、2 D、43. 仔细观察下列图形,其中∠1与∠2是内错角的是( )A、 B、
B、 C、
C、 D、
D、 4. 在△ABC中,如果∠A﹣∠B=90°,那么△ABC是( )A、直角三角形 B、钝角三角形 C、锐角三角形 D、斜三角形5. 如图,在Rt△ABC中,∠A=35°,则∠B=( )
4. 在△ABC中,如果∠A﹣∠B=90°,那么△ABC是( )A、直角三角形 B、钝角三角形 C、锐角三角形 D、斜三角形5. 如图,在Rt△ABC中,∠A=35°,则∠B=( ) A、45° B、55° C、65° D、145°6. 若的结果中不含项,则的值为( )A、0 B、2 C、 D、-27. 已知方程组 , 则的值是( )A、 B、2 C、 D、48. 如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,则∠3的度数为( )
A、45° B、55° C、65° D、145°6. 若的结果中不含项,则的值为( )A、0 B、2 C、 D、-27. 已知方程组 , 则的值是( )A、 B、2 C、 D、48. 如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,则∠3的度数为( ) A、 B、 C、 D、9. 从前,古希腊一位庄园主把一块长为a米,宽为b米()的长方形土地租给租户张老汉,第二年,他对张老汉说:“我把这块地的长增加10米,宽减少10米.维续租给你,租金不变,你也没有吃亏,你看如何?”如果这样,你觉得张老汉的租地面积会( )A、变小了 B、变大了 C、没有变化 D、无法确定10. 如图,在 中, 是边 上的点, 是边 上的点,且 , ,若 的面积为1,则 的面积为( )
A、 B、 C、 D、9. 从前,古希腊一位庄园主把一块长为a米,宽为b米()的长方形土地租给租户张老汉,第二年,他对张老汉说:“我把这块地的长增加10米,宽减少10米.维续租给你,租金不变,你也没有吃亏,你看如何?”如果这样,你觉得张老汉的租地面积会( )A、变小了 B、变大了 C、没有变化 D、无法确定10. 如图,在 中, 是边 上的点, 是边 上的点,且 , ,若 的面积为1,则 的面积为( )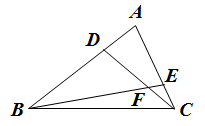 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算: = .12. 已知:am=10,an=2,则am+n= .13. 若 , 则.14. 北斗卫星导航系统可在全球范围内全天候、全天时为各类用户提供高精度、高可靠的定位、导航、授时服务,其授时精度为10纳秒,1纳秒为1秒的十亿分之一,用科学记数法表示其授时精度为秒.15. 如果一个正多边形的一个内角是135°,则这个正多边形是.16. 如图,在中,平分 , DEAC,若 , , 那么.
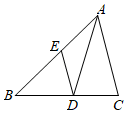 17. 如图,若ABCDEF,则∠x,∠y,∠z三者之间的数量关系是.
17. 如图,若ABCDEF,则∠x,∠y,∠z三者之间的数量关系是. 18. 如图,直线上有两点、 , 分别引两条射线、 , 与在直线异侧.若 , 射线、分别绕点,点以度秒和度秒的速度同时顺时针转动,设时间为秒,在射线转动一周的时间内,当时间的值为时,与平行.
18. 如图,直线上有两点、 , 分别引两条射线、 , 与在直线异侧.若 , 射线、分别绕点,点以度秒和度秒的速度同时顺时针转动,设时间为秒,在射线转动一周的时间内,当时间的值为时,与平行.
三、解答题
-
19. 计算:20. 因式分解:21.(1)、解方程组:;(2)、解不等式组:.22. 如图,已知 , , 、、三点共线,连接交于点.
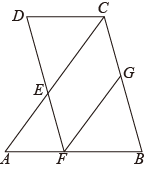 (1)、求证:;(2)、若 , , 求的度数.23. 在图中,利用网格点和三角板画图或计算:
(1)、求证:;(2)、若 , , 求的度数.23. 在图中,利用网格点和三角板画图或计算: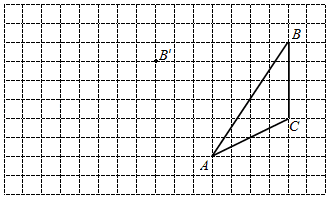 (1)、在给定方格纸中画出平移后的△A'B'C;(2)、图中AC与A'C′的关系怎样?(3)、记网格的边长为1,则△A'B′C′的面积为多少?24. 小明到文具店买文具.请你根据对话信息(小明:阿姨您好,我要买12支中性笔和20本笔记本,是不是一共112元?店员:不对呀,一共是144元.小明:啊……哦,我明白了,您是对的!我刚才把中性笔和笔记本的单价弄反了),求中性笔和笔记本的单价分别是多少元?
(1)、在给定方格纸中画出平移后的△A'B'C;(2)、图中AC与A'C′的关系怎样?(3)、记网格的边长为1,则△A'B′C′的面积为多少?24. 小明到文具店买文具.请你根据对话信息(小明:阿姨您好,我要买12支中性笔和20本笔记本,是不是一共112元?店员:不对呀,一共是144元.小明:啊……哦,我明白了,您是对的!我刚才把中性笔和笔记本的单价弄反了),求中性笔和笔记本的单价分别是多少元? 25. 如图,现有以下三个条件:①②③.请你以其中两个作为题设,另一个作为结论构造命题.
25. 如图,现有以下三个条件:①②③.请你以其中两个作为题设,另一个作为结论构造命题. (1)、你构造的是哪几个命题?(2)、你构造的命题是真命题还是假命题?若是真命题,请给予证明;若是假命题,请举出反例(证明其中的一个命题即可).26. 在3×3的方格中,每行、每列及对角线上的3个代数式的和都相等,我们把这样的方格图叫做“等和格”. 如图1的“等和格”中,每行、每列及对角线上的3个代数式的和都等于15.
(1)、你构造的是哪几个命题?(2)、你构造的命题是真命题还是假命题?若是真命题,请给予证明;若是假命题,请举出反例(证明其中的一个命题即可).26. 在3×3的方格中,每行、每列及对角线上的3个代数式的和都相等,我们把这样的方格图叫做“等和格”. 如图1的“等和格”中,每行、每列及对角线上的3个代数式的和都等于15. (1)、在图2的“等和格”方格图中,可得a=.(用含b的代数式表示);(2)、在图3的“等和格”方格图中,可得a= , b=;(3)、在图4的“等和格”方格图中,可得b=.27. 如图1,将一副三角板中的两个直角顶点叠放在一起,其中 , , .
(1)、在图2的“等和格”方格图中,可得a=.(用含b的代数式表示);(2)、在图3的“等和格”方格图中,可得a= , b=;(3)、在图4的“等和格”方格图中,可得b=.27. 如图1,将一副三角板中的两个直角顶点叠放在一起,其中 , , .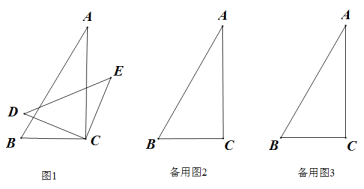 (1)、观察猜想,∠BCD与∠ACE的数量关系是;∠BCE与∠ACD的数量关系是;(2)、类比探究,若按住三角板不动,顺时针绕直角顶点转动三角形 , 试探究当∠ACD等于多少度时CE//AB,画出图形并简要说明理由;(3)、拓展应用,若∠BCE=3∠ACD,求∠ACD的度数;并直接写出此时DE与AC的位置关系.28. 已知关于x,y的方程组(1)、请直接写出方程x+2y-6=0的所有正整数解;(2)、若方程组的解满足x+y=0,求m的值;(3)、无论实数m取何值时,方程x-2y+mx+5=0总有一个固定的解,求出这个解.(4)、若方程组的解中x恰为整数,m也为整数,求m的值.
(1)、观察猜想,∠BCD与∠ACE的数量关系是;∠BCE与∠ACD的数量关系是;(2)、类比探究,若按住三角板不动,顺时针绕直角顶点转动三角形 , 试探究当∠ACD等于多少度时CE//AB,画出图形并简要说明理由;(3)、拓展应用,若∠BCE=3∠ACD,求∠ACD的度数;并直接写出此时DE与AC的位置关系.28. 已知关于x,y的方程组(1)、请直接写出方程x+2y-6=0的所有正整数解;(2)、若方程组的解满足x+y=0,求m的值;(3)、无论实数m取何值时,方程x-2y+mx+5=0总有一个固定的解,求出这个解.(4)、若方程组的解中x恰为整数,m也为整数,求m的值.