河南省商丘市梁园区2021-2022学年七年级下学期期末数学试卷

试卷更新日期：2022-07-07 类型：期末考试

进入出卷网下载

一、单选题

1. 平方根等于它本身的数是（）

A、0 B、 $- 1$ C、1 D、 $± 1$

查看试题解析
2. 在平面直角坐标系中，点 $P (- 3 ， 2)$ 在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 已知a＞b ，则下列不等式成立的是（）

A、a+3＞b+4 B、2a＜2b C、a﹣1＞b﹣1 D、﹣4a＞﹣4b

查看试题解析
4. 下列调查中，适宜采用全面调查方式的是（）

A、调查某品牌水笔的使用寿命 B、了解我省中学生学生的视力情况 C、调查乘坐飞机的乘客是否携带违禁物品 D、了解我省中学生课外阅读情况

查看试题解析
5. 如图，给出下列条件：①∠1＝∠2；②∠3＝∠4；③AB∥CE，且∠ADC=∠B，④AB∥CE，且∠BCD＝∠BAD；其中能推出BC∥AD的条件为（）

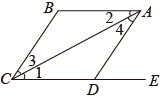A、①② B、②④ C、②③ D、②③④

查看试题解析
6. 若 $a^{2}$ ＝2， $b$ ＝ $\sqrt{2}$ ，由实数 $a$ 、 $b$ 组成的有序数对（ $a$ ， $b$ ）在平面直角坐标系第二象限，则 $a + b$ 的值为（）

A、2 $\sqrt{2}$ B、﹣2 $\sqrt{2}$ C、0 D、2 $\sqrt{2}$ 或﹣2 $\sqrt{2}$

查看试题解析
7. 已知点 $P (a ， a + 1)$ 在平面直角坐标系的第二象限，则 $a$ 的取值范围在数轴上可表示为（）.

A、 B、 C、 D、

查看试题解析
8. 今年，小丽爷爷的年龄是小丽的5倍.小丽发现，12年之后，爷爷的年龄是小丽的3倍，设今年小丽、爷爷的年龄分别是 $x$ 岁、 $y$ 岁，可列方程组（）

A、 ${\begin{array}{l} x = 5 y \\ x + 12 = 3 y \end{array}$ B、 ${\begin{array}{l} x = 5 y \\ 3 x = y \end{array}$ C、 ${\begin{array}{l} 5 x = y \\ 3 (x + 12) = y \end{array}$ D、 ${\begin{array}{l} 5 x = y \\ 3 (x + 12) = y + 12 \end{array}$

查看试题解析
9. 如图，将一条上下两边互相平行的纸带折叠，设∠1为 $x$ 度，则 $∠ α =$ （）

A、 $x$ B、 $90 ° - \frac{1}{2} x$ C、 $180 ° - x$ D、 $2 x$

查看试题解析
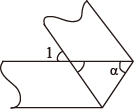10. 从−2，−1，0，2，5这五个数中，随机抽取一个数记为m，若数m使关于x的不等式组 ${\begin{array}{l} x > m + 2 \\ - 2 x - 1 ⩾ 4 m + 1 \end{array}$ 无解，且使关于x的一元一次方程（m−2）x=3有整数解，那么这五个数中所有满足条件的m的个数有（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 已知a，b是两个连续整数，且a＜ $\sqrt{3} + 1$ ＜b，则 $b^{a}$ ＝.

查看试题解析
12. 如图，直线 $A B$ 、 $C D$ 相交于点 $O$ ， $∠ C O E$ 是直角， $O F$ 平分 $∠ B O E$ ， $∠ A O C = 18 °$ ，则 $∠ E O F$ 的度数为.

查看试题解析
13. 已知 ${\begin{array}{l} x = a \\ y = b \end{array}$ ，是方程组 ${\begin{array}{l} x + 2 y = 8 \\ 2 x + y = 7 \end{array}$ 的解，则 $a - b$ 的值为.

查看试题解析
14. 对于x，符号[x]表示不大于x的最大整数.如：[3.14]＝3，[﹣7.59]＝﹣8，则满足关系式 $[\frac{3 x + 7}{7}] = 4$ 的x的整数值有个.

查看试题解析
15. 如图，在平面直角坐标系中，将正方形①依次平移后得到正方形②，③，④…；相应地，顶点A依次平移得到A₁ ， A₂ ， A₃ ， …，其中A点坐标为（1，0），A₁坐标为（0，1），则A₂₀的坐标为．

查看试题解析

三、解答题

16.

(1)、计算： $\sqrt{7} - \sqrt[3]{- 27} - | \sqrt{7} - 4 | - \sqrt{{(- 5)}^{2}}$ ；

(2)、解方程组： ${\begin{array}{l} y = 2 x - 3 \\ 4 x - 3 y = 1 \end{array}$ ；

(3)、解方程组 ${\begin{array}{l} 3 (x - 1) = y + 5 \\ 5 (y - 1) = 3 (x + 5) \end{array}$

查看试题解析
17. 解下列不等式或不等式组：

(1)、 $1 - \frac{7 x - 1}{8} > \frac{3 x - 2}{4}$

(2)、 ${\begin{array}{l} 2 x - 1 \geq x \\ x + 5 < 4 x - 1 \end{array}$

查看试题解析
18. 已知点 $A (- 2 ， 2)$ ， $B (3 a + 1 ， 2 + a)$ ，且 $A B / / x$ 轴，解答下列各题：

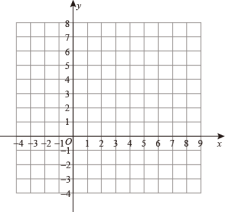(1)、点 $B$ 的坐标为；

(2)、在平面直角坐标系中画出三角形 $A B O$ ，然后将这个三角形向右平移3个单位长度，再向上平移2个单位长度，得三角形 $D E F$ ，点 $D$ ， $E$ ， $F$ ，分别是平移后点 $A$ ， $B$ ， $O$ 的对应点，画出平移后的三角形 $D E F$ ；

(3)、三角形 $D E F$ 的面积为.

查看试题解析
19. 某学校为了解该校七年级学生疫情防控知识的情况，对七年级共400名学生进行了测试，从中随机抽取40名学生的成绩（百分制）进行整理、描述，得到部分信息：
a.这40名学生成绩的频数分布直方图如图（数据分成5组： $50 \leq x < 60$ ， $60 \leq x < 70$ ， $70 \leq x < 80$ ， $80 \leq x < 90$ ， $90 \leq x \leq 100$ ；）
b.成绩在 $80 \leq x < 90$ 这一组的是：89 89 88 88 88 87 87 86 85 84 84 83 82 80 80 80 80
c.成绩不低于85为优秀.
根据以上信息，回答问题：

(1)、补全频数分布直方图；

(2)、下面说法正确的是.
①本次抽样调查的样本容量是40；
②样本中，成绩为100分的学生不超过6人.

(3)、估计该校七年级400名学生成绩优秀的人数.

查看试题解析
20. 已知：如图，三角形 $A B C$ 中， $A C ⊥ B C$ ， $F$ 是边 $A C$ 上的点，连接 $B F$ ，作 $E F ∥ B C$ 且交 $A B$ 于点 $E$ .过点 $E$ 作 $D E ⊥ E F$ ，交 $B F$ 于点 $D$ .
求证： $∠ 1 + ∠ 2 = 180 °$ .
下面是证明过程，请在横线上填上适当的推理结论或推理依据.
证明：∵ $A C ⊥ B C$ （已知），
∴ $∠ A C B = 90 °$ （   ）.
∵ $E F ∥ B C$ （已知），
∴ $∠ A F E =$   ▲   $= 90 °$ （   ）
∵ $D E ⊥ E F$ （已知），
∴ $∠ D E F = 90 °$ （   ）.
∴ $∠ A F E = ∠ D E F$ （等量代换）.
∴  ▲   $∥$   ▲  （   ）.
∴ $∠ 2 = ∠ E D F$ （   ）.
又∵ $∠ E D F + ∠ 1 = 180 °$ （   ）.
∴ $∠ 1 + ∠ 2 = 180 °$ （等量代换）.

查看试题解析
21. 在“一带一路”建设中，中国水稻专家将“杂交水稻之父”袁隆平院士的水稻培育技术带到了非洲.在我国专家驻地附近的A村有稻田100亩，B村有稻田200亩，在技术指导前A、B两村的水稻总产量仅80吨.经过我国专家的指导后，现在A村的水稻平均亩产量比原来提高了50%，B村的水稻平均亩产量比原来提高了40%，A、B两村的水稻总产量共114吨.

(1)、请分别求出原来A、B两村水稻的平均亩产量：

(2)、经过我国专家技术指导之后，A村的水稻出米率为80%，且A、B两村的水稻加工后大米的总重量不低于82.8吨，那么B村的水稻出米率至少为多少？（注：出米率=加工后大米的重量 $\div$ 加工前水稻的重量）

查看试题解析
22. 已知关于x、y的方程组 ${\begin{array}{l} x - y = 11 - m \\ x + y = 7 - 3 m \end{array}$ .

(1)、当m＝2时，请解关于x、y的方程组 ${\begin{array}{l} x - y = 11 - m \\ x + y = 7 - 3 m \end{array}$ ；

(2)、若关于x、y的方程组 ${\begin{array}{l} x - y = 11 - m \\ x + y = 7 - 3 m \end{array}$ 中，x为非负数、y为负数，
①试求m的取值范围；
②当m取何整数时，不等式3mx+2x＞3m+2的解为x＜1.

查看试题解析
23. 如图，在平面直角坐标系xOy中，已知 $A (4 ， 0)$ ，将线段 $O A$ 平移至 $C B$ ，点D在x轴正半轴上， $C (a ， b)$ ，且 $\sqrt{a - 2} + | b - 3 | = 0$ .连接OC，AB，CD，BD.

(1)、写出点C的坐标为；点B的坐标为；

(2)、当 $△ O D C$ 的面积是 $△ A B D$ 的面积的3倍时，求点D的坐标；

(3)、设 $∠ O C D = α$ ， $∠ D B A = β$ ， $∠ B D C = θ$ ，判断 $α$ 、 $β$ 、 $θ$ 之间的数量关系，并说明理由.

查看试题解析