初中数学暑假作业（人教版：七年级升八年级）：01相交线与平行线
试卷更新日期：2022-07-07 类型：同步测试
一、单选题
-
1. 下列各图中，和是对顶角的是（ ）A、
B、
C、
D、
2. 点为直线外一点，点 ， ， 为直线上三点， ， ， ， 则点到直线的距离为（ ）A、 B、 C、小于 D、不大于3. 如图，三角形ABC中，∠ACB＝∠CDB＝90°，则点C到直线AB的距离是（ ）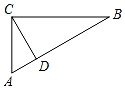
A、线段CA的长 B、线段AD的长 C、线段CB的长 D、线段CD的长4. 如图，下列各角与∠A是同位角的是（ ）
A、∠1 B、∠2 C、∠3 D、∠45. 下列说法错误的个数是（ ）①经过一点有且只有一条直线与已知直线平行；
②垂直于同一条直线的两条直线互相平行；
③直线外一点到这条直线的垂线段，叫做这个点到直线的距离；
④同一平面内不相交的两条直线叫做平行线．
A、1个 B、2个 C、3个 D、4个6. 如图，下面哪个条件能判断DE∥BC的是（ ）
A、∠1＝∠2 B、∠4＝∠C C、∠1+∠3＝180° D、∠3+∠C＝180°7. 如图，给出下列四个条件：①AC=BD；②∠DAC=∠BCA；③∠ABD=∠CDB；④∠ADB=∠CBD，其中能使AD∥BC的条件是（ ）
A、①② B、②④ C、③④ D、①③④8. 一把含45°角的三角尺和一把直尺按如图所示的方式摆放，若∠1=20°，则∠2的度数为（ ）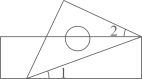
A、15° B、20° C、25° D、40°9. 下列语句描述中，属于命题的是（ ）A、对顶角相等 B、作线段AB=CD C、AB与CD是否相等 D、点到直线的距离10. 如图所示的图案是一些汽车的车标，可以看作由“基本图案”经过平移得到的是（ ）A、
B、
C、
D、
二、填空题
-
11. 如图，为了方便人们从A点到道路l上，学校过A点作直线l垂线，垂足为B点，这样做的数学原理是 .
12. 如图，给出下列四个条件：①AC=BD；②∠DAB=∠BCA；③∠ABD= ∠CDB；④∠ADB=∠CBD其中能使AD∥BC的条件是 ．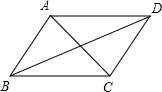
13. 如图，直线 ， 若∠1=123°，则∠2=.
14. 已知三条不同的直线a、b、c在同一平面内，下列四条命题：①如果a∥b，a⊥c，那么b⊥c；②如果b∥a，c∥a，那么b∥c；③如果b⊥a，c⊥a，那么b⊥c；④如果b⊥a，c⊥a，那么b∥c．其中假命题的是 ． （填写序号）
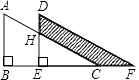
15. 如图，将△ABC沿水平方向向右平移到△DEF的位置，已知点A、D之间的距离为1，CE=3，则BF的长为 ．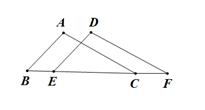
三、解答题
-
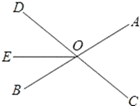
16. 如图，直线AB、CD相交于点O，∠AOC=70°，OE把∠BOD分成两部分，且∠BOE：∠EOD=2：3，求∠AOE的度数．
17. 如图，直线AB，CD相交于点O，OE⊥CD于点O，∠EOB=115°，求∠AOC的度数.请补全下面的解题过程（括号中填写推理的依据）.
解：∵OE⊥CD于点O（已知），
∴_▲_（ ）.
∵∠EOB=115°（已知），
∴∠DOB=_▲__=115°-90°=25°.
∵直线AB，CD相交于点O（已知），
∴∠AOC=_▲_=25°（ ）.
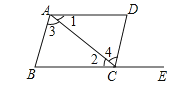
18.如图，
（1）指出直线AB，CD被AC所截形成的内错角；
（2）指出直线AB，CD被BE所截形成的同位角；
（3）找出图中∠1的所有同旁内角
19. 如图所示，已知AB⊥BC，∠1+∠2=90°，∠2=∠3．BE与FD平行吗？为什么？将下面的解答过程补充完整．
解：BE∥FD．理由如下：
∵AB⊥BC，
∴∠ABC=▲
即∠3+∠4=▲ °
又∵∠1+∠2=90°，
且∠2=∠3，
∴ ▲ =▲ （ ），
∴BE∥FD（ ）．
20. 如图所示，直线AB，CD相交于点O，OD平分．∠EOB，OF平分∠AOE，GH⊥CD，垂足为点H，GH与FO平行吗？说明理由．
