（人教版）2022年暑假八年级数学复习巩固专题7 矩形
试卷更新日期：2022-07-06 类型：复习试卷
一、单选题
-
1. 如图，D、E为边AB、AC上的中点，F为线段DE上的一点，若 ， ， ， 则线段EF的长为（ ）
A、4 B、3 C、2 D、12. 如图，两个全等的矩形AEFG，矩形ABCD如图所示放置．CD所在直线与AE，GF分别交于点H，M．若AB＝3，BC＝ ，CH＝MH．则线段MH的长度是（ ）
A、 B、 C、 D、23. 如图，Rt△ABC中，∠ABC＝90°，点O是斜边AC的中点，AC＝10，则OB＝（ ）
A、5 B、6 C、8 D、104. 有下列四个条件：①对角线互相平分的四边形；②对角线互相垂直的四边形；③对角线相等的平行四边形；④有一个角是直角的平行四边形，其中能作为矩形的判定条件的是（ ）A、①② B、③④ C、①③ D、②④5. 如图，矩形ABCD中，对角线AC的垂直平分线分别交AD、BC于点E、F，垂足为O，若 ， ， 则EF的长为（ ）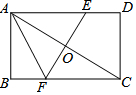
A、 B、 C、 D、6. 如图，矩形的对角线、相交于点 ， ， ， 则的长为（ ）
A、6 B、 C、 D、7. 在Rt△ABC中，∠C＝90°，CD是AB边上的中线，下列结论正确的是（ ）A、CD⊥AB B、CD＝BC C、BD＝CD D、∠ACD＝∠BCD8. 如图，在Rt△ABC中，∠BAC=90°，AB=3，AC=4，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF的中点，则AM的最小值是（ ）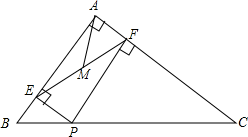
A、 B、 C、 D、9. 如图，在Rt△ABC中，∠ACB＝90°，∠A＝65°，CD⊥AB，垂足为D，E是BC的中点，连接ED，则∠DEC的度数是（ ）
A、50° B、40° C、30° D、25°10. 矩形不一定具有的性质是（ ）A、对边相等 B、对角相等 C、邻边相等 D、对角线相等二、填空题
-
11. 如图， 中， ，以AB为边在三角形外的 的对角线交于点F，AE=2，AB=5，则CF的最大值是 ．
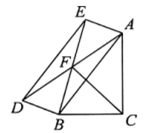12. 在平面直角坐标系中，点 ， 连接 ， 若点D是的中点，连接 ， 则的长为.13. 如图，在正方形ABCD中，点E在对角线AC上，EF⊥AB于点F，EG⊥BC于点G，连接FG，若AB＝8，则FG的最小值为 ．
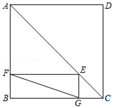14. 两直角边分别为6和8的直角三角形，斜边上的中线的长是 ．15. 如图，在矩形ABMN中，AN＝ ， 点C是MN的中点，分别连接AC，BC，且BC＝2 ， 点D为AC的中点，点E为边AB上一个动点，连接DE，点A关于直线DE的对称点为点F，分别连接DF，EF，当EF⊥AC时，AE的长为 ．
三、解答题
-
16. 如图，两根直立的竹竿相距6m，高分别为4m和7m，求两竹竿顶端间的距离AD．
17. 如图，在 ABCD中，以AC为斜边作Rt△ACE，且∠BED是直角.求证： ABCD是矩形.
18. 如图，在四边形 中， ， ，点 ， 分别是边 ， 的中点，且 .求证：四边形 是平行四边形.
19. 如图，将平行四边形ABCD的边DC延长到点E ， 使CE＝DC ， 连结AE ， 交BC于点F ， ∠AFC＝2∠D ， 连结AC、BE ． 求证：四边形ABEC是矩形．
20. 已知：如图，在△ABC中，AB＝AC，D为BC中点，四边形ABDE是平行四边形．求证：四边形ADCE是矩形．
