（人教版）2022年暑假七年级数学复习巩固专题13 坐标方法的简单应用
试卷更新日期：2022-07-06 类型：复习试卷
一、单选题
-
1. 根据下列表述，能够确定位置的是（ ）A、某市位于北纬30°，东经120° B、一只风筝飞到距A处20米处 C、甲地在乙地的正东方向上 D、影院座位位于一楼二排2. 云南是一个神奇美丽的地方，这里有美丽的边疆、美丽的城市、美丽的村庄、美丽的风情，云南的省会城市昆明更有着四季如春的美誉．下 列表示昆明市地理位置最合理的是（ ）A、在中国西南方 B、在云贵高原的中部 C、距离北京2600公里 D、东经102°、北纬24°3. 小敏出学校向南走1500m，再向东走2000m到家，如果以学校位置为原点，以正东、正北方向为x轴、y轴正方向建立平面直角坐标系，规定一个单位长度代表1m，则小敏家用有序数对表示为（ ）A、（2000 ，1500） B、（2000，-1500） C、（-2000，1500） D、（-2000，-1500）4. 如图是某市部分平面示意图，为准确表示地理位置，可以建立平面直角坐标系用坐标表示地理位置，若汽车站的坐标是 ， 图书馆的坐标是 ， 则火车站的坐标为（ ）
A、 B、 C、 D、5. 如图是老北京城一些地点的分布示意图，在图中，分别以正东，正北方向为 轴， 轴的正方向建立平面直角坐标系．如果表示东直门的点的坐标为（3.5，4），表示宣武门的点的坐标为（－2，－1），那么坐标原点所在的位置是（ ）
A、天安门 B、正阳门 C、西直门 D、阜成门6. 已知点P（−2，5），Q（n，5）且PQ=4，则n的值为（ ）A、2 B、2或4 C、2或−6 D、−67. 在平面直角坐标系中，点A（x，y），B（4，3），AB＝4，且AB//y轴，则A点的坐标为（ ）A、（4，7） B、（4，﹣1） C、（0，3），或（8，3） D、（4，7），或（4，﹣1）8. 已知线段AB ， 点A的坐标为(3，3)，点B的坐标为(2，6)，线段AB平移变换后得到线段 ，已知点A的对应点 的坐标为(6，6)，那么点 的坐标为（ ）A、(5，6) B、(2，9) C、(5，9) D、(﹣1，3)9. 如图，点A ， B的坐标分别为(2，0)，(0，1)，若将线段AB平移至A1B1 ， 则a+b的值为（ ）
A、2 B、3 C、5 D、810. 若点 先向右平移 个单位，再向上平移 个单位，得到点 ，若点 位于第三象限，则 的取值范围是（ ）A、 B、 C、 D、二、填空题
-
11. 在电影票上，如果将“8排4号”记作 ， 那么确定的位置是.12. 传统的棋盘式里坊格局，是大同古城显著的城市风格和特色．如图是古城内部分建筑物的平面示意图，图中小方格都是边长为1个单位长度的正方形．若魁星楼的坐标为 ， 纯阳宫的坐标为 ， 则关帝庙的坐标为 ．
13. 在平面直角坐标系中，点到x轴的距离是.14. 已知：平面直角坐标系中，点M的坐标是 ， 线段平行于y轴，且 ， 则N的坐标是 ．15. 如图，点A、B的坐标分别为（0，2）、（3，0）．若将线段AB平移至A1B1 ， 则a2+b2的值为 ．
三、解答题
-
16. 这是一所学校的平面示意图，若以校门为原点建立平面直角坐标系，请画出该坐标系，并用坐标表示校门、图书馆、教学楼、旗杆和实验楼的位置.
17. 王林同学利用暑假参观了幸福村果树种植基地 如图 ，他出发沿 的路线进行了参观，请你按他参观的顺序写出他路上经过的地方，并用线段依次连接他经过的地点．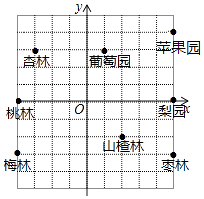
18. 如下图所示，A的位置为（2，6），小明从A出发，经（2，5）→（3，5）→（4，5）→（4，4）→（5，4）→（6，4），小刚也从A出发，经（3，6）→（4，6）→（4，7）→（5，7）→（6，7），则此时两人相距几个格?
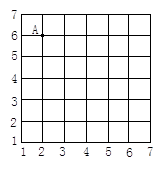19. 如图是游乐场“欢乐谷”的平面图，已知碰碰车的坐标是（﹣1，﹣1），请建立平面直角坐标系，依次写出“欢乐谷”中其它各娱乐设施 过山车、魔鬼城、跳伞塔、太空飞人、碰碰船、海盗船的坐标．
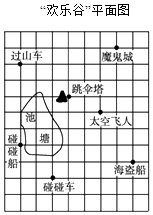20.在平面直角坐标系中，点O是坐标原点，点A的坐标是（-a，a），点B的坐标是（c，b），满足 .
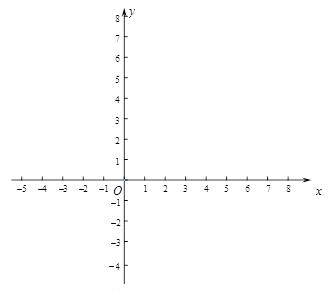(1)、a为不等式2x+6<0的最大整数解，求a的值并判断点A在第几象限；(2)、在（1）的条件下，求△AOB的面积；(3)、在（2）的条件下，若两个动点M（k-1，k），N（-2h+10，h），请你探索是否存在以两个动点M、N为端点的线段MN//AB，且MN=AB，若存在，求M、N两点的坐标；若不存在，请说明理由.