2022年全国高考物理真题汇编:牛顿运动定律
试卷更新日期:2022-07-06 类型:二轮复习
一、单选题
-
1. 如图所示,一小物块从长1m的水平桌面一端以初速度v0沿中线滑向另一端,经过1s从另一端滑落。物块与桌面间动摩擦因数为μ,g取10m/s2。下列v0、μ值可能正确的是( )
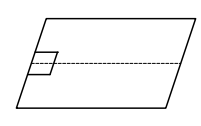 A、v0= 2.5m/s B、v0= 1.5m/s C、μ = 0.28 D、μ = 0.252. 如图所示,鱼儿摆尾击水跃出水面,吞食荷花花瓣的过程中,下列说法正确的是( )
A、v0= 2.5m/s B、v0= 1.5m/s C、μ = 0.28 D、μ = 0.252. 如图所示,鱼儿摆尾击水跃出水面,吞食荷花花瓣的过程中,下列说法正确的是( ) A、鱼儿吞食花瓣时鱼儿受力平衡 B、鱼儿摆尾出水时浮力大于重力 C、鱼儿摆尾击水时受到水的作用力 D、研究鱼儿摆尾击水跃出水面的动作可把鱼儿视为质点3. 如图是滑雪道的示意图。可视为质点的运动员从斜坡上的M点由静止自由滑下,经过水平NP段后飞入空中,在Q点落地。不计运动员经过N点的机械能损失,不计摩擦力和空气阻力。下列能表示该过程运动员速度大小v或加速度大小a随时间t变化的图像是( )
A、鱼儿吞食花瓣时鱼儿受力平衡 B、鱼儿摆尾出水时浮力大于重力 C、鱼儿摆尾击水时受到水的作用力 D、研究鱼儿摆尾击水跃出水面的动作可把鱼儿视为质点3. 如图是滑雪道的示意图。可视为质点的运动员从斜坡上的M点由静止自由滑下,经过水平NP段后飞入空中,在Q点落地。不计运动员经过N点的机械能损失,不计摩擦力和空气阻力。下列能表示该过程运动员速度大小v或加速度大小a随时间t变化的图像是( )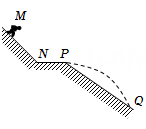 A、
A、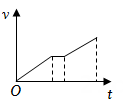 B、
B、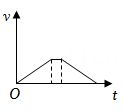 C、
C、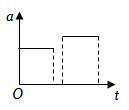 D、
D、 4. 如图,一不可伸长轻绳两端各连接一质量为m的小球,初始时整个系统静置于光滑水平桌面上,两球间的距离等于绳长L。一大小为F的水平恒力作用在轻绳的中点,方向与两球连线垂直。当两球运动至二者相距 时,它们加速度的大小均为( )
4. 如图,一不可伸长轻绳两端各连接一质量为m的小球,初始时整个系统静置于光滑水平桌面上,两球间的距离等于绳长L。一大小为F的水平恒力作用在轻绳的中点,方向与两球连线垂直。当两球运动至二者相距 时,它们加速度的大小均为( ) A、 B、 C、 D、
A、 B、 C、 D、二、多选题
-
5. 如图所示,两平行导轨在同一水平面内。一导体棒垂直放在导轨上,棒与导轨间的动摩擦因数恒定。整个装置置于匀强磁场中,磁感应强度大小恒定,方向与金属棒垂直、与水平向右方向的夹角θ可调。导体棒沿导轨向右运动,现给导体棒通以图示方向的恒定电流,适当调整磁场方向,可以使导体棒沿导轨做匀加速运动或匀减速运动。已知导体棒加速时,加速度的最大值为 g;减速时,加速度的最大值为 g,其中g为重力加速度大小。下列说法正确的是( )
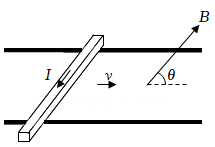 A、棒与导轨间的动摩擦因数为 B、棒与导轨间的动摩擦因数为 C、加速阶段加速度大小最大时,磁场方向斜向下,θ=60° D、减速阶段加速度大小最大时,磁场方向斜向上,θ=150°
A、棒与导轨间的动摩擦因数为 B、棒与导轨间的动摩擦因数为 C、加速阶段加速度大小最大时,磁场方向斜向下,θ=60° D、减速阶段加速度大小最大时,磁场方向斜向上,θ=150°三、综合题
-
6. 物流公司通过滑轨把货物直接装运到卡车中,如图所示,倾斜滑轨与水平面成24°角,长度l1=4m,水平滑轨长度可调,两滑轨间平滑连接。若货物从倾斜滑轨顶端由静止开始下滑,其与滑轨间的动摩擦因数均为 ,货物可视为质点(取cos24°=0.9,sin24°=0.4)。
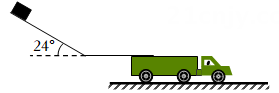 (1)、求货物在倾斜滑轨上滑行时加速度a1的大小;(2)、求货物在倾斜滑轨末端时速度v的大小;(3)、若货物滑离水平滑轨末端时的速度不超过2m/s,求水平滑轨的最短长度l2。7. 某同学受自动雨伞开伞过程的启发,设计了如图12所示的物理模型。竖直放置在水平桌面上的滑杆上套有一个滑块,初始时它们处于静止状态。当滑块从A处以初速度 为 向上滑动时,受到滑杆的摩擦力f为 ,滑块滑到B处与滑杆发生完全非弹性碰撞,带动滑杆离开桌面一起竖直向上运动。已知滑块的质量 ,滑杆的质量 ,A、B间的距离 ,重力加速度g取 ,不计空气阻力。求:
(1)、求货物在倾斜滑轨上滑行时加速度a1的大小;(2)、求货物在倾斜滑轨末端时速度v的大小;(3)、若货物滑离水平滑轨末端时的速度不超过2m/s,求水平滑轨的最短长度l2。7. 某同学受自动雨伞开伞过程的启发,设计了如图12所示的物理模型。竖直放置在水平桌面上的滑杆上套有一个滑块,初始时它们处于静止状态。当滑块从A处以初速度 为 向上滑动时,受到滑杆的摩擦力f为 ,滑块滑到B处与滑杆发生完全非弹性碰撞,带动滑杆离开桌面一起竖直向上运动。已知滑块的质量 ,滑杆的质量 ,A、B间的距离 ,重力加速度g取 ,不计空气阻力。求: (1)、滑块在静止时和向上滑动的过程中,桌面对滑杆支持力的大小 和 ;(2)、滑块碰撞前瞬间的速度大小v;(3)、滑杆向上运动的最大高度h。8. 机场地勤工作人员利用传送带从飞机上卸行李。如图所示,以恒定速率v1=0.6m/s运行的传送带与水平面间的夹角 ,转轴间距L=3.95m。工作人员沿传送方向以速度v2=1.6m/s从传送带顶端推下一件小包裹(可视为质点)。小包裹与传送带间的动摩擦因数μ=0.8。取重力加速度g=10m/s2 , sin37°=0.6,cos37°=0.8.求:
(1)、滑块在静止时和向上滑动的过程中,桌面对滑杆支持力的大小 和 ;(2)、滑块碰撞前瞬间的速度大小v;(3)、滑杆向上运动的最大高度h。8. 机场地勤工作人员利用传送带从飞机上卸行李。如图所示,以恒定速率v1=0.6m/s运行的传送带与水平面间的夹角 ,转轴间距L=3.95m。工作人员沿传送方向以速度v2=1.6m/s从传送带顶端推下一件小包裹(可视为质点)。小包裹与传送带间的动摩擦因数μ=0.8。取重力加速度g=10m/s2 , sin37°=0.6,cos37°=0.8.求: (1)、小包裹相对传送带滑动时加速度的大小a;(2)、小包裹通过传送带所需的时间t。9. 带电粒子流的磁聚焦和磁控束是薄膜材料制备的关键技术之一、带电粒子流(每个粒子的质量为 、电荷量为 )以初速度 垂直进入磁场,不计重力及带电粒子之间的相互作用。对处在 平面内的粒子,求解以下问题。
(1)、小包裹相对传送带滑动时加速度的大小a;(2)、小包裹通过传送带所需的时间t。9. 带电粒子流的磁聚焦和磁控束是薄膜材料制备的关键技术之一、带电粒子流(每个粒子的质量为 、电荷量为 )以初速度 垂直进入磁场,不计重力及带电粒子之间的相互作用。对处在 平面内的粒子,求解以下问题。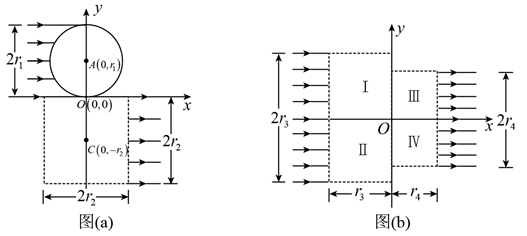 (1)、如图(a),宽度为 的带电粒子流沿 轴正方向射入圆心为 、半径为 的圆形匀强磁场中,若带电粒子流经过磁场后都汇聚到坐标原点 ,求该磁场磁感应强度 的大小;(2)、如图(a),虚线框为边长等于 的正方形,其几何中心位于 。在虚线框内设计一个区域面积最小的匀强磁场,使汇聚到 点的带电粒子流经过该区域后宽度变为 ,并沿 轴正方向射出。求该磁场磁感应强度 的大小和方向,以及该磁场区域的面积(无需写出面积最小的证明过程);(3)、如图(b),虛线框Ⅰ和Ⅱ均为边长等于 的正方形,虚线框Ⅲ和Ⅳ均为边长等于 的正方形。在Ⅰ、Ⅱ、Ⅲ和Ⅳ中分别设计一个区域面积最小的匀强磁场,使宽度为 的带电粒子流沿 轴正方向射入Ⅰ和Ⅱ后汇聚到坐标原点 ,再经过Ⅲ和Ⅳ后宽度变为 ,并沿 轴正方向射出,从而实现带电粒子流的同轴控束。求Ⅰ和Ⅲ中磁场磁感应强度的大小,以及Ⅱ和Ⅳ中匀强磁场区域的面积(无需写出面积最小的证明过程)。
(1)、如图(a),宽度为 的带电粒子流沿 轴正方向射入圆心为 、半径为 的圆形匀强磁场中,若带电粒子流经过磁场后都汇聚到坐标原点 ,求该磁场磁感应强度 的大小;(2)、如图(a),虚线框为边长等于 的正方形,其几何中心位于 。在虚线框内设计一个区域面积最小的匀强磁场,使汇聚到 点的带电粒子流经过该区域后宽度变为 ,并沿 轴正方向射出。求该磁场磁感应强度 的大小和方向,以及该磁场区域的面积(无需写出面积最小的证明过程);(3)、如图(b),虛线框Ⅰ和Ⅱ均为边长等于 的正方形,虚线框Ⅲ和Ⅳ均为边长等于 的正方形。在Ⅰ、Ⅱ、Ⅲ和Ⅳ中分别设计一个区域面积最小的匀强磁场,使宽度为 的带电粒子流沿 轴正方向射入Ⅰ和Ⅱ后汇聚到坐标原点 ,再经过Ⅲ和Ⅳ后宽度变为 ,并沿 轴正方向射出,从而实现带电粒子流的同轴控束。求Ⅰ和Ⅲ中磁场磁感应强度的大小,以及Ⅱ和Ⅳ中匀强磁场区域的面积(无需写出面积最小的证明过程)。
-