云南省玉溪市2022年初中学业水平考试模拟检测数学试题

试卷更新日期：2022-07-06 类型：中考模拟

进入出卷网下载

一、单选题

1. $- 3$ 的倒数是（）

A、 $3$ B、 $\frac{1}{3}$ C、 $- \frac{1}{3}$ D、 $- 3$

查看试题解析
2. 某小组7名学生的中考体育分数分别为37，40，39，37，40，38，40，该组数据的众数、中位数分别为（）

A、40，37 B、40，39 C、39，40 D、40，38

查看试题解析
3. 2022年北京冬奥会于2月4日开幕 $.$ 作为2022年北京冬奥会雪上项目的主要举办地，张家口市崇礼区建成7家大型滑雪场，拥有169条雪道，共162000米．数字162000用科学记数法表示为（）

A、 $162 \times 1 0^{3}$ B、 $16.2 \times 1 0^{4}$ C、 $1.62 \times 1 0^{5}$ D、 $1.62 \times 1 0^{6}$

查看试题解析
4. 下列计算正确的是（）

A、 $\sqrt{6} - \sqrt{3} = \sqrt{3}$ B、 $(- 2 x)^{3} \cdot x^{2} = - 8 x^{6}$ C、 $x^{6} \div x^{2} = x^{3}$ D、 $(- a + b) (- a - b) = a^{2} - b^{2}$

查看试题解析
5. 关于x的方程（k﹣3）x²﹣4x+2＝0有实数根，则k的取值范围是（）

A、k≤5 B、k＜5且k≠3 C、k≤5且k≠3 D、k≥5且k≠3

查看试题解析
6. 平行四边形、矩形、菱形、正方形共有的性质是（）.

A、对角线互相平分 B、对角线相等 C、对角线互相垂直 D、对角线互相垂直平分

查看试题解析
7. 不等式组 ${\begin{array}{l} x ＜ 3 \\ 1 - x \leq 0 \end{array}$ 的解集，在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
8. 点D，E分别是三角形ABC的边AB，AC的中点，如图，
求证： $D E / / B C$ 且 $D E = \frac{1}{2} B C$
证明：延长DE到F，使EF=DE，连接FC，DC，AF，
又AE=EC，则四边形ADCF是平行四边形，
接着以下是排序错误的证明过程；
① $∴ D F \underset{=}{/ /} B C$ ；
② $C F \underset{=}{/ /} A D ， C F \underset{=}{/ /} B D$ ；
③四边形DBCF是平行四边形；
④ $∴ D E / / B C ，$ 且 $∴ D E = \frac{1}{2} B C$
则正确的证明排序应是：（）

A、② $\to$ ③ $\to$ ① $\to$ ④ B、② $\to$ ① $\to$ ③ $\to$ ④ C、① $\to$ ③ $\to$ ④ $\to$ ② D、① $\to$ ③ $\to$ ② $\to$ ④

查看试题解析
9. 如图，小明利用一个锐角是 $30 °$ 的三角板测量操场旗杆的高度，已知他与旗杆之间的水平距离 $B C$ 为 $15m$ ， $A B$ 为 $1 .5m$ （即小明的眼睛与地面的距离），那么旗杆的高度是（）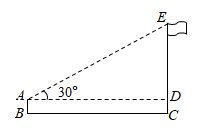

A、 $(15 \sqrt{3} + \frac{3}{2}) m$ B、 $5 \sqrt{3} m$ C、 $15 \sqrt{3} m$ D、 $(5 \sqrt{3} + \frac{3}{2}) m$

查看试题解析
10. 八年级学生去距学校10千米的博物馆参观，一部分学生骑自行车先走，过了20分钟后，其余学生乘汽车出发，结果他们同时到达，已知汽车的速度是骑车学生速度的2倍.设骑车学生的速度为x千米/小时，则所列方程正确的是（）

A、 $\frac{10}{x}$ - $\frac{10}{2 x}$ =20 B、 $\frac{10}{2 x}$ - $\frac{10}{x}$ =20 C、 $\frac{10}{x}$ - $\frac{10}{2 x}$ = $\frac{1}{3}$ D、 $\frac{10}{2 x} -$ $\frac{10}{x}$ = $\frac{1}{3}$

查看试题解析
11. 如图，正六边形 $A B C D E F$ 内接于 $⊙ O$ ，正六边形的周长是12，则 $⊙ O$ 的半径是（）

A、3 B、2 C、 $2 \sqrt{2}$ D、 $2 \sqrt{3}$

查看试题解析
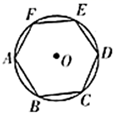12. 抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 的顶点为 $D (- 1 ， 2)$ ，与x轴的一个交点A在点 $(- 3 ， 0)$ 和 $(- 2 ， 0)$ 之间，其部分图象如图，则以下结论：① $b^{2} - 4 a c < 0$ ；②当 $x > - 1$ 时，y随x增大而减小；③ $a + b + c < 0$ ；④若方程 $a x^{2} + b x + c - m = 0$ 没有实数根，则 $m > 2$ ；⑤ $3 a + c < 0$ ，中正确的是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 如图，已知 $A B ∥ C D$ ，若 $∠ 1 = 37 ° 4 0^{'}$ ，则∠D的度数为．

查看试题解析
14. 把如图的图形折成正方体的盒子，折好后与“考”相对的字是．

查看试题解析
15. 若代数式 $\frac{x}{x - 2}$ 有意义，则实数x的取值范围是.

查看试题解析
16. 如图，⊙O中， $O C ⊥ A B$ ， $∠ A P C = 28 °$ ，则 $∠ B O C$ 的度数是．

查看试题解析
17. 化简： $\frac{(x + 2)^{2}}{x^{2} + 4 x + 4} - \frac{1}{x + 1} =$ ．

查看试题解析
18. 已知一次函数 $y = k x + b (k \neq 0)$ 的图象经过点 $A (- 3 ， 2)$ ，与x轴的交点为B，若 $O B = 4$ ，则这个一次函数的解析式为．

查看试题解析

三、解答题

19. 我校九年级163班所有学生参加体育测试，根据测试评分标准，将他们的成绩进行统计后分为A、B、C、D四等，并绘制成如图所示的条形统计图和扇形统计图（未完成），请结合图中所给信息解答下列问题：

(1)、九年级163班参加体育测试的学生共有多少人？

(2)、将条形统计图补充完整；

(3)、在扇形统计图中，求出等级C对应的圆心角的度数；

(4)、若规定达到A、B级为优秀，我校九年级共有学生850人，估计参加体育测试达到优秀标准的学生有多少人？

查看试题解析
20. 新中考理化科目更重视对学生独立思考、创新能力、分析和解决问题能力的考查．某校为培养学生动手和解决问题的能力，在期末考试中增设实验考试，规定每位学生必须在“A．观察凸透镜所成的像，B．用弹簧测力计测力，C．粗盐的提纯，D．过氧化氢分解制氧气”四个实验中抽取两个实验完成，假设小刚抽到每个实验的可能性相同．

(1)、若小刚从中任意抽取一个实验，求小刚抽到实验C的概率；

(2)、若小刚从中任意抽取两个实验，请用列表或画树状图（树状图也称树形图）中的一种方法，求小刚抽到的两个实验均为物理实验的概率．

查看试题解析
21. “绿水青山就是金山银山”的理念已融入人们的日常生活中，因此，越来越多的人喜欢骑自行车出行．某自行车店在销售某型号自行车时，以高出进价的50%标价．已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同．

(1)、求该型号自行车的进价和标价分别是多少元？

(2)、若该型号自行车的进价不变，按（1）中的标价出售，该店平均每月可售出51辆；若每辆自行车每降价20元，每月可多售出3辆，求该型号自行车降价多少元时，每月获利最大？最大利润是多少？

查看试题解析
22. 如图， $A B$ 是 $⊙ O$ 的直径，D是 $A B$ 延长线上的一点，点C在 $⊙ O$ 上， $B C = B D ， A E ⊥ C D$ 交 $D C$ 的延长线于点E， $A C$ 平分 $∠ B A E$ ．

(1)、求证： $C D$ 是 $⊙ O$ 的切线；

(2)、若 $C D = 6$ ，求 $⊙ O$ 的直径．

查看试题解析
23. 如图，在平行四边形ABCD中，以A为圆心，AB长为半径画弧交AD于点F；再分别以B、F为圆心，大于 $\frac{1}{2} B F$ 的相同长为半径画弧，两弧交于点P；连接AP并延长交BC于点E，连接EF，则四边形ABEF是菱形．

(1)、求证：四边形ABEF是菱形；

(2)、若菱形ABEF的周长为8， $A E = 2 \sqrt{3}$ ，求∠C的大小．

查看试题解析
24. 如图，抛物线y＝ax²+ $\frac{9}{4}$ x+c经过点A（﹣1，0）和点C （0，3）与x轴的另一交点为点B，点M是直线BC上一动点，过点M作MP∥y轴，交抛物线于点P.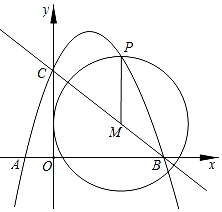

(1)、求该抛物线的解析式；

(2)、在抛物线上是否存在一点Q，使得△QCO是等边三角形？若存在，求出点Q的坐标；若不存在，请说明理由；

(3)、以M为圆心，MP为半径作⊙M，当⊙M与坐标轴相切时，求出⊙M的半径.

查看试题解析