云南省昆明市2022年中考校际联考数学试题(一模)
试卷更新日期:2022-07-06 类型:中考模拟
一、单选题
-
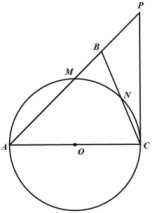
1. 第七次全国人口普查结果显示,我国人口受教育水平明显提高,具有大学文化程度的人数约为218360000,将218360000用科学记数法表示为( )A、0.21836×109 B、2.1386×107 C、21.836×107 D、2.1836×1082. 如图是一个由6个相同的正方体组成的立体图形,它的主视图是( )
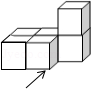 A、
A、 B、
B、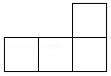 C、
C、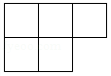 D、
D、 3. 下列运算错误的是( )A、 B、 C、 D、4. 如图, 是 的外角, , ,则 的度数为( )
3. 下列运算错误的是( )A、 B、 C、 D、4. 如图, 是 的外角, , ,则 的度数为( )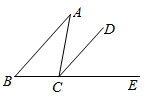 A、 B、 C、 D、5. 如图,已知AB=AC,AB=6,BC=4,分别以A、B两点为圆心,大于AB的长为半径画圆弧,两弧分别相交于点E、F,直线EF与AC相交于点D,则△BDC的周长为( )
A、 B、 C、 D、5. 如图,已知AB=AC,AB=6,BC=4,分别以A、B两点为圆心,大于AB的长为半径画圆弧,两弧分别相交于点E、F,直线EF与AC相交于点D,则△BDC的周长为( )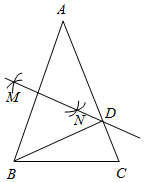 A、15 B、13 C、11 D、106. 如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还要添加一个条件是( )
A、15 B、13 C、11 D、106. 如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还要添加一个条件是( ) A、AB=DC B、∠A=∠D C、∠B=∠C D、AE=BF7. 某口罩生产车间接了一个60000个口罩的订单,由于任务紧急改进了生产工艺,效率为之前的 倍,完成订单后发现比工艺改进前还少用了10个小时,设工艺改进前每小时生产口罩 个,依据题意可得方程为( )A、 B、 C、 D、8. 关于x的方程(k﹣3)x2﹣4x+2=0有实数根,则k的取值范围是( )A、k≤5 B、k<5且k≠3 C、k≤5且k≠3 D、k≥5且k≠39. 按一定规律排列的单项式: , 第8个单项式是( )A、 B、 C、 D、10. 下列说法正确的个数是( )
A、AB=DC B、∠A=∠D C、∠B=∠C D、AE=BF7. 某口罩生产车间接了一个60000个口罩的订单,由于任务紧急改进了生产工艺,效率为之前的 倍,完成订单后发现比工艺改进前还少用了10个小时,设工艺改进前每小时生产口罩 个,依据题意可得方程为( )A、 B、 C、 D、8. 关于x的方程(k﹣3)x2﹣4x+2=0有实数根,则k的取值范围是( )A、k≤5 B、k<5且k≠3 C、k≤5且k≠3 D、k≥5且k≠39. 按一定规律排列的单项式: , 第8个单项式是( )A、 B、 C、 D、10. 下列说法正确的个数是( )①的相反数是2
②各边都相等的多边形叫正多边形
③了解一沓钞票中有没有假钞,应采用普查的形式
④一个多边形的内角和为720°,则这个多边形是六边形
⑤在平面直角坐标系中,点关于原点对称的点的坐标是
⑥与最接近的整数是4
A、2个 B、3个 C、4个 D、5个11. 如图,在矩形ABCD中,AB=4,BC= , E为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若tan∠BAF= , 则CE=( ) A、 B、 C、 D、12. 若关于x的一元一次不等式组的解集是 , 且a非正整数,则满足条件a的值的个数有( )个.A、1 B、2 C、3 D、4
A、 B、 C、 D、12. 若关于x的一元一次不等式组的解集是 , 且a非正整数,则满足条件a的值的个数有( )个.A、1 B、2 C、3 D、4二、填空题
-
13. 因式分解: .14. 若分式 的值为0,则x的值为.15. 如图,已知在⊙O 中,半径 OA= ,弦 AB=2,∠BAD=18°,OD 与AB 交于点 C,则∠ACO= 度.
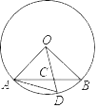 16. 如图,两个反比例函数 和 在第一象限内的图象分别是C1和C2 , 设点P在C1上,PA⊥x轴于点A,交C2于点B,则△POB的面积为 .
16. 如图,两个反比例函数 和 在第一象限内的图象分别是C1和C2 , 设点P在C1上,PA⊥x轴于点A,交C2于点B,则△POB的面积为 .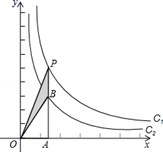 17.
17.如图,两同心圆的圆心为O,大圆的弦AB切小圆于P,两圆的半径分别为6、3,则图中阴影部分的面积是 .
 18. 在中,DE、MN分别垂直平分AB和AC,交BC于点D、M,若 , , 则 .
18. 在中,DE、MN分别垂直平分AB和AC,交BC于点D、M,若 , , 则 .三、解答题
-
19. 某校为了提高学生学习安全知识的积极性,举办了“安全第一”知识大赛,该校所有学生均参加初赛.初赛中,将安全知识设置为100分试卷,学生的分数均在50分以上,为了解学生对安全知识的掌握情况,学校随机抽取一部分学生的成绩进行统计分析,绘制了如下统计图表:
成绩x(分)
频数(人)
频率
2
0.04
10
0.2
14
b
a
0.32
8
0.16
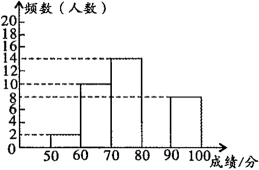
请根据统计图表提供的信息,解答下列问题:
(1)、本次抽样调查的样本容量是;(2)、;;(3)、补全频数分布直方图;(4)、若该校有2800名学生,初赛成绩不低于80分为优秀,则本次初赛达到优秀的学生大约有多少人?20. 小亮是个集邮爱好者,他收集了如图所示的四张纪念邮票(除正面内容不同外,其余均相同),现将四张邮票背面朝上,洗匀放好 (1)、小亮从中随机抽取一张邮票是“冬奥会吉祥物冰墩墩”的概率是(2)、小亮从中随机抽取一张邮票(不放回),再从余下的邮票中随机抽取一张,求抽到的两张邮票恰好是“冬奥会会徽”和“冬奥会吉祥物冰墩墩”的概率.(这四张邮票从左到右依次分别用字母A、B、C、D表示)21. 猕猴嬉戏是王屋山景区的一大特色,猕猴玩偶非常畅销.小李在某网店选中A,B两款猕猴玩偶,决定从该网店进货并销售.两款玩偶的进货价和销售价如下表:
(1)、小亮从中随机抽取一张邮票是“冬奥会吉祥物冰墩墩”的概率是(2)、小亮从中随机抽取一张邮票(不放回),再从余下的邮票中随机抽取一张,求抽到的两张邮票恰好是“冬奥会会徽”和“冬奥会吉祥物冰墩墩”的概率.(这四张邮票从左到右依次分别用字母A、B、C、D表示)21. 猕猴嬉戏是王屋山景区的一大特色,猕猴玩偶非常畅销.小李在某网店选中A,B两款猕猴玩偶,决定从该网店进货并销售.两款玩偶的进货价和销售价如下表:类别
价格
A款玩偶
B款玩偶
进货价(元/个)
40
30
销售价(元/个)
56
45
(1)、第一次小李用1100元购进了A,B两款玩偶共30个,求两款玩偶各购进多少个?(2)、第二次小李进货时,网店规定A款玩偶进货数量不得超过B款玩偶进货数量的一半.小李计划购进两款玩偶共30个,应如何设计进货方案才能获得最大利润,最大利润是多少?22. 如图,在平行四边形ABCD中,∠ABC的平分线BE交AD于点E,点F是BC边上的一点,且BF=AB,连接EF.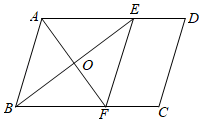 (1)、求证:四边形ABFE是菱形;(2)、连接AF,交BE于点O,若AB=5,BE+AF=14,求菱形ABFE的面积.
(1)、求证:四边形ABFE是菱形;(2)、连接AF,交BE于点O,若AB=5,BE+AF=14,求菱形ABFE的面积.